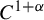Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Eynard-Bontemps, Hélène
and
Navas, Andrés
2025.
All, most, some? On diffeomorphisms of the interval that are distorted and/or conjugate to powers of themselves.
Proceedings of the Edinburgh Mathematical Society,
Vol. 68,
Issue. 3,
p.
909.