Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T01:06:34.460Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of periodic points near an isolated fixed point with Lefschetz index one and zero rotation for area preserving surface homeomorphisms

Published online by Cambridge University Press:  21 July 2015

JINGZHI YAN
JINGZHI YAN*
Affiliation:
Institut de Mathématiques de Jussieu-Paris Rive Gauche, 4 place Jussieu, 75252 Paris, France email jingzhi.yan@imj-prg.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 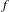$f$ be an orientation and area preserving diffeomorphism of an oriented surface 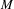$M$ with an isolated degenerate fixed point 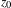$z_{0}$ with Lefschetz index one. Le Roux conjectured that 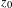$z_{0}$ is accumulated by periodic orbits. In this paper, we will approach Le Roux’s conjecture by proving that if 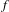$f$ is isotopic to the identity by an isotopy fixing 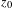$z_{0}$ and if the area of 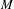$M$ is finite, then 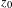$z_{0}$ is accumulated not only by periodic points, but also by periodic orbits in the measure sense. More precisely, the Dirac measure at 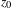$z_{0}$ is the limit in the weak-star topology of a sequence of invariant probability measures supported on periodic orbits. Our proof is purely topological. It works for homeomorphisms and is related to the notion of local rotation set.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 7 , October 2016 , pp. 2293 - 2333
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Birkhoff, G. D.. An extension of Poincaré’s last geometric theorem. Acta Math. 47(4) (1926), 297–311.Google Scholar
Boyland, P.. Rotation sets and monotone periodic orbits for annulus homeomorphisms. Comment. Math. Helv. 67(2) (1992), 203–213.CrossRefGoogle Scholar
Brouwer, L. E. J.. Beweis des ebenen Translationssatzes. Math. Ann. 72(1) (1912), 37–54.Google Scholar
Casson, A. J. and Bleiler, S. A.. Automorphisms of Surfaces after Nielsen and Thurston (London Mathematical Society Student Texts, 9) . Cambridge University Press, Cambridge, 1988.Google Scholar
Epstein, D. B. A.. Curves on 2-manifolds and isotopies. Acta Math. 115 (1966), 83–107.Google Scholar
Franks, J.. Generalizations of the Poincaré–Birkhoff theorem. Ann. of Math. (2) 128(1) (1988), 139–151.Google Scholar
Franks, J.. A new proof of the Brouwer plane translation theorem. Ergod. Th. & Dynam. Sys. 12(2) (1992), 217–226.Google Scholar
Franks, J.. Rotation vectors and fixed points of area preserving surface diffeomorphisms. Trans. Amer. Math. Soc. 348(7) (1996), 2637–2662.Google Scholar
Gambaudo, J.-M., Le Calvez, P. and Pécou, É.. Une généralisation d’un théorème de Naishul. C. R. Acad. Sci. Paris Sér. I Math. 323(4) (1996), 397–402.Google Scholar
Guillou, L.. Théorème de translation plane de Brouwer et généralisations du théorème de Poincaré–Birkhoff. Topology 33(2) (1994), 331–351.Google Scholar
Handel, M.. A fixed-point theorem for planar homeomorphisms. Topology 38(2) (1999), 235–264.Google Scholar
Jaulent, O.. Existence d’un feuilletage positivement transverse à un homéomorphisme de surface. Ann. Inst. Fourier (Grenoble) 64(4) (2014), 1441–1476.Google Scholar
Koropecki, A., Le Calvez, P. and Nassiri, M.. Prime ends rotation numbers and periodic points. Duke Math. J. 164 (2015), 403–472.Google Scholar
Le Calvez, P.. Une propriété dynamique des homéomorphismes du plan au voisinage d’un point fixe d’indice > 1. Topology 38(1) (1999), 23–35.Google Scholar
Le Calvez, P.. Dynamique des homéomorphismes du plan au voisinage d’un point fixe. Ann. Sci. Éc. Norm. Supér (4) 36(1) (2003), 139–171.Google Scholar
Le Calvez, P.. Une version feuilletée équivariante du théorème de translation de Brouwer. Publ. Math. Inst. Hautes Études Sci. 102 (2005), 1–98.Google Scholar
Le Calvez, P.. Pourquoi les points périodiques des homéomorphismes du plan tournent-ils autour de certains points fixes? Ann. Sci. Éc. Norm. Supér. (4) 41(1) (2008), 141–176.Google Scholar
Le Roux, F.. Homéomorphismes de surfaces: théorèmes de la fleur de Leau-Fatou et de la variété stable. Astérisque 292 (2004).Google Scholar
Le Roux, F.. A topological characterization of holomorphic parabolic germs in the plane. Fund. Math. 198(1) (2008), 77–94.Google Scholar
Le Roux, F.. L’ensemble de rotation autour d’un point fixe. Astérisque 350 (2013).Google Scholar
Matsumoto, S.. Types of fixed points of index one of surface homeomorphisms. Ergod. Th. & Dynam. Sys. 21(4) (2001), 1181–1211.Google Scholar
Mazzucchelli, M.. Symplectically degenerate maxima via generating functions. Math. Z. 275(3–4) (2013), 715–739.Google Scholar
McDuff, D. and Salamon, D.. Introduction to Symplectic Topology (Oxford Mathematical Monographs) , 2nd edn. Oxford University Press, Oxford, 1998.Google Scholar
Naĭshul′, V. A.. Topological invariants of analytic and area-preserving mappings and their application to analytic differential equations in C 2 and CP 2 . Tr. Mosk. Mat. Obs. 44 (1982), 235–245.Google Scholar
Pelikan, S. and Slaminka, E. E.. A bound for the fixed point index of area-preserving homeomorphisms of two-manifolds. Ergod. Th. & Dynam. Sys. 7(3) (1987), 463–479.Google Scholar
Ruelle, D.. Rotation numbers for diffeomorphisms and flows. Ann. Inst. H. Poincaré Phys. Théor. 42(1) (1985), 109–115.Google Scholar