Article contents
Extensions with shrinking fibers
Published online by Cambridge University Press: 24 April 2020
Abstract
We consider dynamical systems 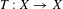 $T:X\rightarrow X$ that are extensions of a factor
$T:X\rightarrow X$ that are extensions of a factor 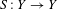 $S:Y\rightarrow Y$ through a projection
$S:Y\rightarrow Y$ through a projection 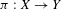 $\unicode[STIX]{x1D70B}:X\rightarrow Y$ with shrinking fibers, that is, such that
$\unicode[STIX]{x1D70B}:X\rightarrow Y$ with shrinking fibers, that is, such that  $T$ is uniformly continuous along fibers
$T$ is uniformly continuous along fibers 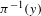 $\unicode[STIX]{x1D70B}^{-1}(y)$ and the diameter of iterate images of fibers
$\unicode[STIX]{x1D70B}^{-1}(y)$ and the diameter of iterate images of fibers 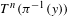 $T^{n}(\unicode[STIX]{x1D70B}^{-1}(y))$ uniformly go to zero as
$T^{n}(\unicode[STIX]{x1D70B}^{-1}(y))$ uniformly go to zero as 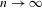 $n\rightarrow \infty$ . We prove that every
$n\rightarrow \infty$ . We prove that every  $S$ -invariant measure
$S$ -invariant measure 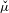 $\check{\unicode[STIX]{x1D707}}$ has a unique
$\check{\unicode[STIX]{x1D707}}$ has a unique  $T$ -invariant lift
$T$ -invariant lift  $\unicode[STIX]{x1D707}$ , and prove that many properties of
$\unicode[STIX]{x1D707}$ , and prove that many properties of 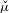 $\check{\unicode[STIX]{x1D707}}$ lift to
$\check{\unicode[STIX]{x1D707}}$ lift to  $\unicode[STIX]{x1D707}$ : ergodicity, weak and strong mixing, decay of correlations and statistical properties (possibly with weakening in the rates). The basic tool is a variation of the Wasserstein distance, obtained by constraining the optimal transportation paradigm to displacements along the fibers. We extend classical arguments to a general setting, enabling us to translate potentials and observables back and forth between
$\unicode[STIX]{x1D707}$ : ergodicity, weak and strong mixing, decay of correlations and statistical properties (possibly with weakening in the rates). The basic tool is a variation of the Wasserstein distance, obtained by constraining the optimal transportation paradigm to displacements along the fibers. We extend classical arguments to a general setting, enabling us to translate potentials and observables back and forth between 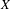 $X$ and
$X$ and  $Y$ .
$Y$ .
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s) 2020. Published by Cambridge University Press
References
- 6
- Cited by


