No CrossRef data available.
Article contents
A family of entire functions with Baker domains
Published online by Cambridge University Press: 01 April 2009
Abstract
In his paper [The iteration of polynomials and transcendental entire functions. J. Aust. Math. Soc. (Series A)30 (1981), 483–495], Baker proved that the function f defined by 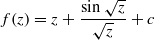 has a Baker domain for c sufficiently large. In this paper we use a novel method to prove that f has a Baker domain for all c>0. We also prove that there exists an open unbounded set contained in the Baker domain on which the orbits of points under f are asymptotically horizontal.
has a Baker domain for c sufficiently large. In this paper we use a novel method to prove that f has a Baker domain for all c>0. We also prove that there exists an open unbounded set contained in the Baker domain on which the orbits of points under f are asymptotically horizontal.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 2008
References
[1]Baker, I. N.. The iteration of polynomials and transcendental entire functions. J. Aust. Math. Soc. (Series A) 30 (1981), 483–495.CrossRefGoogle Scholar
[3]Bergweiler, W.. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151–188.CrossRefGoogle Scholar
[4]Fleischmann, D. S.. An entire function with a Baker domain and sparsely distributed singular values. Math. Proc. Cambridge Philos. Soc. 145 (2008), 227–241.CrossRefGoogle Scholar
[5]Morosawa, S.. An example of cyclic Baker domains. Mem. Fac. Sci. Kochi Univ. Ser. A Math. 20 (1999), 123–126.Google Scholar
[6]Morosawa, S., Nishimura, Y., Taniguchi, M. and Ueda, T.. Holomorphic Dynamics (Cambridge Studies in Advanced Mathematics, 66). Cambridge University Press, Cambridge, 1999.Google Scholar
[7]Rippon, P. J.. Baker domains. Transcendental Dynamics and Complex Analysis (Lecture Notes in Mathematics, 348). Cambridge University Press, Cambridge, 2008, pp. 371–395.CrossRefGoogle Scholar

