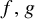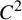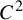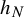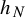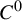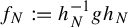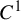1. Introduction
A
![]() $C^1$
map
$C^1$
map
![]() $f:S^1\rightarrow S^1$
is called expanding if
$f:S^1\rightarrow S^1$
is called expanding if
![]() $\min _{x\in S^1}|f'(x)|\geq \unicode{x3bb} _f>1$
. We call
$\min _{x\in S^1}|f'(x)|\geq \unicode{x3bb} _f>1$
. We call
![]() $\unicode{x3bb} _f$
the minimum expansion rate. Let
$\unicode{x3bb} _f$
the minimum expansion rate. Let
![]() $\operatorname {\mathrm {Exp}}^r(S^1)$
(
$\operatorname {\mathrm {Exp}}^r(S^1)$
(
![]() $r\geq 1$
) be the subspace of all
$r\geq 1$
) be the subspace of all
![]() $C^r$
uniformly expanding maps, and for
$C^r$
uniformly expanding maps, and for
![]() $\gamma>1$
, let
$\gamma>1$
, let
![]() $\operatorname {\mathrm {Exp}}^r_\gamma (S^1)$
be the space of all
$\operatorname {\mathrm {Exp}}^r_\gamma (S^1)$
be the space of all
![]() $C^r$
expanding maps whose minimum expansion rate is greater than or equal to
$C^r$
expanding maps whose minimum expansion rate is greater than or equal to
![]() $\gamma $
. Given any continuous map
$\gamma $
. Given any continuous map
![]() $f:S^1\rightarrow S^1$
, recall that the degree of f is defined to be value
$f:S^1\rightarrow S^1$
, recall that the degree of f is defined to be value
![]() $F(x+1)-F(x)$
, where
$F(x+1)-F(x)$
, where
![]() $F:\mathbb {R}\rightarrow \mathbb {R}$
is any lift of f. In addition to being well-defined independent of the choice of lift and the point
$F:\mathbb {R}\rightarrow \mathbb {R}$
is any lift of f. In addition to being well-defined independent of the choice of lift and the point
![]() $x\in S^1$
, it was proved by Shub in [Reference ShubShu69] that the degree is a complete topological conjugacy invariant for expanding maps on the circle.
$x\in S^1$
, it was proved by Shub in [Reference ShubShu69] that the degree is a complete topological conjugacy invariant for expanding maps on the circle.
Theorem 1.1. Let
![]() $f,g:S^1\rightarrow S^1$
be continuous expanding maps. Then there exists a homeomorphism
$f,g:S^1\rightarrow S^1$
be continuous expanding maps. Then there exists a homeomorphism
![]() $h:S^1\rightarrow S^1$
such that
$h:S^1\rightarrow S^1$
such that
![]() $h\circ f=g\circ h$
if and only if
$h\circ f=g\circ h$
if and only if
![]() $\deg (f)=\deg (g)$
.
$\deg (f)=\deg (g)$
.
It is easy to check that h is Hölder continuous, but there is an obstruction to h having higher regularity at the periodic orbits of f. By formally differentiating the conjugacy equation, it is clear that h will not be differentiable if
![]() $(f^n)'(x)\neq (g^n)'(h(x))$
for at least one periodic point
$(f^n)'(x)\neq (g^n)'(h(x))$
for at least one periodic point
![]() $x\in \operatorname {\mathrm {Fix}}(f^n)$
. As the next theorem shows, satisfying this obstruction at all periodic points is sufficient to conclude differentiability of h.
$x\in \operatorname {\mathrm {Fix}}(f^n)$
. As the next theorem shows, satisfying this obstruction at all periodic points is sufficient to conclude differentiability of h.
Theorem 1.2. Suppose
![]() $f,g:S^1\rightarrow S^1$
are
$f,g:S^1\rightarrow S^1$
are
![]() $C^{1+\alpha }$
(
$C^{1+\alpha }$
(
![]() $\alpha>0$
) expanding maps of the same degree, and fix a conjugacy h such that
$\alpha>0$
) expanding maps of the same degree, and fix a conjugacy h such that
![]() $h\circ f=g\circ h$
. Then, the map h is
$h\circ f=g\circ h$
. Then, the map h is
![]() $C^{1+\alpha }$
if and only if for every point
$C^{1+\alpha }$
if and only if for every point
![]() $p\in \operatorname {\mathrm {Fix}}(f^n)$
,
$p\in \operatorname {\mathrm {Fix}}(f^n)$
,
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
![]() $(f^n)'(p)=(g^n)'(h(p))$
.
$(f^n)'(p)=(g^n)'(h(p))$
.
While not directly stated in this form, a proof of Theorem 1.2 can be found from de la Llave [Reference de la LlaveLla92]. A closely related result is the theorem of Shub and Sullivan [Reference Shub and SullivanSS85], which proves that
![]() $C^r$
(
$C^r$
(
![]() $r\geq 2$
) expanding maps of the circle which are conjugated by an absolutely continuous homeomorphism
$r\geq 2$
) expanding maps of the circle which are conjugated by an absolutely continuous homeomorphism
![]() $h_1$
are in fact conjugated by a
$h_1$
are in fact conjugated by a
![]() $C^r$
diffeomorphism
$C^r$
diffeomorphism
![]() $h_2,$
but it may be that
$h_2,$
but it may be that
![]() $h_1\neq h_2$
. Martens and de Melo prove a more general version of Theorem 1.2 [Reference Martens and de MeloMM99, Corollary 2.9] applying to all
$h_1\neq h_2$
. Martens and de Melo prove a more general version of Theorem 1.2 [Reference Martens and de MeloMM99, Corollary 2.9] applying to all
![]() $C^r$
Markov maps in one dimension. In particular, the main theorem of [Reference Martens and de MeloMM99] applies to unimodal maps (with critical points) without wild and solenoidal attractors and establishes periodic data rigidity for these systems. The picture for general unimodal maps is more complicated: Moreira and Smania proved [Reference Moreira, Smania, Griffiths, Mather and SteinMS14] that unimodal maps with Cantor set attractor, such as Feigenbaum maps and Fibonacci maps with high order at the critical point, are always absolutely continuously conjugated, but not necessarily smoothly. Thus, Shub and Sullivan’s theorem does not carry over to these maps. It would be interesting to study finite data rigidity (Theorem 1.3 below) for unimodal and Markov maps as well.
$C^r$
Markov maps in one dimension. In particular, the main theorem of [Reference Martens and de MeloMM99] applies to unimodal maps (with critical points) without wild and solenoidal attractors and establishes periodic data rigidity for these systems. The picture for general unimodal maps is more complicated: Moreira and Smania proved [Reference Moreira, Smania, Griffiths, Mather and SteinMS14] that unimodal maps with Cantor set attractor, such as Feigenbaum maps and Fibonacci maps with high order at the critical point, are always absolutely continuously conjugated, but not necessarily smoothly. Thus, Shub and Sullivan’s theorem does not carry over to these maps. It would be interesting to study finite data rigidity (Theorem 1.3 below) for unimodal and Markov maps as well.
The goal of the present paper is to relax the conditions of Theorem 1.2 to hold at only finitely many periodic orbits, and then see how close f and g are to being smoothly conjugated.
Theorem 1.3. Let
![]() $\gamma>1$
be fixed and let
$\gamma>1$
be fixed and let
![]() $\mathcal {W}\subset \operatorname {\mathrm {Exp}}^2_\gamma (S^1)$
be a bounded subset. Then, there exist constants
$\mathcal {W}\subset \operatorname {\mathrm {Exp}}^2_\gamma (S^1)$
be a bounded subset. Then, there exist constants
![]() $K>0$
and
$K>0$
and
![]() $0<\unicode{x3bb} <1$
depending only on
$0<\unicode{x3bb} <1$
depending only on
![]() $\gamma>1$
and
$\gamma>1$
and
![]() $\mathcal {W}$
such that the following holds: if
$\mathcal {W}$
such that the following holds: if
![]() $f,g\in \mathcal {W}$
are conjugated by a homeomorphism h (
$f,g\in \mathcal {W}$
are conjugated by a homeomorphism h (
![]() $h\circ f=g\circ h$
) and if there exists
$h\circ f=g\circ h$
) and if there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $(f^N)'(p)=(g^N)'(h(p))$
for every
$(f^N)'(p)=(g^N)'(h(p))$
for every
![]() $p\in \operatorname {\mathrm {Fix}}(f^N)$
, then there exists a diffeomorphism
$p\in \operatorname {\mathrm {Fix}}(f^N)$
, then there exists a diffeomorphism
![]() ${h}_N\in C^2(S^1)$
such that
${h}_N\in C^2(S^1)$
such that
![]() $d_{C^0}(h,{h}_N)\leq K\unicode{x3bb} ^N$
. Moreover, for every
$d_{C^0}(h,{h}_N)\leq K\unicode{x3bb} ^N$
. Moreover, for every
![]() $0<\unicode{x3bb} ^{1/2}<\unicode{x3bb} _0<1$
, there exists a constant
$0<\unicode{x3bb} ^{1/2}<\unicode{x3bb} _0<1$
, there exists a constant
![]() $K'>0$
, such that if we let
$K'>0$
, such that if we let
![]() $f_N={h}_N^{-1}\circ g\circ {h}_N$
, then
$f_N={h}_N^{-1}\circ g\circ {h}_N$
, then
![]() $d_{C^1}(f,{f}_N)\leq K'\unicode{x3bb} _0^N$
.
$d_{C^1}(f,{f}_N)\leq K'\unicode{x3bb} _0^N$
.
Remark 1. The conjugacy
![]() $h_N$
we construct will not explicitly depend on the parameter N. Instead, the notation is meant to emphasize how much of the periodic data we can use for our estimates. A more descriptive notation would be
$h_N$
we construct will not explicitly depend on the parameter N. Instead, the notation is meant to emphasize how much of the periodic data we can use for our estimates. A more descriptive notation would be
![]() $h_{f,g,N}$
to emphasize the dependence on the expanding maps f and g. However, for the sake of brevity (as well as to avoid confusing notation for
$h_{f,g,N}$
to emphasize the dependence on the expanding maps f and g. However, for the sake of brevity (as well as to avoid confusing notation for
![]() $f_N$
), we will use the simplified notation
$f_N$
), we will use the simplified notation
![]() $h_N$
.
$h_N$
.
A key step in the proof of Theorem 1.3 is to prove an effective version of Bowen’s equidistribution theorem (see Theorem 2.2 below), which allows us to estimate the difference between h and
![]() ${h}_N$
in terms of the periodic orbits of order N. The convergence rate
${h}_N$
in terms of the periodic orbits of order N. The convergence rate
![]() $\unicode{x3bb} $
comes from the effective equidistribution rate and depends on the degree of the expanding maps and
$\unicode{x3bb} $
comes from the effective equidistribution rate and depends on the degree of the expanding maps and
![]() $\gamma $
. The proof of effective equidistribution is postponed until §3 and relies on the technique of Birkhoff cones for subshifts of finite type, which we recall in Appendix A. This technique is well known in the case of expanding maps; see for instance Baladi [Reference BaladiBal00].
$\gamma $
. The proof of effective equidistribution is postponed until §3 and relies on the technique of Birkhoff cones for subshifts of finite type, which we recall in Appendix A. This technique is well known in the case of expanding maps; see for instance Baladi [Reference BaladiBal00].
2. Finite data rigidity
The goal of this section is to generalize Theorem 1.2 to allow for the derivatives of f and g to agree only at finitely many periodic points. Of course, f and g will not be
![]() $C^1$
conjugate, but we can find a map
$C^1$
conjugate, but we can find a map
![]() $C^1$
close to f which is
$C^1$
close to f which is
![]() $C^1$
conjugate to g. Moreover, this new map converges exponentially to f as the number of periodic points that the derivatives agree on increases.
$C^1$
conjugate to g. Moreover, this new map converges exponentially to f as the number of periodic points that the derivatives agree on increases.
Definition 2.1. For a function
![]() $f\in C^k(S^1)$
,
$f\in C^k(S^1)$
,
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
![]() $|f|_{C^k}=\sup |D^kf|$
denote the
$|f|_{C^k}=\sup |D^kf|$
denote the
![]() $C^k$
seminorm. Let
$C^k$
seminorm. Let
![]() $\|f\|_{\infty }$
denote the supremum norm of f and let
$\|f\|_{\infty }$
denote the supremum norm of f and let
![]() $\|f\|_{C^k}=\|f\|_{\infty }+\sum _{i=1}^k|f|_{C^i}$
denote the
$\|f\|_{C^k}=\|f\|_{\infty }+\sum _{i=1}^k|f|_{C^i}$
denote the
![]() $C^k$
norm. If
$C^k$
norm. If
![]() $f:S^1\rightarrow S^1$
is
$f:S^1\rightarrow S^1$
is
![]() $\alpha $
-Hölder continuous (
$\alpha $
-Hölder continuous (
![]() $0<\alpha \leq 1$
), define
$0<\alpha \leq 1$
), define
 $$ \begin{align*}|f|_{\alpha}=\sup_{x\neq y}\frac{|f(x)-f(y)|}{|x-y|^\alpha} \end{align*} $$
$$ \begin{align*}|f|_{\alpha}=\sup_{x\neq y}\frac{|f(x)-f(y)|}{|x-y|^\alpha} \end{align*} $$
to be the Hölder seminorm and define
![]() $\|f\|_{\alpha }=\|f\|_{\infty }+|f|_{\mathrm {Lip}}$
to be the Hölder norm. For
$\|f\|_{\alpha }=\|f\|_{\infty }+|f|_{\mathrm {Lip}}$
to be the Hölder norm. For
![]() $\alpha =1$
, we get the Lipschitz seminorm and Lipschitz norm
$\alpha =1$
, we get the Lipschitz seminorm and Lipschitz norm
![]() $|\cdot |_{\mathrm {Lip}}$
and
$|\cdot |_{\mathrm {Lip}}$
and
![]() $\|\cdot \|_{\mathrm {Lip}}$
, respectively.
$\|\cdot \|_{\mathrm {Lip}}$
, respectively.
It well known that for a
![]() $C^{1+\alpha }$
expanding map f on a compact manifold M, there exists a unique invariant probability measure
$C^{1+\alpha }$
expanding map f on a compact manifold M, there exists a unique invariant probability measure
![]() $\mu _f$
which is absolutely continuous with respect to Lebesgue measure, whose density
$\mu _f$
which is absolutely continuous with respect to Lebesgue measure, whose density
![]() $\rho _f(x)$
is
$\rho _f(x)$
is
![]() $C^\alpha $
and strictly positive. See Baladi [Reference BaladiBal00] for full details. Moreover,
$C^\alpha $
and strictly positive. See Baladi [Reference BaladiBal00] for full details. Moreover,
![]() $\mu _f$
is the unique equilibrium state corresponding to the geometric potential
$\mu _f$
is the unique equilibrium state corresponding to the geometric potential
![]() $\psi _f=-\log (|f'(x)|)$
. For the uniformity claims of Theorem 1.3, it will be important to have uniform bounds on the densities
$\psi _f=-\log (|f'(x)|)$
. For the uniformity claims of Theorem 1.3, it will be important to have uniform bounds on the densities
![]() $\rho _f$
.
$\rho _f$
.
Lemma 2.1. Let
![]() $\mathcal {W}$
be a bounded set in
$\mathcal {W}$
be a bounded set in
![]() $\operatorname {\mathrm {Exp}}^2_\gamma (S^1)$
,
$\operatorname {\mathrm {Exp}}^2_\gamma (S^1)$
,
![]() $\gamma>1$
. Then, for every
$\gamma>1$
. Then, for every
![]() $0<\alpha <1$
, there exists
$0<\alpha <1$
, there exists
![]() $C>1$
such that for all
$C>1$
such that for all
![]() $f\in \mathcal {W}$
and every
$f\in \mathcal {W}$
and every
![]() $x\in S^1$
,
$x\in S^1$
,
![]() $C^{-1}\leq \rho _f(x)\leq C$
and
$C^{-1}\leq \rho _f(x)\leq C$
and
![]() $|\rho _f|_{C^\alpha }<C$
.
$|\rho _f|_{C^\alpha }<C$
.
Proof. We prove this using a Birkhoff cone argument. See Baladi [Reference BaladiBal00, §2.2] for details and Appendix A of the present paper for a similar argument for subshifts of finite type. For
![]() $L>0$
, consider the cone
$L>0$
, consider the cone
 $$ \begin{align*} \Lambda_L=\bigg\{\phi\in C^0(M) | \phi(x)>0, \frac{\phi(x)}{\phi(y)}\leq e^{Ld(x,y)^\alpha} \text{ for all } x,y\in S^1\bigg\}. \end{align*} $$
$$ \begin{align*} \Lambda_L=\bigg\{\phi\in C^0(M) | \phi(x)>0, \frac{\phi(x)}{\phi(y)}\leq e^{Ld(x,y)^\alpha} \text{ for all } x,y\in S^1\bigg\}. \end{align*} $$
Then, Baladi shows in [Reference BaladiBal00] that there exists
![]() $L>0$
depending only on
$L>0$
depending only on
![]() $\gamma>1$
and
$\gamma>1$
and
![]() $0<\alpha <1$
such that
$0<\alpha <1$
such that
![]() $\rho _f\in \Lambda _L$
. Since
$\rho _f\in \Lambda _L$
. Since
![]() $\rho _f$
is the smooth density of a probability measure, there exists a point
$\rho _f$
is the smooth density of a probability measure, there exists a point
![]() $y\in S^1$
such that
$y\in S^1$
such that
![]() $\rho _f(y)=1$
. Since
$\rho _f(y)=1$
. Since
![]() $\rho \in \Lambda _L$
, for any
$\rho \in \Lambda _L$
, for any
![]() $x\in S^1$
, we have
$x\in S^1$
, we have
and we likewise get the lower bound for
![]() $\rho (x)$
by swapping the roles of x and y. Finally, notice that
$\rho (x)$
by swapping the roles of x and y. Finally, notice that
![]() $\rho _f\in \Lambda _L$
is equivalent to
$\rho _f\in \Lambda _L$
is equivalent to
![]() $\log (\rho _f)\in C^\alpha (S^1)$
with
$\log (\rho _f)\in C^\alpha (S^1)$
with
![]() $|\log (\rho _f)|_\alpha \leq L$
. Then,
$|\log (\rho _f)|_\alpha \leq L$
. Then,
![]() $\rho _f=\exp (\log (\rho _f))$
and
$\rho _f=\exp (\log (\rho _f))$
and
Remark 2. One can prove uniform bounds on the densities without a Birkhoff cone argument by instead carefully going through the arguments of Sacksteder’s proof [Reference Sacksteder and VidalSac74] of the existence of invariant densities.
We are now ready to introduce the main technical tools needed to prove Theorem 1.3. We will use the notation
![]() $S_{f,n}\psi (x)$
to denote the nth ergodic sum of
$S_{f,n}\psi (x)$
to denote the nth ergodic sum of
![]() $\psi $
at the point x with respect to the dynamics of f:
$\psi $
at the point x with respect to the dynamics of f:
 $$ \begin{align*} S_{f,n}\psi(x)=\sum_{i=0}^{n-1}\psi(f^i(x)). \end{align*} $$
$$ \begin{align*} S_{f,n}\psi(x)=\sum_{i=0}^{n-1}\psi(f^i(x)). \end{align*} $$
Definition 2.2. Let
![]() $(X,f)$
be a dynamical system and
$(X,f)$
be a dynamical system and
![]() $\psi :X\rightarrow [0,\infty )$
a non-negative potential function. Whenever
$\psi :X\rightarrow [0,\infty )$
a non-negative potential function. Whenever
![]() $\operatorname {\mathrm {Fix}}(f^n)\not =\emptyset $
, we can define a measure
$\operatorname {\mathrm {Fix}}(f^n)\not =\emptyset $
, we can define a measure
![]() $\mu ^n_{f,\psi }$
by
$\mu ^n_{f,\psi }$
by
 $$ \begin{align*} \mu^n_{f,\psi}=\frac{1}{Z_n(f,\psi)}\sum_{x\in\operatorname{\mathrm{Fix}}(f^n)}e^{S_{f,n}\psi(x)}\delta_x, \end{align*} $$
$$ \begin{align*} \mu^n_{f,\psi}=\frac{1}{Z_n(f,\psi)}\sum_{x\in\operatorname{\mathrm{Fix}}(f^n)}e^{S_{f,n}\psi(x)}\delta_x, \end{align*} $$
where
 $$ \begin{align*} Z_n(f,\psi)=\sum_{x\in\operatorname{\mathrm{Fix}}(f^n)}e^{S_{f,n}\psi(x)} \end{align*} $$
$$ \begin{align*} Z_n(f,\psi)=\sum_{x\in\operatorname{\mathrm{Fix}}(f^n)}e^{S_{f,n}\psi(x)} \end{align*} $$
is a normalization constant so that
![]() $\mu ^n_{f,\psi }$
is a probability measure. We call
$\mu ^n_{f,\psi }$
is a probability measure. We call
![]() $\mu ^n_{f,\psi }$
the nth weighted discrete measure associated to the dynamics of f and the potential
$\mu ^n_{f,\psi }$
the nth weighted discrete measure associated to the dynamics of f and the potential
![]() $\psi $
.
$\psi $
.
The measure
![]() $\mu ^n_{f,\psi }$
depends on three ingredients: the length n of periodic orbits under consideration, the dynamical system
$\mu ^n_{f,\psi }$
depends on three ingredients: the length n of periodic orbits under consideration, the dynamical system
![]() $f:X\rightarrow X$
, and the potential function
$f:X\rightarrow X$
, and the potential function
![]() $\phi :X\rightarrow [0,\infty )$
. In our setting, we will be considering a smooth expanding map
$\phi :X\rightarrow [0,\infty )$
. In our setting, we will be considering a smooth expanding map
![]() $f:S^1\rightarrow S^1$
together with the associated geometric potential
$f:S^1\rightarrow S^1$
together with the associated geometric potential
![]() $\psi _f(x)=-\log (|f'(x)|)$
. When this is the case, since the potential depends on the dynamics, we will use the more compact notation
$\psi _f(x)=-\log (|f'(x)|)$
. When this is the case, since the potential depends on the dynamics, we will use the more compact notation
![]() $\mu ^n_f$
in place of
$\mu ^n_f$
in place of
![]() $\mu ^n_{f,\psi _f}$
.
$\mu ^n_{f,\psi _f}$
.
Let us recall the following theorem of Bowen [Reference BowenBow74].
Theorem 2.2. (Bowen’s equidistribution theorem)
Let
![]() $(X,d)$
be a compact metric space,
$(X,d)$
be a compact metric space,
![]() $f:X\rightarrow X$
an expansive homeomorphism with the specification property, and
$f:X\rightarrow X$
an expansive homeomorphism with the specification property, and
![]() $\psi \in C^f(X)$
. Then, there exists a unique equilibrium state
$\psi \in C^f(X)$
. Then, there exists a unique equilibrium state
![]() $\mu _{\psi }\in \mathcal {M}(f)$
given by
$\mu _{\psi }\in \mathcal {M}(f)$
given by
where the limit converges in the weak
![]() $^*$
-topology.
$^*$
-topology.
Remark 3. Theorem 2.2 is sufficient for proving Theorem 1.2 (though Bowen’s theorem is stated for invertible systems, the same result is true for uniformly expanding maps on the circle with essentially the same proof; see also Theorem 2.3 below). Indeed, from the assumption on periodic data, it follows that
![]() $\mu _f^n=h^*\mu ^n_g$
for all
$\mu _f^n=h^*\mu ^n_g$
for all
![]() $n\in \mathbb {N}$
, where
$n\in \mathbb {N}$
, where
![]() $h^*\mu _g$
denotes the pullback measure by h. Then, taking weak
$h^*\mu _g$
denotes the pullback measure by h. Then, taking weak
![]() $^*$
-limits and using Theorem 2.2, we conclude that
$^*$
-limits and using Theorem 2.2, we conclude that
![]() $\mu _f=h^*\mu _g$
. Defining the functions
$\mu _f=h^*\mu _g$
. Defining the functions
and integrating
![]() $\mu _f=h^*\mu _g$
from
$\mu _f=h^*\mu _g$
from
![]() $0$
to x, we find that
$0$
to x, we find that
![]() $I_f(x)=I_g(h(x))$
or
$I_f(x)=I_g(h(x))$
or
Equation (2.1) provides us with insight as to how we should define
![]() $h_N$
in the proof of Theorem 1.3.
$h_N$
in the proof of Theorem 1.3.
To estimate
![]() $d_{C^0}(h,h_N)$
in Theorem 1.3, we will need the following effective version of Theorem 2.2.
$d_{C^0}(h,h_N)$
in Theorem 1.3, we will need the following effective version of Theorem 2.2.
Theorem 2.3. (Effective equidistribution)
Let
![]() $\mathcal {W}$
be as bounded set in
$\mathcal {W}$
be as bounded set in
![]() $\operatorname {\mathrm {Exp}}^2_\gamma (S^1)$
,
$\operatorname {\mathrm {Exp}}^2_\gamma (S^1)$
,
![]() $\gamma>1$
. Let
$\gamma>1$
. Let
![]() $f\in \mathcal {W}$
,
$f\in \mathcal {W}$
,
![]() $\psi _f:S^1\rightarrow \mathbb {C}$
be the geometric potential of f with unique equilibrium state
$\psi _f:S^1\rightarrow \mathbb {C}$
be the geometric potential of f with unique equilibrium state
![]() $\mu _f$
, and let
$\mu _f$
, and let
![]() $\mu ^N_{f}$
be the Nth weighted discrete measure associated to f and
$\mu ^N_{f}$
be the Nth weighted discrete measure associated to f and
![]() $\psi _f$
. Then, there exist constants
$\psi _f$
. Then, there exist constants
![]() $C'>0$
and
$C'>0$
and
![]() $0<\tau <1$
, depending only on
$0<\tau <1$
, depending only on
![]() $\mathcal {W}$
, such that for every Lipschitz function
$\mathcal {W}$
, such that for every Lipschitz function
![]() $\phi :S^1\rightarrow \mathbb {C}$
, we have
$\phi :S^1\rightarrow \mathbb {C}$
, we have
 $$ \begin{align} \bigg|\!\int\phi \,d\mu_f-\int\phi \,d\mu_f^N\bigg|\leq C'\|\phi\|_{\mathrm{Lip}}\tau^N. \end{align} $$
$$ \begin{align} \bigg|\!\int\phi \,d\mu_f-\int\phi \,d\mu_f^N\bigg|\leq C'\|\phi\|_{\mathrm{Lip}}\tau^N. \end{align} $$
We will defer the proof of Theorem 2.3 to §3. See Kadyrov [Reference KadyrovKad16, Theorem 1.5] for a more general result for the measure of maximal entropy of a subshift of finite type, and Rühr [Reference RührRüh21] for a version applying to equilibrium states of countable state shifts.
To prove Theorem 1.3, we will need to apply a version of Theorem 2.3 to the characteristic functions
![]() $\chi _{[0,x]}$
for every
$\chi _{[0,x]}$
for every
![]() $x\in S^1$
.
$x\in S^1$
.
Lemma 2.4. There exist constants
![]() $K>0$
and
$K>0$
and
![]() $0<\unicode{x3bb} <1$
such that for every
$0<\unicode{x3bb} <1$
such that for every
![]() $f\in \mathcal {W}$
, every
$f\in \mathcal {W}$
, every
![]() $x\in S^1$
, and every
$x\in S^1$
, and every
![]() $N\in \mathbb {N}$
,
$N\in \mathbb {N}$
,
 $$ \begin{align} \bigg|\!\int_0^x\,d\mu_f-\int_0^x\,d\mu_f^N\bigg|\leq K\unicode{x3bb}^N. \end{align} $$
$$ \begin{align} \bigg|\!\int_0^x\,d\mu_f-\int_0^x\,d\mu_f^N\bigg|\leq K\unicode{x3bb}^N. \end{align} $$
Here and throughout the paper, we write
![]() $\int _0^x\,d\mu _f^N$
as shorthand notation for
$\int _0^x\,d\mu _f^N$
as shorthand notation for
![]() $\int \chi _{[0,x]}\,d\mu _f^N=\mu _f^N([0,x])$
.
$\int \chi _{[0,x]}\,d\mu _f^N=\mu _f^N([0,x])$
.
Proof. We would like to apply Theorem 2.3 but cannot do so directly since the characteristic function
![]() $\chi _{[0,x]}$
is not Lipschitz continuous. Instead, we will approximate
$\chi _{[0,x]}$
is not Lipschitz continuous. Instead, we will approximate
![]() $\chi _{[0,x]}$
by a Lipschitz function
$\chi _{[0,x]}$
by a Lipschitz function
![]() $\phi _x$
and show that the effective equidistribution in equation (2.2) of
$\phi _x$
and show that the effective equidistribution in equation (2.2) of
![]() $\phi _x$
can be passed on to
$\phi _x$
can be passed on to
![]() $\chi _{[0,x]}$
, albeit with a slower rate of convergence. To find an appropriate choice of
$\chi _{[0,x]}$
, albeit with a slower rate of convergence. To find an appropriate choice of
![]() $\phi _x$
, we will construct a one-parameter family of Lipschitz functions
$\phi _x$
, we will construct a one-parameter family of Lipschitz functions
![]() $\phi _x^s$
for
$\phi _x^s$
for
![]() $s\in [0,\tau ^{N/2}]$
, where
$s\in [0,\tau ^{N/2}]$
, where
![]() $\tau $
is as in Theorem 2.3, satisfying the following properties:
$\tau $
is as in Theorem 2.3, satisfying the following properties:
-
(1) the family
 $\phi ^s_{x}$
varies continuously with s in the
$\phi ^s_{x}$
varies continuously with s in the
 $C^0$
-topology;
$C^0$
-topology; -
(2)
 $\phi ^0_{x}\leq \chi _{[0,x]}$
and
$\phi ^0_{x}\leq \chi _{[0,x]}$
and
 $\phi ^{\tau ^{N/2}}_{x}\geq \chi _{[0,x]}$
;
$\phi ^{\tau ^{N/2}}_{x}\geq \chi _{[0,x]}$
; -
(3) for every
 $s\in [0,\tau ^{N/2}]$
,
$s\in [0,\tau ^{N/2}]$
,
 $|\phi ^s_{x}|_{\mathrm {Lip}}\leq \tau ^{-N/2}$
;
$|\phi ^s_{x}|_{\mathrm {Lip}}\leq \tau ^{-N/2}$
; -
(4) for every
 $s\in [0,\tau ^{N/2}]$
,
$s\in [0,\tau ^{N/2}]$
,
 $|\phi ^s_{x}-\chi _{[0,x]}|=0$
except on a set
$|\phi ^s_{x}-\chi _{[0,x]}|=0$
except on a set
 $\Omega _N$
of Lebesgue measure
$\Omega _N$
of Lebesgue measure
 $m(\Omega _N)\leq 2\tau ^{N/2}$
.
$m(\Omega _N)\leq 2\tau ^{N/2}$
.
The definition of the families
![]() $\phi ^s_x$
depends on the point
$\phi ^s_x$
depends on the point
![]() $x\in S^1$
, though the typical graph of the functions are all similar and illustrated in Figure 1. We split the construction of the
$x\in S^1$
, though the typical graph of the functions are all similar and illustrated in Figure 1. We split the construction of the
![]() $\phi _x^s$
into three general cases.
$\phi _x^s$
into three general cases.

Figure 1 The family
![]() $\phi ^s_x$
at
$\phi ^s_x$
at
![]() $s=0$
(below
$s=0$
(below
![]() $\chi_{[0,x]}$
) and
$\chi_{[0,x]}$
) and
![]() $s=\tau^{N/2}$
(above
$s=\tau^{N/2}$
(above
![]() $\chi_{[0,x]}$
).
$\chi_{[0,x]}$
).
Case 1. Assume that
![]() $2\tau ^{N/2}\leq x\leq 1-2\tau ^{N/2}$
: Fix
$2\tau ^{N/2}\leq x\leq 1-2\tau ^{N/2}$
: Fix
![]() $2\tau ^{N/2}\leq x\leq 1-2\tau ^{N/2}$
and define a family of continuous functions as follows:
$2\tau ^{N/2}\leq x\leq 1-2\tau ^{N/2}$
and define a family of continuous functions as follows:
 $$ \begin{align*} \phi_x^s(y)= \begin{cases} \tau^{-N/2}(y+s), & -s\leq y\leq \tau^{N/2}-s, \\ 1, & \tau^{N/2}-s\leq y\leq s-(\tau^{N/2}-x), \\ -\tau^{-N/2}(y-s)+\tau^{-N/2}x, & s-(\tau^{N/2}-x)\leq y\leq x+s, \\ 0, & x+s\leq y\leq 1-s. \\ \end{cases} \end{align*} $$
$$ \begin{align*} \phi_x^s(y)= \begin{cases} \tau^{-N/2}(y+s), & -s\leq y\leq \tau^{N/2}-s, \\ 1, & \tau^{N/2}-s\leq y\leq s-(\tau^{N/2}-x), \\ -\tau^{-N/2}(y-s)+\tau^{-N/2}x, & s-(\tau^{N/2}-x)\leq y\leq x+s, \\ 0, & x+s\leq y\leq 1-s. \\ \end{cases} \end{align*} $$
It can be easily shown that the above family has the stated properties. Next, we estimate
 $$ \begin{align} &\bigg|\!\int_0^x\,d\mu_f-\int_0^x\,d\mu_f^N\bigg|\nonumber\\&\quad\leq \bigg|\!\int_0^xd\mu_f-\int\phi_x^s\,d\mu_f\bigg| +\bigg|\!\int\phi_x^s\,d\mu_f-\int\phi_x^s\,d\mu_f^N\bigg| +\bigg|\!\int\phi_x^s\,d\mu_f^N-\int_0^x\,d\mu_f^N\bigg|. \end{align} $$
$$ \begin{align} &\bigg|\!\int_0^x\,d\mu_f-\int_0^x\,d\mu_f^N\bigg|\nonumber\\&\quad\leq \bigg|\!\int_0^xd\mu_f-\int\phi_x^s\,d\mu_f\bigg| +\bigg|\!\int\phi_x^s\,d\mu_f-\int\phi_x^s\,d\mu_f^N\bigg| +\bigg|\!\int\phi_x^s\,d\mu_f^N-\int_0^x\,d\mu_f^N\bigg|. \end{align} $$
Let us consider each term on the right side of equation (2.4) separately. The first term can be rewritten as
 $$ \begin{align*} \bigg|\!\int_0^x\,d\mu_f-\int\phi_x^s\,d\mu_f\bigg|= \bigg|\!\int(\chi_{[0,x]}(y)-\phi_x^s(y))\rho_f(y)\,dy\bigg|. \end{align*} $$
$$ \begin{align*} \bigg|\!\int_0^x\,d\mu_f-\int\phi_x^s\,d\mu_f\bigg|= \bigg|\!\int(\chi_{[0,x]}(y)-\phi_x^s(y))\rho_f(y)\,dy\bigg|. \end{align*} $$
By property (4) of the family
![]() $\phi _x^s$
,
$\phi _x^s$
,
![]() $|\chi _{[0,x]}(y)-\phi _x^s(y)|=0$
except on a set of Lebesgue measure less than
$|\chi _{[0,x]}(y)-\phi _x^s(y)|=0$
except on a set of Lebesgue measure less than
![]() $2\tau ^{N/2}$
(depending on s), and is otherwise bounded above by
$2\tau ^{N/2}$
(depending on s), and is otherwise bounded above by
![]() $1$
. Furthermore, by Lemma 2.1, there exists
$1$
. Furthermore, by Lemma 2.1, there exists
![]() $C>1$
such that the density
$C>1$
such that the density
![]() $\rho _f$
of
$\rho _f$
of
![]() $\mu _f$
is bounded above by C. Hence,
$\mu _f$
is bounded above by C. Hence,
![]() $|\chi _{[0,x]}(y)-\phi _x^s(y)|=0$
except on a set of
$|\chi _{[0,x]}(y)-\phi _x^s(y)|=0$
except on a set of
![]() $\mu _f$
-measure less than
$\mu _f$
-measure less than
![]() $2C\tau ^{N/2}$
, and is otherwise bounded above by
$2C\tau ^{N/2}$
, and is otherwise bounded above by
![]() $1$
. Therefore,
$1$
. Therefore,
 $$ \begin{align*} \bigg|\!\int(\chi_{[0,x]}(y)-\phi_x^s(y))\rho(y)\,dy\bigg|\leq 2C\tau^{N/2}. \end{align*} $$
$$ \begin{align*} \bigg|\!\int(\chi_{[0,x]}(y)-\phi_x^s(y))\rho(y)\,dy\bigg|\leq 2C\tau^{N/2}. \end{align*} $$
For the second term on the right side of equation (2.4), we observe that by property (3), we have
![]() $\|\phi _x^s\|_{\mathrm {Lip}}=1+\tau ^{-N/2}$
. We can therefore apply Theorem 2.3 to find
$\|\phi _x^s\|_{\mathrm {Lip}}=1+\tau ^{-N/2}$
. We can therefore apply Theorem 2.3 to find
 $$ \begin{align*}\bigg|\!\int\phi_x^s\,d\mu_f-\int\phi_x^s\,d\mu_f^N\bigg|\leq C(1+\tau^{-N/2})\tau^N=C(\tau^N+\tau^{N/2})\leq C\tau^{N/2}.\end{align*} $$
$$ \begin{align*}\bigg|\!\int\phi_x^s\,d\mu_f-\int\phi_x^s\,d\mu_f^N\bigg|\leq C(1+\tau^{-N/2})\tau^N=C(\tau^N+\tau^{N/2})\leq C\tau^{N/2}.\end{align*} $$
We claim that the final term on the right side of equation (2.4) is zero for some choice of s. Define
Then by property (2), since
![]() $\Phi (0)$
is the integral of a strictly negative function with respect to a positive measure, we have
$\Phi (0)$
is the integral of a strictly negative function with respect to a positive measure, we have
![]() $\Phi (0)\leq 0$
, and likewise
$\Phi (0)\leq 0$
, and likewise
![]() $\Phi (\tau ^{N/2})\geq 0$
. We claim that
$\Phi (\tau ^{N/2})\geq 0$
. We claim that
![]() $\Phi (s)$
is a continuous function of s. Indeed, by property (1), fixing
$\Phi (s)$
is a continuous function of s. Indeed, by property (1), fixing
![]() $\varepsilon>0$
, we can find a
$\varepsilon>0$
, we can find a
![]() $\delta>0$
such that if
$\delta>0$
such that if
![]() $|s_1-s_2|<\delta $
, then
$|s_1-s_2|<\delta $
, then
![]() $\|\phi _x^{s_1}-\phi _x^{s_2}\|_{\infty }<\varepsilon $
. Then,
$\|\phi _x^{s_1}-\phi _x^{s_2}\|_{\infty }<\varepsilon $
. Then,
 $$ \begin{align*} |\Phi(s_1)-\Phi(s_2)|=\bigg|\!\int(\phi_x^{s_1}-\phi_x^{s_2})\,d\mu_f^N\bigg|<\varepsilon\mu_f^N(0,1)=\varepsilon. \end{align*} $$
$$ \begin{align*} |\Phi(s_1)-\Phi(s_2)|=\bigg|\!\int(\phi_x^{s_1}-\phi_x^{s_2})\,d\mu_f^N\bigg|<\varepsilon\mu_f^N(0,1)=\varepsilon. \end{align*} $$
By the intermediate value theorem, we can therefore choose some
![]() $0<s<\tau ^{N/2}$
so that
$0<s<\tau ^{N/2}$
so that
![]() $\Phi (s)=0$
. Therefore, combining these three bounds, we have the following bound on equation (2.4):
$\Phi (s)=0$
. Therefore, combining these three bounds, we have the following bound on equation (2.4):
 $$ \begin{align*} \bigg|\!\int_0^x \,d\mu_f-\int_0^x \,d\mu_f^N \bigg|\leq 2C\tau^{N/2}+C\tau^{N/2}+0= K\tau^{N/2}, \end{align*} $$
$$ \begin{align*} \bigg|\!\int_0^x \,d\mu_f-\int_0^x \,d\mu_f^N \bigg|\leq 2C\tau^{N/2}+C\tau^{N/2}+0= K\tau^{N/2}, \end{align*} $$
which is exactly equation (2.3), with
![]() $\unicode{x3bb} =\tau ^{1/2}$
.
$\unicode{x3bb} =\tau ^{1/2}$
.
Case 2. Assume that
![]() $x>1-2\tau ^{N/2}$
: The proof is nearly identical as in Case 1, but we use a slightly different family of Lipschitz functions:
$x>1-2\tau ^{N/2}$
: The proof is nearly identical as in Case 1, but we use a slightly different family of Lipschitz functions:
 $$ \begin{align*} \phi_x^s(y)= \begin{cases} \tau^{-N/2}(y+s), & -s\leq y\leq \tau^{N/2}-s, \\ 1, & \tau^{N/2}-s\leq y\leq s-(\tau^{N/2}-x), \\ -\tau^{-N/2}(y-s)+\tau^{-N/2}x, & s-(\tau^{N/2}-x)\leq y\leq x+s, \\ 0, & x+s\leq y\leq 1-s, \\ \end{cases} \end{align*} $$
$$ \begin{align*} \phi_x^s(y)= \begin{cases} \tau^{-N/2}(y+s), & -s\leq y\leq \tau^{N/2}-s, \\ 1, & \tau^{N/2}-s\leq y\leq s-(\tau^{N/2}-x), \\ -\tau^{-N/2}(y-s)+\tau^{-N/2}x, & s-(\tau^{N/2}-x)\leq y\leq x+s, \\ 0, & x+s\leq y\leq 1-s, \\ \end{cases} \end{align*} $$
for
![]() $0\leq s\leq ({1+x})/{2}$
, and
$0\leq s\leq ({1+x})/{2}$
, and
 $$ \begin{align*} \phi_x^s(y)= \begin{cases} 1, & \tau^{N/2}-s\leq y\leq s-(\tau^{N/2}-x), \\ -\tau^{-N/2}(y-s)+\tau^{-N/2}x, & s-(\tau^{N/2}-x)\leq y\leq \dfrac{1+x}{2}, \\ \tau^{-N/2}(y-1+s), & \dfrac{1+x}{2}\leq y\leq 1-s, \\ \end{cases} \end{align*} $$
$$ \begin{align*} \phi_x^s(y)= \begin{cases} 1, & \tau^{N/2}-s\leq y\leq s-(\tau^{N/2}-x), \\ -\tau^{-N/2}(y-s)+\tau^{-N/2}x, & s-(\tau^{N/2}-x)\leq y\leq \dfrac{1+x}{2}, \\ \tau^{-N/2}(y-1+s), & \dfrac{1+x}{2}\leq y\leq 1-s, \\ \end{cases} \end{align*} $$
for
![]() $({1+x})/{2}\leq s\leq \tau ^{N/2}$
. The remainder of the proof is identical to Case 1.
$({1+x})/{2}\leq s\leq \tau ^{N/2}$
. The remainder of the proof is identical to Case 1.
Case 3. Assume that
![]() $x\leq 2\tau ^{N/2}$
: The proof is again identical to Case 1 but with the following family:
$x\leq 2\tau ^{N/2}$
: The proof is again identical to Case 1 but with the following family:
 $$ \begin{align*} \phi_x^s(y)= \begin{cases} \tau^{-N/2}(y+s), & -s\leq y\leq \dfrac{x}{2}, \\ -\tau^{-N/2}(y-s)+\tau^{-N/2}x, & \dfrac{x}{2}\leq y\leq s, \\ 0, & s\leq y\leq 1-s, \\ \end{cases} \end{align*} $$
$$ \begin{align*} \phi_x^s(y)= \begin{cases} \tau^{-N/2}(y+s), & -s\leq y\leq \dfrac{x}{2}, \\ -\tau^{-N/2}(y-s)+\tau^{-N/2}x, & \dfrac{x}{2}\leq y\leq s, \\ 0, & s\leq y\leq 1-s, \\ \end{cases} \end{align*} $$
for
![]() $0\leq s\leq \tau ^{N/2}-{x}/{2}$
, and
$0\leq s\leq \tau ^{N/2}-{x}/{2}$
, and
 $$ \begin{align*} \phi_x^s(y)= \begin{cases} \tau^{-N/2}(y+s,) & -s\leq y\leq \tau^{N/2}-s, \\ 1, & \tau^{N/2}-s\leq y\leq s+\tau^Nx-\tau^{-N/2},\\ -\tau^{-N/2}(y-s)+\tau^{-N/2}x, & s+\tau^Nx-\tau^{-N/2}\leq y\leq s, \\ 0, & s\leq y\leq 1-s, \\ \end{cases} \end{align*} $$
$$ \begin{align*} \phi_x^s(y)= \begin{cases} \tau^{-N/2}(y+s,) & -s\leq y\leq \tau^{N/2}-s, \\ 1, & \tau^{N/2}-s\leq y\leq s+\tau^Nx-\tau^{-N/2},\\ -\tau^{-N/2}(y-s)+\tau^{-N/2}x, & s+\tau^Nx-\tau^{-N/2}\leq y\leq s, \\ 0, & s\leq y\leq 1-s, \\ \end{cases} \end{align*} $$
for
![]() $\tau ^{N/2}-{x}/{2}\leq s\leq \tau ^{N/2}$
. Observe that for every
$\tau ^{N/2}-{x}/{2}\leq s\leq \tau ^{N/2}$
. Observe that for every
![]() $0\leq s\leq \tau ^{N/2}$
,
$0\leq s\leq \tau ^{N/2}$
,
![]() $\|\phi _x^s\|_{\infty }\leq 1$
, so that
$\|\phi _x^s\|_{\infty }\leq 1$
, so that
![]() $\|\phi _x^s\|_{\mathrm {Lip}}\leq 1+ \tau ^{-N/2}$
, so the remainder of the argument in Case 1 carries over verbatim.
$\|\phi _x^s\|_{\mathrm {Lip}}\leq 1+ \tau ^{-N/2}$
, so the remainder of the argument in Case 1 carries over verbatim.
Proof of Theorem 1.3
We begin by recalling that when we have matching of all periodic data, the conjugacy h could be expressed as the smooth composition in equation (2.1). Observe that the latter expression
![]() $I_g^{-1}\circ I_f$
is a well-defined
$I_g^{-1}\circ I_f$
is a well-defined
![]() $C^{1+\alpha }$
function without any hypotheses on the periodic data. For this reason, we define
$C^{1+\alpha }$
function without any hypotheses on the periodic data. For this reason, we define
![]() $h_N:=I_g^{-1}\circ I_f$
.
$h_N:=I_g^{-1}\circ I_f$
.
Observe that since
![]() $(f^N)'(p)=(g^N)'(h(p))$
for every
$(f^N)'(p)=(g^N)'(h(p))$
for every
![]() $p\in \operatorname {\mathrm {Fix}}(f^N)$
, we have that
$p\in \operatorname {\mathrm {Fix}}(f^N)$
, we have that
![]() $\mu _f^N=h^*\mu _g^N$
:
$\mu _f^N=h^*\mu _g^N$
:
 $$ \begin{align*} &h^*\bigg(\frac{1}{Z_N(\psi_g)}\sum_{x\in\operatorname{\mathrm{Fix}}(g^N)}\exp(S_N\psi_g(x))\delta_x\bigg)\\&\quad= \frac{1}{Z_N(\psi_g)}\sum_{x\in\operatorname{\mathrm{Fix}}(g^N)}\exp(S_N\psi_g(h(h^{-1}x)))\delta_{h^{-1}(x)}\\ &\quad=\frac{1}{Z_N(\psi_f)}\sum_{y\in\operatorname{\mathrm{Fix}}(f^N)}\exp(S_N\psi_f(y))\delta_y=\mu_f^N. \end{align*} $$
$$ \begin{align*} &h^*\bigg(\frac{1}{Z_N(\psi_g)}\sum_{x\in\operatorname{\mathrm{Fix}}(g^N)}\exp(S_N\psi_g(x))\delta_x\bigg)\\&\quad= \frac{1}{Z_N(\psi_g)}\sum_{x\in\operatorname{\mathrm{Fix}}(g^N)}\exp(S_N\psi_g(h(h^{-1}x)))\delta_{h^{-1}(x)}\\ &\quad=\frac{1}{Z_N(\psi_f)}\sum_{y\in\operatorname{\mathrm{Fix}}(f^N)}\exp(S_N\psi_f(y))\delta_y=\mu_f^N. \end{align*} $$
We now calculate
 $$ \begin{align*}&|{h}_N(x)-h(x)|\\&\quad=|I_g^{-1}\circ I_f(x)-h(x)|= |I_g^{-1}\circ I_f(x)-I_g^{-1}\circ I_g\circ h(x)|\leq C |I_f(x)-I_g(h(x))|\\ &\quad=C\bigg|\!\int_0^xd\mu_f-\int_0^{h(x)}\,d\mu_g\bigg| \leq C\bigg|\!\int_0^xd\mu_f-\int_0^{h(x)}\,d\mu_g^N\bigg|\\ &\qquad+C\bigg|\!\int_0^{h(x)}\,d\mu_g^N-\int_0^{h(x)}\,d\mu_g\bigg|\\ &\quad=C\bigg|\!\int_0^xd\mu_f-\int_0^xd(h^*\mu_g^N)\bigg| +C\bigg|\!\int_0^{h(x)}\,d\mu_g^N-\int_0^{h(x)}\,d\mu_g\bigg|\\ &\quad=C\bigg|\!\int_0^x\,d\mu_f-\int_0^x\,d\mu_f^N\bigg| +C\bigg|\!\int_0^{h(x)}\,d\mu_g^N-\int_0^{h(x)}\,d\mu_g\bigg|,\end{align*} $$
$$ \begin{align*}&|{h}_N(x)-h(x)|\\&\quad=|I_g^{-1}\circ I_f(x)-h(x)|= |I_g^{-1}\circ I_f(x)-I_g^{-1}\circ I_g\circ h(x)|\leq C |I_f(x)-I_g(h(x))|\\ &\quad=C\bigg|\!\int_0^xd\mu_f-\int_0^{h(x)}\,d\mu_g\bigg| \leq C\bigg|\!\int_0^xd\mu_f-\int_0^{h(x)}\,d\mu_g^N\bigg|\\ &\qquad+C\bigg|\!\int_0^{h(x)}\,d\mu_g^N-\int_0^{h(x)}\,d\mu_g\bigg|\\ &\quad=C\bigg|\!\int_0^xd\mu_f-\int_0^xd(h^*\mu_g^N)\bigg| +C\bigg|\!\int_0^{h(x)}\,d\mu_g^N-\int_0^{h(x)}\,d\mu_g\bigg|\\ &\quad=C\bigg|\!\int_0^x\,d\mu_f-\int_0^x\,d\mu_f^N\bigg| +C\bigg|\!\int_0^{h(x)}\,d\mu_g^N-\int_0^{h(x)}\,d\mu_g\bigg|,\end{align*} $$
where
![]() $\sup |(I_g^{-1})'|=\sup |\rho _g^{-1}|\leq C$
. By symmetry, it suffices to show that
$\sup |(I_g^{-1})'|=\sup |\rho _g^{-1}|\leq C$
. By symmetry, it suffices to show that
 $$ \begin{align*} \bigg|\!\int_0^x\,d\mu_f-\int_0^x\,d\mu_f^N\bigg|\leq K\unicode{x3bb}^N, \end{align*} $$
$$ \begin{align*} \bigg|\!\int_0^x\,d\mu_f-\int_0^x\,d\mu_f^N\bigg|\leq K\unicode{x3bb}^N, \end{align*} $$
uniformly in
![]() $x\in S^1$
. This is precisely the content of Lemma 2.4. Therefore, we have shown that for every
$x\in S^1$
. This is precisely the content of Lemma 2.4. Therefore, we have shown that for every
![]() $x\in S^1$
,
$x\in S^1$
,
![]() $|{h}_N(x)-h(x)|\leq K\unicode{x3bb} ^{N}$
, where
$|{h}_N(x)-h(x)|\leq K\unicode{x3bb} ^{N}$
, where
![]() $\unicode{x3bb} =\tau ^{N/2}$
. This proves the first statement of Theorem 1.3.
$\unicode{x3bb} =\tau ^{N/2}$
. This proves the first statement of Theorem 1.3.
As a first consequence, we obtain a bound on the
![]() $C^0$
distance between f and
$C^0$
distance between f and
![]() $f_N$
:
$f_N$
:
 $$ \begin{align*} |f(x)-f_N(x)|&=|h^{-1}(g((h(x))-{h}_N^{-1}(g({h}_N(x))|\\&\leq |h^{-1}(g((h(x))-{h}_N^{-1}(g(h(x))|+ |{h}_N^{-1}(g((h(x))-{h}_N^{-1}(g({h}_N(x))|\\&\leq d_{C^0}(h^{-1},{h}_N^{-1})+Lip({h}_N^{-1}\circ g)d_{C^0}(h,{h}_N){\kern-1pt}\leq{\kern-1pt} K(1{\kern-1pt}+{\kern-1pt}Lip({h}_N^{-1}\circ g))\unicode{x3bb}^N. \end{align*} $$
$$ \begin{align*} |f(x)-f_N(x)|&=|h^{-1}(g((h(x))-{h}_N^{-1}(g({h}_N(x))|\\&\leq |h^{-1}(g((h(x))-{h}_N^{-1}(g(h(x))|+ |{h}_N^{-1}(g((h(x))-{h}_N^{-1}(g({h}_N(x))|\\&\leq d_{C^0}(h^{-1},{h}_N^{-1})+Lip({h}_N^{-1}\circ g)d_{C^0}(h,{h}_N){\kern-1pt}\leq{\kern-1pt} K(1{\kern-1pt}+{\kern-1pt}Lip({h}_N^{-1}\circ g))\unicode{x3bb}^N. \end{align*} $$
Note that
![]() $Lip({h}_N^{-1}\circ g)=\sup |D({h}_N^{-1}\circ g)|=\sup (|D(I_f^{-1}\circ I_g\circ g)|{\kern-1pt}\leq{\kern-1pt} ({\max \rho _g}/{\min \rho _f}) \max |g'|$
, which is uniformly bounded in
$Lip({h}_N^{-1}\circ g)=\sup |D({h}_N^{-1}\circ g)|=\sup (|D(I_f^{-1}\circ I_g\circ g)|{\kern-1pt}\leq{\kern-1pt} ({\max \rho _g}/{\min \rho _f}) \max |g'|$
, which is uniformly bounded in
![]() $\mathcal {W}$
. Absorbing these uniform constants into K, we get
$\mathcal {W}$
. Absorbing these uniform constants into K, we get
To finish the proof, it remains to establish the stated
![]() $C^1$
exponential closeness of f and
$C^1$
exponential closeness of f and
![]() $f_N$
. We will do so by interpolating between the
$f_N$
. We will do so by interpolating between the
![]() $C^0$
exponential bound in equation (2.5) and a uniform
$C^0$
exponential bound in equation (2.5) and a uniform
![]() $C^{1+\alpha }$
bound we will establish below. The following interpolation lemma we will use is elementary, but we include the proof for completeness.
$C^{1+\alpha }$
bound we will establish below. The following interpolation lemma we will use is elementary, but we include the proof for completeness.
Lemma 2.5. Fix
![]() $M>0$
and
$M>0$
and
![]() $0<\alpha \leq 1$
. Let
$0<\alpha \leq 1$
. Let
![]() $\phi :S^1\rightarrow S^1$
be a
$\phi :S^1\rightarrow S^1$
be a
![]() $C^{1+\alpha }$
function with
$C^{1+\alpha }$
function with
![]() $|\phi '|_{C^\alpha }$
$|\phi '|_{C^\alpha }$
![]() $<M$
, and let
$<M$
, and let
![]() $\varepsilon ,\delta>0$
be such that
$\varepsilon ,\delta>0$
be such that
 $$ \begin{align*}\sup_{|x-y|>\delta}\frac{|\phi(x)-\phi(y)|}{|x-y|}<\varepsilon,\end{align*} $$
$$ \begin{align*}\sup_{|x-y|>\delta}\frac{|\phi(x)-\phi(y)|}{|x-y|}<\varepsilon,\end{align*} $$
then
![]() $|\phi |_{C^1}<({M}/({\alpha +1}))\delta ^\alpha +\varepsilon $
.
$|\phi |_{C^1}<({M}/({\alpha +1}))\delta ^\alpha +\varepsilon $
.
Proof of Lemma 2.5
Suppose first that
![]() $\phi (0)=0$
and
$\phi (0)=0$
and
![]() $\phi '(0)=\sup |\phi '|=:\varepsilon '$
, and take
$\phi '(0)=\sup |\phi '|=:\varepsilon '$
, and take
![]() $|x|>\delta $
. Then, since the
$|x|>\delta $
. Then, since the
![]() $\alpha $
-Hölder seminorm of
$\alpha $
-Hölder seminorm of
![]() $\phi '$
is bounded by M, we have
$\phi '$
is bounded by M, we have
 $$ \begin{align*} \max_{y\neq 0}\frac{|\phi'(0)-\phi'(y)|}{|y|^\alpha}&<M\implies -M|y|^\alpha\leq \phi'(0)-\phi'(y)\\&\leq M|y|^\alpha\implies \phi'(y)\geq \phi'(0)-M|y|^\alpha. \end{align*} $$
$$ \begin{align*} \max_{y\neq 0}\frac{|\phi'(0)-\phi'(y)|}{|y|^\alpha}&<M\implies -M|y|^\alpha\leq \phi'(0)-\phi'(y)\\&\leq M|y|^\alpha\implies \phi'(y)\geq \phi'(0)-M|y|^\alpha. \end{align*} $$
Putting this together with
we find
It follows that
where in the last line, we let
![]() $|x|\rightarrow \delta $
. Finally, if
$|x|\rightarrow \delta $
. Finally, if
![]() $|\phi |_{C^0}$
is attained at some other point
$|\phi |_{C^0}$
is attained at some other point
![]() $x_0\in S^1$
, then simply apply the preceding argument to
$x_0\in S^1$
, then simply apply the preceding argument to
![]() $\tilde {\phi }(x)=\phi (x+x_0)-\phi (0)$
.
$\tilde {\phi }(x)=\phi (x+x_0)-\phi (0)$
.
We now return to finish the proof of Theorem 1.3. We will apply Lemma 2.5 to the function
![]() $F={f}_N-f$
. Let
$F={f}_N-f$
. Let
![]() $\varepsilon =2K'\unicode{x3bb} ^{N/2}$
and
$\varepsilon =2K'\unicode{x3bb} ^{N/2}$
and
![]() $\delta =\unicode{x3bb} ^{N/2}$
. Then,
$\delta =\unicode{x3bb} ^{N/2}$
. Then,
 $$ \begin{align*} \sup_{|x-y|>\delta}\frac{|F(x)-F(y)|}{|x-y|}<\frac{2|F|_{C^0}}{\delta}\leq \frac{2K'd_{C^0}(h,{h}_N)}{\unicode{x3bb}^{N/2}}\leq \frac{2K'\unicode{x3bb}^N}{\unicode{x3bb}^{N/2}}=2K'\unicode{x3bb}^{N/2}. \end{align*} $$
$$ \begin{align*} \sup_{|x-y|>\delta}\frac{|F(x)-F(y)|}{|x-y|}<\frac{2|F|_{C^0}}{\delta}\leq \frac{2K'd_{C^0}(h,{h}_N)}{\unicode{x3bb}^{N/2}}\leq \frac{2K'\unicode{x3bb}^N}{\unicode{x3bb}^{N/2}}=2K'\unicode{x3bb}^{N/2}. \end{align*} $$
It remains to prove that
![]() $|F'|_{C^\alpha }$
is uniformly bounded for
$|F'|_{C^\alpha }$
is uniformly bounded for
![]() $f\in \mathcal {W}$
for every
$f\in \mathcal {W}$
for every
![]() $\alpha <1$
. We have
$\alpha <1$
. We have
and since f is uniformly bounded in the
![]() $C^2$
seminorm, it will be uniformly bounded in the
$C^2$
seminorm, it will be uniformly bounded in the
![]() $C^{1+\alpha }$
seminorm. So it remains to uniformly bound
$C^{1+\alpha }$
seminorm. So it remains to uniformly bound
![]() $|{f}_N'|_{C^\alpha }=|(h_N^{-1}\circ g\circ h_N)'|_{C^\alpha }=|((h_N^{-1})'\circ g\circ h_N)(g'\circ h_N)h_N'|_{C^\alpha }$
. By the product rule for the
$|{f}_N'|_{C^\alpha }=|(h_N^{-1}\circ g\circ h_N)'|_{C^\alpha }=|((h_N^{-1})'\circ g\circ h_N)(g'\circ h_N)h_N'|_{C^\alpha }$
. By the product rule for the
![]() $\alpha -$
Hölder seminorm and symmetry between
$\alpha -$
Hölder seminorm and symmetry between
![]() $h_N=I_g^{-1}\circ I_f$
and
$h_N=I_g^{-1}\circ I_f$
and
![]() $h_N^{-1}=I_f^{-1}\circ I_g$
, it suffices to uniformly bound
$h_N^{-1}=I_f^{-1}\circ I_g$
, it suffices to uniformly bound
![]() $|h_N'|_{C^\alpha }=|{\rho _f}/({\rho _g\circ h_N})|_{C^\alpha }$
. By Lemma 2.1, we can uniformly bound
$|h_N'|_{C^\alpha }=|{\rho _f}/({\rho _g\circ h_N})|_{C^\alpha }$
. By Lemma 2.1, we can uniformly bound
![]() $|\rho _f|_{C^\alpha }$
for
$|\rho _f|_{C^\alpha }$
for
![]() $f\in \mathcal {W}$
and hence, by properties of the
$f\in \mathcal {W}$
and hence, by properties of the
![]() $\alpha -$
Hölder seminorm, we can uniformly bound
$\alpha -$
Hölder seminorm, we can uniformly bound
![]() $|{\rho _f}/({\rho _g\circ h_N})|_{C^\alpha }.$
Therefore, we may apply Lemma 2.5 and we find that
$|{\rho _f}/({\rho _g\circ h_N})|_{C^\alpha }.$
Therefore, we may apply Lemma 2.5 and we find that
![]() $|F|_{C^1}\leq ({M}/({\alpha +1}))\delta ^\alpha +\varepsilon = ({M}/({\alpha +1}))(2K'\unicode{x3bb} ^{\alpha N/2})+\unicode{x3bb} ^{N/2}=K"\unicode{x3bb} ^{\alpha N/2}$
. For
$|F|_{C^1}\leq ({M}/({\alpha +1}))\delta ^\alpha +\varepsilon = ({M}/({\alpha +1}))(2K'\unicode{x3bb} ^{\alpha N/2})+\unicode{x3bb} ^{N/2}=K"\unicode{x3bb} ^{\alpha N/2}$
. For
![]() $\alpha <1$
such that
$\alpha <1$
such that
![]() $\unicode{x3bb} ^{\alpha /2}=\unicode{x3bb} _0$
, we get the desired conclusion.
$\unicode{x3bb} ^{\alpha /2}=\unicode{x3bb} _0$
, we get the desired conclusion.
Corollary 2.6. Let
![]() $f,g\in \operatorname {\mathrm {Exp}}^{r+1+\alpha }_\gamma (S^1)$
for
$f,g\in \operatorname {\mathrm {Exp}}^{r+1+\alpha }_\gamma (S^1)$
for
![]() $r\in \mathbb {N}$
,
$r\in \mathbb {N}$
,
![]() $r\geq 2$
, and suppose that
$r\geq 2$
, and suppose that
![]() $d_{C^{r+1+\alpha }}(f,g)<C_0$
. Under the same hypotheses of Theorem 1.3, we have that there exists a constant
$d_{C^{r+1+\alpha }}(f,g)<C_0$
. Under the same hypotheses of Theorem 1.3, we have that there exists a constant
![]() $K_r>0$
independent of f such that
$K_r>0$
independent of f such that
![]() $d_{C^r}(f,{f}_N)\leq K_r\unicode{x3bb} ^{2^{-r}N}$
.
$d_{C^r}(f,{f}_N)\leq K_r\unicode{x3bb} ^{2^{-r}N}$
.
Proof. We proceed by induction. The base case
![]() $r=2$
follows exactly as in Theorem 1.3, except the added assumption that our systems are
$r=2$
follows exactly as in Theorem 1.3, except the added assumption that our systems are
![]() $C^{2+\alpha }$
allow us to get uniform bounds on
$C^{2+\alpha }$
allow us to get uniform bounds on
![]() $|F'|_{C^1}$
(using the argument of Lemma 2.1) and apply Lemma 2.5 with
$|F'|_{C^1}$
(using the argument of Lemma 2.1) and apply Lemma 2.5 with
![]() $\alpha =1$
. Letting
$\alpha =1$
. Letting
![]() $F={f}_N-f$
, we assume by induction that we have proven
$F={f}_N-f$
, we assume by induction that we have proven
![]() $|F|_{C^r}\leq K_r\unicode{x3bb} ^{2^{-r}N}$
. To obtain a similar estimate for
$|F|_{C^r}\leq K_r\unicode{x3bb} ^{2^{-r}N}$
. To obtain a similar estimate for
![]() $|F|_{C^{r+1}}$
, we apply Lemma 2.5 to the function
$|F|_{C^{r+1}}$
, we apply Lemma 2.5 to the function
![]() $F^{(r)}$
, with
$F^{(r)}$
, with
![]() $\varepsilon =2K_r\unicode{x3bb} ^{2^{-r-1}N}$
and
$\varepsilon =2K_r\unicode{x3bb} ^{2^{-r-1}N}$
and
![]() $\delta =\unicode{x3bb} ^{2^{-r-1}N}.$
For these choices, we find
$\delta =\unicode{x3bb} ^{2^{-r-1}N}.$
For these choices, we find
 $$ \begin{align*} \sup_{|x-y|>\delta}\frac{|F^{(r)}(x)-F^{(r)}(y)|}{|x-y|}<\frac{2|F|_{C^r}}{\unicode{x3bb}^{2^{-r}N}}\leq \frac{2K_{r}\unicode{x3bb}^{2^{-r}N}}{\unicode{x3bb}^{2^{-r-1}N}}=K_r\unicode{x3bb}^{2^{-r-1}N}. \end{align*} $$
$$ \begin{align*} \sup_{|x-y|>\delta}\frac{|F^{(r)}(x)-F^{(r)}(y)|}{|x-y|}<\frac{2|F|_{C^r}}{\unicode{x3bb}^{2^{-r}N}}\leq \frac{2K_{r}\unicode{x3bb}^{2^{-r}N}}{\unicode{x3bb}^{2^{-r-1}N}}=K_r\unicode{x3bb}^{2^{-r-1}N}. \end{align*} $$
The assumption that maps are
![]() $C^{r+2+\alpha }$
is so that we can compactly embed the set
$C^{r+2+\alpha }$
is so that we can compactly embed the set
![]() $\mathcal {W}$
in
$\mathcal {W}$
in
![]() $C^{r+2}$
, thereby getting uniform bounds on
$C^{r+2}$
, thereby getting uniform bounds on
![]() $|F^{(r+1)}|_{C^1}$
. The conclusion now follows Lemma 2.5 exactly as in the proof of Theorem 1.3.
$|F^{(r+1)}|_{C^1}$
. The conclusion now follows Lemma 2.5 exactly as in the proof of Theorem 1.3.
The next corollary establishes a similar estimate on the exponential decay of
![]() $d_{C^r}(f,{f}_N)$
without such a loss of exponent under the stronger assumption that f and g are close in the
$d_{C^r}(f,{f}_N)$
without such a loss of exponent under the stronger assumption that f and g are close in the
![]() $C^k$
-topology for all k.
$C^k$
-topology for all k.
Corollary 2.7. Let
![]() $f,g\in \operatorname {\mathrm {Exp}}^{\infty }_\gamma (S^1)$
and suppose that
$f,g\in \operatorname {\mathrm {Exp}}^{\infty }_\gamma (S^1)$
and suppose that
![]() $\sup _{k\geq 0}d_{C^k}(f,g)<C_0$
. Then, for any
$\sup _{k\geq 0}d_{C^k}(f,g)<C_0$
. Then, for any
![]() $r\in \mathbb {N}$
and any
$r\in \mathbb {N}$
and any
![]() $0<\unicode{x3bb} ^{1/2}<\unicode{x3bb} _0<1$
, there exists a constant
$0<\unicode{x3bb} ^{1/2}<\unicode{x3bb} _0<1$
, there exists a constant
![]() $K_r'>0$
such that under the hypotheses of Theorem 1.3, we have
$K_r'>0$
such that under the hypotheses of Theorem 1.3, we have
![]() $d_{C^r}(f,{f}_N)\leq K_r'\unicode{x3bb} _0^N$
.
$d_{C^r}(f,{f}_N)\leq K_r'\unicode{x3bb} _0^N$
.
Proof. The proof follows from interpolation theory on the spaces
![]() $C^r(S^1)$
(see Lunardi [Reference LunardiLun18, Remark 1.22]). For
$C^r(S^1)$
(see Lunardi [Reference LunardiLun18, Remark 1.22]). For
![]() $k_1<m<k_2\in \mathbb {N}$
, we have that
$k_1<m<k_2\in \mathbb {N}$
, we have that
![]() $\|\phi \|_{C^m}\leq C_{k_1,k_2,m}\|\phi \|_{C^{k_1}}^{1-t}\|\phi \|_{C^{k_2}}^t$
for any
$\|\phi \|_{C^m}\leq C_{k_1,k_2,m}\|\phi \|_{C^{k_1}}^{1-t}\|\phi \|_{C^{k_2}}^t$
for any
![]() $\phi \in C^{k_2}(S^1)$
, where
$\phi \in C^{k_2}(S^1)$
, where
![]() $t=({m-k_1})/({k_2-k_1})$
. We will apply this with
$t=({m-k_1})/({k_2-k_1})$
. We will apply this with
![]() $\phi =F={f}_N-f, k_1=1$
, and by taking
$\phi =F={f}_N-f, k_1=1$
, and by taking
![]() $k_2$
sufficiently large, we have that t can be made arbitrarily close to
$k_2$
sufficiently large, we have that t can be made arbitrarily close to
![]() $0$
. We choose
$0$
. We choose
![]() $k_2$
so that
$k_2$
so that
![]() $\unicode{x3bb} ^{({1-t})/{2}}\leq \unicode{x3bb} _0$
. We want to bound the term
$\unicode{x3bb} ^{({1-t})/{2}}\leq \unicode{x3bb} _0$
. We want to bound the term
![]() $\|F\|_{C^{k_2}}$
using the bound
$\|F\|_{C^{k_2}}$
using the bound
![]() $d_{C^{k_2+2}}(f,g)<C_0$
. Applying Corollary 2.1 gives us
$d_{C^{k_2+2}}(f,g)<C_0$
. Applying Corollary 2.1 gives us
![]() $\|F\|_{C^{k_2}}\leq K_{k_2}\unicode{x3bb} ^{{tN}/{2^{k_2}}}\leq K_{k_2}$
. Hence, by our interpolation inequality (collecting all constants into C),
$\|F\|_{C^{k_2}}\leq K_{k_2}\unicode{x3bb} ^{{tN}/{2^{k_2}}}\leq K_{k_2}$
. Hence, by our interpolation inequality (collecting all constants into C),
3. Effective equidistribution
We begin by reviewing the basic definitions of subshifts of finite type and transfer operators. For a more detailed treatment, see Baladi [Reference BaladiBal00], and Parry and Pollicott [Reference Parry and PollicottPP90]. Let A be an irreducible and aperiodic
![]() $0,1$
-matrix, which we will refer to as a transition matrix, and consider the set
$0,1$
-matrix, which we will refer to as a transition matrix, and consider the set
We interpret
![]() $\Sigma _A^+$
as the set of all sequences in m-symbols that are allowed by the transition matrix A. Consider the left shift map
$\Sigma _A^+$
as the set of all sequences in m-symbols that are allowed by the transition matrix A. Consider the left shift map
![]() $\sigma _A^+:\Sigma _A^+\rightarrow \Sigma _A^+$
defined by
$\sigma _A^+:\Sigma _A^+\rightarrow \Sigma _A^+$
defined by
![]() $(\sigma _A^+(x))_n=x_{n+1}$
. We refer to the dynamical system
$(\sigma _A^+(x))_n=x_{n+1}$
. We refer to the dynamical system
![]() $(\Sigma _A^+,\sigma _A^+)$
as a one-sided subshift of finite type. We can analogously define two-sided subshifts of finite types. When our transition matrix is clear, we shall denote the left shift map simply as
$(\Sigma _A^+,\sigma _A^+)$
as a one-sided subshift of finite type. We can analogously define two-sided subshifts of finite types. When our transition matrix is clear, we shall denote the left shift map simply as
![]() $\sigma $
.
$\sigma $
.
We topologize
![]() $\Sigma _A^+$
with the metric
$\Sigma _A^+$
with the metric
![]() $d_{\theta }(x,y)=\theta ^{\max \{n\geq 0|x_i=y_i, 0\leq i<n\}}$
, where
$d_{\theta }(x,y)=\theta ^{\max \{n\geq 0|x_i=y_i, 0\leq i<n\}}$
, where
![]() $0<\theta <1$
is a fixed constant. Notice that with respect to this metric,
$0<\theta <1$
is a fixed constant. Notice that with respect to this metric,
![]() $\sigma $
is a
$\sigma $
is a
![]() $\theta $
-expansion. Let
$\theta $
-expansion. Let
![]() $\mathcal {F}_\theta ^+$
denote the Banach space of all functions
$\mathcal {F}_\theta ^+$
denote the Banach space of all functions
![]() $\phi :\Sigma _A^+\rightarrow \mathbb {C}$
which are Lipschitz continuous with respect to this metric. Denote by
$\phi :\Sigma _A^+\rightarrow \mathbb {C}$
which are Lipschitz continuous with respect to this metric. Denote by
![]() $|\cdot |_\theta $
and
$|\cdot |_\theta $
and
![]() $\|\cdot \|_\theta $
the Lipschitz seminorm and Lipschitz norm with respect to this metric, respectively. For
$\|\cdot \|_\theta $
the Lipschitz seminorm and Lipschitz norm with respect to this metric, respectively. For
![]() $1\leq i\leq m,$
let
$1\leq i\leq m,$
let
![]() $[i]=\{x\in \Sigma _A^+|x_0=i\}$
, which we call the cylinder set at i. We will use the following important but simple estimate.
$[i]=\{x\in \Sigma _A^+|x_0=i\}$
, which we call the cylinder set at i. We will use the following important but simple estimate.
Lemma 3.1. If
![]() $\phi \in \mathcal {F}_\theta $
and
$\phi \in \mathcal {F}_\theta $
and
![]() $[i]$
is a cylinder set, then
$[i]$
is a cylinder set, then
![]() $\|\chi _{[i]}\phi \|_\theta <2\|\phi \|_\theta $
.
$\|\chi _{[i]}\phi \|_\theta <2\|\phi \|_\theta $
.
Proof. Note that we always have
![]() $\|\chi _{[i]}\phi \|_{\infty }\leq \|\phi \|_\infty \leq \|\phi \|_\theta $
, so it remains to prove that
$\|\chi _{[i]}\phi \|_{\infty }\leq \|\phi \|_\infty \leq \|\phi \|_\theta $
, so it remains to prove that
![]() $|\chi _{[i]}\phi |_\theta \leq \|\phi \|_\theta $
. Suppose that
$|\chi _{[i]}\phi |_\theta \leq \|\phi \|_\theta $
. Suppose that
![]() $x\neq y$
. If
$x\neq y$
. If
![]() $x,y\in [i]$
, we have
$x,y\in [i]$
, we have
If
![]() $x\not \in [i]$
and
$x\not \in [i]$
and
![]() $y\not \in [i]$
, then
$y\not \in [i]$
, then
Finally, if
![]() $x\in [i]$
and
$x\in [i]$
and
![]() $y\not \in [i]$
, then since
$y\not \in [i]$
, then since
![]() $d_\theta (x,y)=1$
, we have
$d_\theta (x,y)=1$
, we have
Taking the supremum over
![]() $x\neq y$
yields
$x\neq y$
yields
![]() $|\chi _{[i]}\phi |_\theta \leq \|\phi \|_\theta ,$
as desired.
$|\chi _{[i]}\phi |_\theta \leq \|\phi \|_\theta ,$
as desired.
Our primary tool in this section will be the Ruelle transfer operator.
Definition 3.1. Fix a weight function
![]() $\psi \in \mathcal {F}_\theta ^+$
and define the Ruelle transfer operator
$\psi \in \mathcal {F}_\theta ^+$
and define the Ruelle transfer operator
![]() $\mathcal {L}_\psi :\mathcal {F}_\theta ^+\rightarrow \mathcal {F}_\theta ^+$
by the formula
$\mathcal {L}_\psi :\mathcal {F}_\theta ^+\rightarrow \mathcal {F}_\theta ^+$
by the formula
 $$ \begin{align*} \mathcal{L}_\psi(\phi)(x)=\sum_{\sigma(y)=x}e^{\psi(y)}\phi(y). \end{align*} $$
$$ \begin{align*} \mathcal{L}_\psi(\phi)(x)=\sum_{\sigma(y)=x}e^{\psi(y)}\phi(y). \end{align*} $$
By the Ruelle–Perron–Frobenius theorem (see [Reference BaladiBal00, Theorem 1.5]), the operator
![]() $\mathcal {L}_\psi $
is quasi-compact, with a unique maximal positive simple eigenvalue
$\mathcal {L}_\psi $
is quasi-compact, with a unique maximal positive simple eigenvalue
![]() $\unicode{x3bb} =e^{P(\psi )}$
corresponding to a strictly positive eigenfunction
$\unicode{x3bb} =e^{P(\psi )}$
corresponding to a strictly positive eigenfunction
![]() $\rho $
, and all other points of the spectrum lie in a strictly smaller disc. Let us further assume that the transfer operator is normalized so that
$\rho $
, and all other points of the spectrum lie in a strictly smaller disc. Let us further assume that the transfer operator is normalized so that
![]() $\mathcal {L}_\psi (1)=e^{P(\psi )}$
(which can always be accomplished by replacing the weight
$\mathcal {L}_\psi (1)=e^{P(\psi )}$
(which can always be accomplished by replacing the weight
![]() $\psi $
with
$\psi $
with
![]() $\overline {\psi }=\psi +\log (\rho )-\log (\rho )\circ \sigma $
, and observing that
$\overline {\psi }=\psi +\log (\rho )-\log (\rho )\circ \sigma $
, and observing that
![]() $P(\psi )=P(\overline {\psi }))$
. Then the eigenmeasure
$P(\psi )=P(\overline {\psi }))$
. Then the eigenmeasure
![]() $\mu _\psi $
corresponding to the eigenvalue
$\mu _\psi $
corresponding to the eigenvalue
![]() $e^{P(\psi )}$
of the dual operator
$e^{P(\psi )}$
of the dual operator
![]() $\mathcal {L}_\psi ^*$
is the unique equilibrium state of the potential
$\mathcal {L}_\psi ^*$
is the unique equilibrium state of the potential
![]() $\psi $
. Observe that
$\psi $
. Observe that
 $$ \begin{align*} \mathcal{L}_\psi^n(\phi)(x)=\sum_{\sigma^n(y)=x}e^{S_n\psi(y)}\phi(y). \end{align*} $$
$$ \begin{align*} \mathcal{L}_\psi^n(\phi)(x)=\sum_{\sigma^n(y)=x}e^{S_n\psi(y)}\phi(y). \end{align*} $$
What follows is the analog of Theorem 3.2 for subshifts of finite type.
Theorem 3.2. (Effective equidistribution for equilibrium states)
Let
![]() $(\Sigma _A^+,\sigma _A^+)$
be a subshift of finite type, where the
$(\Sigma _A^+,\sigma _A^+)$
be a subshift of finite type, where the
![]() $m\times m$
transition matrix A is irreducible and aperiodic, and let
$m\times m$
transition matrix A is irreducible and aperiodic, and let
![]() $\psi \in \mathcal {F}_\theta ^+$
be a Lipschitz continuous potential. Then, there exists constants
$\psi \in \mathcal {F}_\theta ^+$
be a Lipschitz continuous potential. Then, there exists constants
![]() $C>0$
and
$C>0$
and
![]() $0<\tau <1$
such that for any
$0<\tau <1$
such that for any
![]() $\phi \in \mathcal {F}_\theta ^+$
and all
$\phi \in \mathcal {F}_\theta ^+$
and all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $$ \begin{align*} \bigg|\!\int \phi \,d\mu^n_\psi-\int \phi \,d\mu_\psi\bigg|\leq C\|\phi\|_\theta\tau^n, \end{align*} $$
$$ \begin{align*} \bigg|\!\int \phi \,d\mu^n_\psi-\int \phi \,d\mu_\psi\bigg|\leq C\|\phi\|_\theta\tau^n, \end{align*} $$
where
![]() $\mu _\psi $
is the unique equilibrium state of
$\mu _\psi $
is the unique equilibrium state of
![]() $\psi $
.
$\psi $
.
Remark 4. To be consistent with our previous notation in §2, we should write
![]() $\mu ^n_{\sigma ,\psi }$
for the weighted discrete measure. However, since the dynamics on the shift space will always be the left shift map
$\mu ^n_{\sigma ,\psi }$
for the weighted discrete measure. However, since the dynamics on the shift space will always be the left shift map
![]() $\sigma $
, we do not need to specify in our notation and will instead simply write
$\sigma $
, we do not need to specify in our notation and will instead simply write
![]() $\mu ^n_\psi $
.
$\mu ^n_\psi $
.
Proof. By replacing
![]() $\phi $
by
$\phi $
by
![]() $\phi -\int \phi \,d\mu _\psi $
, we may assume that
$\phi -\int \phi \,d\mu _\psi $
, we may assume that
![]() $\int \phi \,d\mu _\psi =0$
. We need to show that
$\int \phi \,d\mu _\psi =0$
. We need to show that
 $$ \begin{align} \bigg|\frac{1}{Z_n}\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)\bigg|\leq C\|\phi\|_\theta\tau^n, \end{align} $$
$$ \begin{align} \bigg|\frac{1}{Z_n}\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)\bigg|\leq C\|\phi\|_\theta\tau^n, \end{align} $$
where
![]() $Z_n$
is the normalization constant. By Katok and Hasselblatt [Reference Katok and HasselblattKH95, Proposition 20.3.3], there exists a constant
$Z_n$
is the normalization constant. By Katok and Hasselblatt [Reference Katok and HasselblattKH95, Proposition 20.3.3], there exists a constant
![]() $D>0$
such that
$D>0$
such that
![]() $({1}/{D})e^{nP(\psi )}\leq Z_n\leq De^{nP(\psi )}$
(an inspection of the proof reveals that this constant D can be made uniform). Let
$({1}/{D})e^{nP(\psi )}\leq Z_n\leq De^{nP(\psi )}$
(an inspection of the proof reveals that this constant D can be made uniform). Let
![]() $[i]=\{x\in \Sigma _A^+|x_0=i\}$
, and for a string
$[i]=\{x\in \Sigma _A^+|x_0=i\}$
, and for a string
![]() $\underline {i}=(i_0,\ldots ,i_{n-1})$
, let us denote its length by
$\underline {i}=(i_0,\ldots ,i_{n-1})$
, let us denote its length by
![]() $|\underline {i}|=n$
and its cylinder set by
$|\underline {i}|=n$
and its cylinder set by
![]() $[\underline {i}]=\{x\in \Sigma _A^+|x_0=i_0,\ldots ,x_{n-1}\}$
. For each
$[\underline {i}]=\{x\in \Sigma _A^+|x_0=i_0,\ldots ,x_{n-1}\}$
. For each
![]() $1\leq i\leq m$
, fix any point
$1\leq i\leq m$
, fix any point
![]() $x_i\in [i]$
, and for each string
$x_i\in [i]$
, and for each string
![]() $\underline {i}$
, fix a point of period n,
$\underline {i}$
, fix a point of period n,
![]() $x_{\underline {i}}\in [\underline {i}]$
, if one exists, and let
$x_{\underline {i}}\in [\underline {i}]$
, if one exists, and let
![]() $x_{\underline {i}}\in [\underline {i}]$
be arbitrary otherwise. We first claim that
$x_{\underline {i}}\in [\underline {i}]$
be arbitrary otherwise. We first claim that
 $$ \begin{align*} \sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)=\sum_{|\underline{i}|=n}\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}}). \end{align*} $$
$$ \begin{align*} \sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)=\sum_{|\underline{i}|=n}\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}}). \end{align*} $$
To see this, we expand out each term in the right sum:
 $$ \begin{align*} \mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})=\sum_{\sigma^n(y)=x_{\underline{i}}}e^{S_n\psi(y)}\chi_{[\underline{i}]}(y)\phi(y) =e^{S_n\psi(\underline{i}x_{\underline{i}})}\phi(\underline{i}x_{\underline{i}})=e^{S_n\psi(x_{\underline{i}})}\phi(x_{\underline{i}}), \end{align*} $$
$$ \begin{align*} \mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})=\sum_{\sigma^n(y)=x_{\underline{i}}}e^{S_n\psi(y)}\chi_{[\underline{i}]}(y)\phi(y) =e^{S_n\psi(\underline{i}x_{\underline{i}})}\phi(\underline{i}x_{\underline{i}})=e^{S_n\psi(x_{\underline{i}})}\phi(x_{\underline{i}}), \end{align*} $$
where
![]() $\underline {i}x=(i_0,\ldots ,i_{n-1},x_0,x_1,\ldots )$
denotes the only inverse branch of
$\underline {i}x=(i_0,\ldots ,i_{n-1},x_0,x_1,\ldots )$
denotes the only inverse branch of
![]() $\sigma ^n$
that contributes to the sum due to the characteristic function. Since each point of
$\sigma ^n$
that contributes to the sum due to the characteristic function. Since each point of
![]() $\operatorname {\mathrm {Fix}}(\sigma ^n)$
lies in a unique cylinder set
$\operatorname {\mathrm {Fix}}(\sigma ^n)$
lies in a unique cylinder set
![]() $[\underline {i}]$
, and each such cylinder set contains at most one period-n point, we see that all periodic points are accounted for in the sum over
$[\underline {i}]$
, and each such cylinder set contains at most one period-n point, we see that all periodic points are accounted for in the sum over
![]() $|\underline {i}|=n$
. Consider the estimate
$|\underline {i}|=n$
. Consider the estimate
 $$ \begin{align} \bigg|\!\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)\bigg|&\leq\bigg|\!\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)-\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg|\nonumber\\&\quad+\bigg|\!\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg|. \end{align} $$
$$ \begin{align} \bigg|\!\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)\bigg|&\leq\bigg|\!\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)-\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg|\nonumber\\&\quad+\bigg|\!\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg|. \end{align} $$
To estimate both terms on the right, we will first decompose the transfer operator as a sum of its projection onto the eigenspace of
![]() $e^{P(\psi )}$
, and the orthogonal projection:
$e^{P(\psi )}$
, and the orthogonal projection:
![]() $\mathcal {L}_\psi =\mathcal {P}+\mathcal {N}$
, where
$\mathcal {L}_\psi =\mathcal {P}+\mathcal {N}$
, where
![]() $\mathcal {P}(\phi )=e^{P(\psi )}\int \phi \,d\mu _\psi $
, and
$\mathcal {P}(\phi )=e^{P(\psi )}\int \phi \,d\mu _\psi $
, and
![]() $\mathcal {N}$
has spectral radius
$\mathcal {N}$
has spectral radius
![]() $re^{P(\psi )}$
with
$re^{P(\psi )}$
with
![]() $0<r<1$
. The second term can thus be estimated as
$0<r<1$
. The second term can thus be estimated as
 $$ \begin{align} \bigg|\!\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg|&\leq \bigg|\!\sum_{k=1}^m\bigg[\mathcal{P}^n(\chi_{[i]}\phi)(x_i)+\mathcal{N}^n(\chi_{[i]}\phi)(x_i)\bigg]\bigg|\nonumber\\ &=\bigg|\!\sum_{k=1}^m\bigg[e^{nP(\psi)}\int_{[i]}\phi \,d\mu_\psi+\mathcal{N}^n(\chi_{[i]}\phi)(x_i)\bigg]\bigg|\nonumber\\ &=\bigg|e^{nP(\psi)}\int\phi \,d\mu_\psi+\sum_{k=1}^m\mathcal{N}^n(\chi_{[i]}\phi)(x_i)\bigg|=\bigg|\!\sum_{k=1}^m\mathcal{N}^n(\chi_{[i]}\phi)(x_i)\bigg|\nonumber\\&\leq \sum_{k=1}^m\|\mathcal{N}^n\|\|\chi_{[i]}\phi\|_\theta\leq C(r+\varepsilon)^ne^{nP(\psi)}\|\phi\|_\theta, \end{align} $$
$$ \begin{align} \bigg|\!\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg|&\leq \bigg|\!\sum_{k=1}^m\bigg[\mathcal{P}^n(\chi_{[i]}\phi)(x_i)+\mathcal{N}^n(\chi_{[i]}\phi)(x_i)\bigg]\bigg|\nonumber\\ &=\bigg|\!\sum_{k=1}^m\bigg[e^{nP(\psi)}\int_{[i]}\phi \,d\mu_\psi+\mathcal{N}^n(\chi_{[i]}\phi)(x_i)\bigg]\bigg|\nonumber\\ &=\bigg|e^{nP(\psi)}\int\phi \,d\mu_\psi+\sum_{k=1}^m\mathcal{N}^n(\chi_{[i]}\phi)(x_i)\bigg|=\bigg|\!\sum_{k=1}^m\mathcal{N}^n(\chi_{[i]}\phi)(x_i)\bigg|\nonumber\\&\leq \sum_{k=1}^m\|\mathcal{N}^n\|\|\chi_{[i]}\phi\|_\theta\leq C(r+\varepsilon)^ne^{nP(\psi)}\|\phi\|_\theta, \end{align} $$
using Lemma 3.1 and the spectral radius formula (see also Lemma 3.3 for the uniform version we will need later in the case of the symbolic coding of expanding maps), where
![]() $\varepsilon>0$
is arbitrary and
$\varepsilon>0$
is arbitrary and
![]() $C>0$
depends on
$C>0$
depends on
![]() $\varepsilon $
(recall that m is the size of our alphabet and is independent of n).
$\varepsilon $
(recall that m is the size of our alphabet and is independent of n).
It remains to estimate
 $$ \begin{align*} \bigg|\!\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)-\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg| =\bigg|\!\sum_{|\underline{i}|=n}\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg|. \end{align*} $$
$$ \begin{align*} \bigg|\!\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)-\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg| =\bigg|\!\sum_{|\underline{i}|=n}\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg|. \end{align*} $$
If
![]() $\underline {i}=(i_0,\ldots ,i_{n-1})$
, we let
$\underline {i}=(i_0,\ldots ,i_{n-1})$
, we let
![]() $\underline {j}(\underline {i})=(i_0,\ldots ,i_{n-2})$
. We now telescope our above series:
$\underline {j}(\underline {i})=(i_0,\ldots ,i_{n-2})$
. We now telescope our above series:
 $$ \begin{align*} &\sum_{|\underline{i}|=n}\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\\&\quad=\sum_{m=2}^n\bigg(\sum_{|\underline{i}|=m}\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}}) -\sum_{|\underline{i}|=m-1}\mathcal{L}_\psi^n(\chi_{[\underline{j}]}\phi)(x_{\underline{j}})\bigg)\\&\quad=\sum_{m=2}^n\sum_{|\underline{i}|=m}(\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{j}(\underline{i})}))\\&\quad=\sum_{m=2}^n\sum_{|\underline{i}|=m}((\mathcal{P}^n+\mathcal{N}^n)(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-(\mathcal{P}^n+\mathcal{N}^n)(\chi_{[\underline{i}]}\phi)(x_{\underline{j}(\underline{i})}))\\&\quad=\sum_{m=2}^n\sum_{|\underline{i}|=m}(\mathcal{N}^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\mathcal{N}^n(\chi_{[\underline{i}]}\phi)(x_{\underline{j}(\underline{i})})). \end{align*} $$
$$ \begin{align*} &\sum_{|\underline{i}|=n}\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\\&\quad=\sum_{m=2}^n\bigg(\sum_{|\underline{i}|=m}\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}}) -\sum_{|\underline{i}|=m-1}\mathcal{L}_\psi^n(\chi_{[\underline{j}]}\phi)(x_{\underline{j}})\bigg)\\&\quad=\sum_{m=2}^n\sum_{|\underline{i}|=m}(\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{j}(\underline{i})}))\\&\quad=\sum_{m=2}^n\sum_{|\underline{i}|=m}((\mathcal{P}^n+\mathcal{N}^n)(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-(\mathcal{P}^n+\mathcal{N}^n)(\chi_{[\underline{i}]}\phi)(x_{\underline{j}(\underline{i})}))\\&\quad=\sum_{m=2}^n\sum_{|\underline{i}|=m}(\mathcal{N}^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\mathcal{N}^n(\chi_{[\underline{i}]}\phi)(x_{\underline{j}(\underline{i})})). \end{align*} $$
(The preceding expansion was not novel, and can be found for instance in [Reference Pollicott and SharpPS01, Lemma 3].) We now take the absolute value of both sides and observe that
![]() $d_\theta (x_{\underline {i}},x_{\underline {j}(\underline {i})}) =\theta ^{m-1}$
:
$d_\theta (x_{\underline {i}},x_{\underline {j}(\underline {i})}) =\theta ^{m-1}$
:
 $$ \begin{align*} &\bigg|\!\sum_{m=2}^n\sum_{|\underline{i}|=m}(\mathcal{N}^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\mathcal{N}^n(\chi_{[\underline{i}]}\phi)(x_{\underline{j}(\underline{i})}))\bigg|\\&\quad\leq \sum_{m=2}^n\sum_{|\underline{i}|=m}\|\mathcal{N}^n\chi_{[\underline{i}]}\phi\|_\theta\theta^{m-1}\leq\sum_{m=2}^n\|\mathcal{N}^{n-m}\|\sum_{|\underline{i}|=m}\|\mathcal{L}_\psi^m\chi_{[\underline{i}]}\phi\|_\theta\theta^{m-1}. \end{align*} $$
$$ \begin{align*} &\bigg|\!\sum_{m=2}^n\sum_{|\underline{i}|=m}(\mathcal{N}^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\mathcal{N}^n(\chi_{[\underline{i}]}\phi)(x_{\underline{j}(\underline{i})}))\bigg|\\&\quad\leq \sum_{m=2}^n\sum_{|\underline{i}|=m}\|\mathcal{N}^n\chi_{[\underline{i}]}\phi\|_\theta\theta^{m-1}\leq\sum_{m=2}^n\|\mathcal{N}^{n-m}\|\sum_{|\underline{i}|=m}\|\mathcal{L}_\psi^m\chi_{[\underline{i}]}\phi\|_\theta\theta^{m-1}. \end{align*} $$
In this last inequality, we made use of the fact that
![]() $\mathcal {N}\mathcal {P}=0$
to get the bound
$\mathcal {N}\mathcal {P}=0$
to get the bound
 $$ \begin{align*}\|\mathcal{N}^n(\chi_{[\underline{i}]}\phi)\|_\theta&=\|\mathcal{N}^{n-m}(\mathcal{N}^{m}(\chi_{[\underline{i}]}\phi)+\mathcal{P}^{m}(\chi_{[\underline{i}]}\phi))\|_\theta\\&= \|\mathcal{N}^{n-m}(\mathcal{L}_\psi^{m}(\chi_{[\underline{i}]}\phi))\|_\theta\leq \|\mathcal{N}^{n-m}\|\|\mathcal{L}_\psi^{m}(\chi_{[\underline{i}]}\phi))\|_\theta.\end{align*} $$
$$ \begin{align*}\|\mathcal{N}^n(\chi_{[\underline{i}]}\phi)\|_\theta&=\|\mathcal{N}^{n-m}(\mathcal{N}^{m}(\chi_{[\underline{i}]}\phi)+\mathcal{P}^{m}(\chi_{[\underline{i}]}\phi))\|_\theta\\&= \|\mathcal{N}^{n-m}(\mathcal{L}_\psi^{m}(\chi_{[\underline{i}]}\phi))\|_\theta\leq \|\mathcal{N}^{n-m}\|\|\mathcal{L}_\psi^{m}(\chi_{[\underline{i}]}\phi))\|_\theta.\end{align*} $$
We next estimate the term
![]() $\|\mathcal {L}_\psi ^{m}(\chi _{[\underline {i}]}\phi ))\|_\theta =\|e^{(S_m\psi )\circ \sigma _{\underline {i}}^{-1}}(\phi \circ \sigma _{\underline {i}}^{-1})\|_\theta $
, where
$\|\mathcal {L}_\psi ^{m}(\chi _{[\underline {i}]}\phi ))\|_\theta =\|e^{(S_m\psi )\circ \sigma _{\underline {i}}^{-1}}(\phi \circ \sigma _{\underline {i}}^{-1})\|_\theta $
, where
![]() $\sigma _{\underline {i}}^{-1}(x)=\underline {i}x$
is an inverse branch of
$\sigma _{\underline {i}}^{-1}(x)=\underline {i}x$
is an inverse branch of
![]() $\sigma ^n$
:
$\sigma ^n$
:
 $$ \begin{align*} &\|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}(\phi\circ\sigma_{\underline{i}}^{-1})\|_\theta= |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}(\phi\circ\sigma_{\underline{i}}^{-1})|_{\infty}+|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}(\phi\circ\sigma_{\underline{i}}^{-1})|_\theta\\&\quad\leq |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}|\phi|_{\infty}+|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}|(\phi\circ\sigma_{\underline{i}}^{-1})|_\theta+ |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_\theta|(\phi\circ\sigma_{\underline{i}}^{-1})|_{\infty}\\&\quad\leq |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}|\phi|_{\infty}+|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}|(\phi\circ\sigma_{\underline{i}}^{-1})|_\theta\\&\qquad+ |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}|S_m\psi\circ\sigma_{\underline{i}}^{-1}|_\theta|(\phi\circ\sigma_{\underline{i}}^{-1})|_{\infty}\\&\quad= |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty} ( |\phi|_{\infty}+|\phi\circ\sigma_{\underline{i}}^{-1}|_\theta +|S_m\psi\circ\sigma_{\underline{i}}^{-1}|_\theta|(\phi\circ\sigma_{\underline{i}}^{-1})|_{\infty})\\&\quad\leq |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty} ( \|\phi\|_{\theta}+ |\phi\circ\sigma_{\underline{i}}^{-1}|_\theta +|S_m\psi\circ\sigma_{\underline{i}}^{-1}|_\theta\|\phi\||_{\theta}). \end{align*} $$
$$ \begin{align*} &\|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}(\phi\circ\sigma_{\underline{i}}^{-1})\|_\theta= |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}(\phi\circ\sigma_{\underline{i}}^{-1})|_{\infty}+|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}(\phi\circ\sigma_{\underline{i}}^{-1})|_\theta\\&\quad\leq |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}|\phi|_{\infty}+|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}|(\phi\circ\sigma_{\underline{i}}^{-1})|_\theta+ |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_\theta|(\phi\circ\sigma_{\underline{i}}^{-1})|_{\infty}\\&\quad\leq |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}|\phi|_{\infty}+|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}|(\phi\circ\sigma_{\underline{i}}^{-1})|_\theta\\&\qquad+ |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}|S_m\psi\circ\sigma_{\underline{i}}^{-1}|_\theta|(\phi\circ\sigma_{\underline{i}}^{-1})|_{\infty}\\&\quad= |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty} ( |\phi|_{\infty}+|\phi\circ\sigma_{\underline{i}}^{-1}|_\theta +|S_m\psi\circ\sigma_{\underline{i}}^{-1}|_\theta|(\phi\circ\sigma_{\underline{i}}^{-1})|_{\infty})\\&\quad\leq |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty} ( \|\phi\|_{\theta}+ |\phi\circ\sigma_{\underline{i}}^{-1}|_\theta +|S_m\psi\circ\sigma_{\underline{i}}^{-1}|_\theta\|\phi\||_{\theta}). \end{align*} $$
To calculate the seminorms
![]() $|\phi \circ \sigma _{\underline {i}}^{-1}|_\theta $
and
$|\phi \circ \sigma _{\underline {i}}^{-1}|_\theta $
and
![]() $|S_m\psi \circ \sigma _{\underline {i}}^{-1}|_\theta $
, we use the fact that
$|S_m\psi \circ \sigma _{\underline {i}}^{-1}|_\theta $
, we use the fact that
![]() $\sigma _{\underline {i}}^{-1}$
is a
$\sigma _{\underline {i}}^{-1}$
is a
![]() $\theta ^m$
-contraction:
$\theta ^m$
-contraction:
 $$ \begin{align*} |S_m\psi\circ\sigma_{\underline{i}}^{-1}|_\theta&= \sup_{x\neq y}\frac{|S_m\psi\circ\sigma_{\underline{i}}^{-1}(x)-S_m\psi\circ\sigma_{\underline{i}}^{-1}(y)|}{d_\theta(x,y)}\\&\leq \sum_{i=0}^{m-1}\frac{|\psi(\sigma^i(\sigma_{\underline{i}}^{-1}(x)))-\psi(\sigma^i(\sigma_{\underline{i}}^{-1}(y)))|}{d_\theta(x,y)}\leq \sum_{i=0}^{m-1}|\psi|_\theta \theta^{m-i}{\kern-1pt}\leq{\kern-1pt}\frac{1}{1-\theta}|\psi|_\theta. \end{align*} $$
$$ \begin{align*} |S_m\psi\circ\sigma_{\underline{i}}^{-1}|_\theta&= \sup_{x\neq y}\frac{|S_m\psi\circ\sigma_{\underline{i}}^{-1}(x)-S_m\psi\circ\sigma_{\underline{i}}^{-1}(y)|}{d_\theta(x,y)}\\&\leq \sum_{i=0}^{m-1}\frac{|\psi(\sigma^i(\sigma_{\underline{i}}^{-1}(x)))-\psi(\sigma^i(\sigma_{\underline{i}}^{-1}(y)))|}{d_\theta(x,y)}\leq \sum_{i=0}^{m-1}|\psi|_\theta \theta^{m-i}{\kern-1pt}\leq{\kern-1pt}\frac{1}{1-\theta}|\psi|_\theta. \end{align*} $$
A similar (and simpler) calculation shows that
![]() $|\phi \circ \sigma _{\underline {i}}^{-1}|_\theta \leq \theta ^m\|\phi \|_\theta $
. Putting this all together, we find that
$|\phi \circ \sigma _{\underline {i}}^{-1}|_\theta \leq \theta ^m\|\phi \|_\theta $
. Putting this all together, we find that
 $$ \begin{align*}\|\mathcal{L}_\psi^m\chi_{[\underline{i}]}\phi\|_\theta\theta^{m-1}&\leq |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}\bigg( \|\phi\|_\theta\theta^{m-1}+\|\phi\|_\theta\theta^{2m-1}+ \frac{|\psi|_\theta}{1-\theta}\|\phi\|_\theta\theta^m\bigg)\\ & \leq C'|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}\|\phi\|_\theta\theta^m, \end{align*} $$
$$ \begin{align*}\|\mathcal{L}_\psi^m\chi_{[\underline{i}]}\phi\|_\theta\theta^{m-1}&\leq |e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}\bigg( \|\phi\|_\theta\theta^{m-1}+\|\phi\|_\theta\theta^{2m-1}+ \frac{|\psi|_\theta}{1-\theta}\|\phi\|_\theta\theta^m\bigg)\\ & \leq C'|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}\|\phi\|_\theta\theta^m, \end{align*} $$
where
![]() $C'=\max \{1,{|\psi |_\theta }/({1-\theta })\}$
. Thus, using the spectral radius bound for
$C'=\max \{1,{|\psi |_\theta }/({1-\theta })\}$
. Thus, using the spectral radius bound for
![]() $\mathcal {N}$
, we find that
$\mathcal {N}$
, we find that
 $$ \begin{align*} &\sum_{m=2}^n\|\mathcal{N}^{n-m}\|\sum_{|\underline{i}|=m}\|\mathcal{L}_\psi^m\chi_{[\underline{i}]}\phi\|_\theta\theta^{m-1}\\ &\quad\leq \sum_{m=2}^nC(r+\varepsilon)^{n-m}e^{(n-m)P(\psi)}C'\theta^m\|\phi\|_\theta\sum_{|\underline{i}|=m}|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}\\ &\quad\leq C"\|\phi\|_\theta\kappa^n\sum_{m=2}^ne^{(n-m)P(\psi)}\sum_{|\underline{i}|=m}|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}, \end{align*} $$
$$ \begin{align*} &\sum_{m=2}^n\|\mathcal{N}^{n-m}\|\sum_{|\underline{i}|=m}\|\mathcal{L}_\psi^m\chi_{[\underline{i}]}\phi\|_\theta\theta^{m-1}\\ &\quad\leq \sum_{m=2}^nC(r+\varepsilon)^{n-m}e^{(n-m)P(\psi)}C'\theta^m\|\phi\|_\theta\sum_{|\underline{i}|=m}|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}\\ &\quad\leq C"\|\phi\|_\theta\kappa^n\sum_{m=2}^ne^{(n-m)P(\psi)}\sum_{|\underline{i}|=m}|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}, \end{align*} $$
where
![]() $\kappa =\max \{\theta ,r+\varepsilon \}<1$
. We have seen previously that
$\kappa =\max \{\theta ,r+\varepsilon \}<1$
. We have seen previously that
![]() $|S_m\psi \circ \sigma _{\underline {i}}^{-1}(x)-S_m\psi \circ \sigma _{\underline {i}}^{-1}(y)|\leq ({|\psi |_\theta }/({1-\theta }))\,d_\theta (x,y)\leq K<\infty $
(since the diameter of
$|S_m\psi \circ \sigma _{\underline {i}}^{-1}(x)-S_m\psi \circ \sigma _{\underline {i}}^{-1}(y)|\leq ({|\psi |_\theta }/({1-\theta }))\,d_\theta (x,y)\leq K<\infty $
(since the diameter of
![]() $\Sigma _A^+$
is finite). Taking the exponential of both sides, we obtain the following bounded distortion estimate:
$\Sigma _A^+$
is finite). Taking the exponential of both sides, we obtain the following bounded distortion estimate:
for any
![]() $x,y$
in the domain of
$x,y$
in the domain of
![]() $\sigma _{\underline {i}}^{-1}$
. Notice that the domain of
$\sigma _{\underline {i}}^{-1}$
. Notice that the domain of
![]() $\sigma _{\underline {i}}^{-1}$
is completely determined by the last symbol in the string
$\sigma _{\underline {i}}^{-1}$
is completely determined by the last symbol in the string
![]() $\underline {i}$
. For each
$\underline {i}$
. For each
![]() $\underline {i}$
, let
$\underline {i}$
, let
![]() $y_{\underline {i}}$
be such that
$y_{\underline {i}}$
be such that
![]() $e^{(S_m\psi )\circ \sigma _{\underline {i}}^{-1}(y_{\underline {i}})}=|e^{(S_m\psi )\circ \sigma _{\underline {i}}^{-1}}|_{\infty }$
, and let
$e^{(S_m\psi )\circ \sigma _{\underline {i}}^{-1}(y_{\underline {i}})}=|e^{(S_m\psi )\circ \sigma _{\underline {i}}^{-1}}|_{\infty }$
, and let
![]() $z_{\underline {i}}$
be any point in the domain of
$z_{\underline {i}}$
be any point in the domain of
![]() $\sigma _{\underline {i}}^{-1}$
that only depends on the last symbol
$\sigma _{\underline {i}}^{-1}$
that only depends on the last symbol
![]() $i_{m}$
. Then,
$i_{m}$
. Then,
 $$ \begin{align*} \sum_{|\underline{i}|=m}|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}&\leq C\sum_{|\underline{i}|=m}e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}(z_{\underline{i}})}\\&=C\sum_{i_m=1}^m\mathcal{L}_\psi^m1(z_{\underline{i}})\leq Cm\|\mathcal{L}_\psi^m 1\|_\theta\leq Ce^{m(P(\psi)+\varepsilon)}. \end{align*} $$
$$ \begin{align*} \sum_{|\underline{i}|=m}|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}&\leq C\sum_{|\underline{i}|=m}e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}(z_{\underline{i}})}\\&=C\sum_{i_m=1}^m\mathcal{L}_\psi^m1(z_{\underline{i}})\leq Cm\|\mathcal{L}_\psi^m 1\|_\theta\leq Ce^{m(P(\psi)+\varepsilon)}. \end{align*} $$
Therefore,
 $$ \begin{align} &\bigg|\!\sum_{|\underline{i}|=n}\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg|\nonumber\\&\quad\leq C"\|\phi\|_\theta\kappa^n\sum_{m=2}^ne^{(n-m)P(\psi)}\sum_{|\underline{i}|=m}|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}\nonumber\\&\quad\leq C"'\|\phi\|_\theta\kappa^ne^{n(P(\psi)+\varepsilon)}(n-2)\leq C"'\|\phi\|_\theta(\kappa+\varepsilon)^ne^{n(P(\psi)+\varepsilon)}. \end{align} $$
$$ \begin{align} &\bigg|\!\sum_{|\underline{i}|=n}\mathcal{L}_\psi^n(\chi_{[\underline{i}]}\phi)(x_{\underline{i}})-\sum_{k=1}^m\mathcal{L}_\psi^n(\chi_{[i]}\phi)(x_i)\bigg|\nonumber\\&\quad\leq C"\|\phi\|_\theta\kappa^n\sum_{m=2}^ne^{(n-m)P(\psi)}\sum_{|\underline{i}|=m}|e^{(S_m\psi)\circ\sigma_{\underline{i}}^{-1}}|_{\infty}\nonumber\\&\quad\leq C"'\|\phi\|_\theta\kappa^ne^{n(P(\psi)+\varepsilon)}(n-2)\leq C"'\|\phi\|_\theta(\kappa+\varepsilon)^ne^{n(P(\psi)+\varepsilon)}. \end{align} $$
Combining the estimates in equations (3.2), (3.3), and (3.4), we have shown
 $$ \begin{align*} \bigg|\!\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)\bigg|\leq C\|\phi\|_\theta(\kappa+\varepsilon)^ne^{n(P(\psi)+\varepsilon)} \end{align*} $$
$$ \begin{align*} \bigg|\!\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)\bigg|\leq C\|\phi\|_\theta(\kappa+\varepsilon)^ne^{n(P(\psi)+\varepsilon)} \end{align*} $$
with
![]() $\kappa +\varepsilon <1$
. We therefore have
$\kappa +\varepsilon <1$
. We therefore have
 $$ \begin{align*} \bigg|\frac{1}{Z_n}\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)\bigg|\leq De^{-nP(\psi)}C\|\phi\|_\theta(\kappa+\varepsilon)^ne^{n(P(\psi)+\varepsilon)}\leq C\|\phi\|_\theta(\kappa+\varepsilon)^ne^{n\varepsilon}. \end{align*} $$
$$ \begin{align*} \bigg|\frac{1}{Z_n}\sum_{\sigma^n(x)=x}e^{S_n\psi(x)}\phi(x)\bigg|\leq De^{-nP(\psi)}C\|\phi\|_\theta(\kappa+\varepsilon)^ne^{n(P(\psi)+\varepsilon)}\leq C\|\phi\|_\theta(\kappa+\varepsilon)^ne^{n\varepsilon}. \end{align*} $$
Finally, letting
![]() $\tau =(\kappa +\varepsilon )e^\varepsilon <1$
for sufficiently small
$\tau =(\kappa +\varepsilon )e^\varepsilon <1$
for sufficiently small
![]() $\varepsilon>0$
, this gives equation (3.1).
$\varepsilon>0$
, this gives equation (3.1).
Remark 5. By standard arguments, it is easy to deduce the same equidistribution result for two-sided shifts.
To pass to the proof of Theorem 2.3, we will use Markov partitions. It is well known that repellers and Axiom A diffeomorphisms admit finite Markov partitions; see Przytycki and Urbanski [Reference Przytycki and UrbanskiPU10, Theorem 3.5.2] in the case of expanding maps and Bowen [Reference BowenBow70] for the case of Axiom A diffeomorphisms. More precisely, if
![]() $(J,T)$
is a repeller or
$(J,T)$
is a repeller or
![]() $(\Omega (T),T)$
is an Axiom A diffeomorphism, then there exists a subshift of finite type
$(\Omega (T),T)$
is an Axiom A diffeomorphism, then there exists a subshift of finite type
![]() $(\Sigma _A^+,\sigma )$
and a semiconjugacy
$(\Sigma _A^+,\sigma )$
and a semiconjugacy
![]() $\pi :\Sigma _A^+\rightarrow J$
(respectively
$\pi :\Sigma _A^+\rightarrow J$
(respectively
![]() $(\Sigma _A,\sigma )$
for
$(\Sigma _A,\sigma )$
for
![]() $(\Omega (T),T)$
). If the transformation T is mixing, then the transition matrix A is irreducible and aperiodic. For an appropriately chosen
$(\Omega (T),T)$
). If the transformation T is mixing, then the transition matrix A is irreducible and aperiodic. For an appropriately chosen
![]() $\theta $
, Lipschitz functions f defined on J or
$\theta $
, Lipschitz functions f defined on J or
![]() $\Omega (T)$
can be lifted to a Lipschitz function
$\Omega (T)$
can be lifted to a Lipschitz function
![]() $f\circ \pi $
. We proceed to prove Theorem 2.3 in the case of one-dimensional expanding maps, where the passage to a Markov partition is simplest. However, to obtain a uniform effective equidistribution for expanding maps, we need uniform effective equidistribution of corresponding lifted systems in Theorem 3.2. Uniformity is lost in Theorem 3.2 when we apply the spectral radius formula to get bounds on
$f\circ \pi $
. We proceed to prove Theorem 2.3 in the case of one-dimensional expanding maps, where the passage to a Markov partition is simplest. However, to obtain a uniform effective equidistribution for expanding maps, we need uniform effective equidistribution of corresponding lifted systems in Theorem 3.2. Uniformity is lost in Theorem 3.2 when we apply the spectral radius formula to get bounds on
![]() $\|\mathcal {N}^n\|_\theta $
. However, for the particular systems we are considering, we can obtain uniform bounds on
$\|\mathcal {N}^n\|_\theta $
. However, for the particular systems we are considering, we can obtain uniform bounds on
![]() $\|\mathcal {N}^n\|_\theta $
by using the Birkhoff cone technique, adapted to subshifts of finite type by Naud in [Reference NaudNau04].
$\|\mathcal {N}^n\|_\theta $
by using the Birkhoff cone technique, adapted to subshifts of finite type by Naud in [Reference NaudNau04].
Lemma 3.3. There exists
![]() $C_{\mathcal {W}}>0$
and
$C_{\mathcal {W}}>0$
and
![]() $0<\tau _{\mathcal {W}}<1$
such that the following is true. Given
$0<\tau _{\mathcal {W}}<1$
such that the following is true. Given
![]() $f\in \mathcal {W}$
, let
$f\in \mathcal {W}$
, let
![]() $\pi _f$
be the associated semiconjugacy to the full shift on
$\pi _f$
be the associated semiconjugacy to the full shift on
![]() $\deg (f)$
-symbols, and let
$\deg (f)$
-symbols, and let
![]() $\psi _f=-\log (f'\circ \pi _f)$
. If
$\psi _f=-\log (f'\circ \pi _f)$
. If
![]() $\mathcal {L}_{\psi _f}h_f= e^{P(\psi _f)}h_f$
, we consider the normalized potential
$\mathcal {L}_{\psi _f}h_f= e^{P(\psi _f)}h_f$
, we consider the normalized potential
![]() $\overline {\psi }_f=\psi _f+\log (h_f)-\log (h_f\circ \sigma )$
. Then, for all
$\overline {\psi }_f=\psi _f+\log (h_f)-\log (h_f\circ \sigma )$
. Then, for all
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\|\mathcal {N}_{\overline {\psi }_f}^n\|_\theta < C_{\mathcal {W}}\tau _{\mathcal {W}}^ne^{nP(\overline {\psi }_f)}$
.
$\|\mathcal {N}_{\overline {\psi }_f}^n\|_\theta < C_{\mathcal {W}}\tau _{\mathcal {W}}^ne^{nP(\overline {\psi }_f)}$
.
We review the Birkhoff cone construction and prove Lemma 3.3 in Appendix A.
Proof of Theorem 2.3
Consider a degree k expanding map
![]() $f:S^1\rightarrow S^1$
. Then, the Markov partition of
$f:S^1\rightarrow S^1$
. Then, the Markov partition of
![]() $(f,S^1)$
consists of k closed intervals which are each mapped under f to the entirety of
$(f,S^1)$
consists of k closed intervals which are each mapped under f to the entirety of
![]() $S^1$
. Consequentially,
$S^1$
. Consequentially,
![]() $(f, S^1)$
is semiconjugated to the full shift on k symbols,
$(f, S^1)$
is semiconjugated to the full shift on k symbols,
![]() $(\sigma , \Sigma ^+)$
. Let
$(\sigma , \Sigma ^+)$
. Let
![]() $\phi :S^1\rightarrow \mathbb {C}$
be a Lipschitz function. We can then lift
$\phi :S^1\rightarrow \mathbb {C}$
be a Lipschitz function. We can then lift
![]() $\phi $
to a Lipschitz function
$\phi $
to a Lipschitz function
![]() $\phi \circ \pi :\Sigma ^+\rightarrow \mathbb {C}$
. Likewise, let
$\phi \circ \pi :\Sigma ^+\rightarrow \mathbb {C}$
. Likewise, let
![]() $\psi _f:S^1\rightarrow \mathbb {C}$
be the geometric potential with equilibrium state
$\psi _f:S^1\rightarrow \mathbb {C}$
be the geometric potential with equilibrium state
![]() $\mu _f$
, and let
$\mu _f$
, and let
![]() $\psi _f\circ \pi :\Sigma ^+\rightarrow \mathbb {C}$
be the lifted potential with equilibrium state
$\psi _f\circ \pi :\Sigma ^+\rightarrow \mathbb {C}$
be the lifted potential with equilibrium state
![]() $\mu _{\psi _f\circ \pi }$
. We claim that the pushforward of
$\mu _{\psi _f\circ \pi }$
. We claim that the pushforward of
![]() $\mu _{\psi _f\circ \pi }$
under
$\mu _{\psi _f\circ \pi }$
under
![]() $\pi $
is
$\pi $
is
![]() $\mu _{f}$
, that is,
$\mu _{f}$
, that is,
![]() $\pi _*\mu _{\psi _f\circ \pi }=\mu _{f}$
. Unfortunately, it is not true that
$\pi _*\mu _{\psi _f\circ \pi }=\mu _{f}$
. Unfortunately, it is not true that
![]() $\pi _*\mu _{\psi _f\circ \pi }^n=\mu _{f}^n$
. Since the semiconjugacy is not injective, we may have multiple distinct periodic orbits for
$\pi _*\mu _{\psi _f\circ \pi }^n=\mu _{f}^n$
. Since the semiconjugacy is not injective, we may have multiple distinct periodic orbits for
![]() $(\Sigma ^+,\sigma )$
get mapped under
$(\Sigma ^+,\sigma )$
get mapped under
![]() $\pi $
to the same periodic orbit of
$\pi $
to the same periodic orbit of
![]() $(S^1,f)$
.
$(S^1,f)$
.
We know that
![]() $|\operatorname {\mathrm {Fix}}(\sigma ^n)|=k^n$
and
$|\operatorname {\mathrm {Fix}}(\sigma ^n)|=k^n$
and
![]() $|\operatorname {\mathrm {Fix}}(f^n)|=k^n-1$
. Moreover, distinct periodic orbits of f can be lifted to distinct periodic orbits of
$|\operatorname {\mathrm {Fix}}(f^n)|=k^n-1$
. Moreover, distinct periodic orbits of f can be lifted to distinct periodic orbits of
![]() $\sigma $
with the same period, so we have that for each n, only two distinct points of
$\sigma $
with the same period, so we have that for each n, only two distinct points of
![]() $\Sigma ^+$
of period n get mapped under
$\Sigma ^+$
of period n get mapped under
![]() $\pi $
to the same point. Let
$\pi $
to the same point. Let
![]() $\nu _{\psi _f\circ \pi }^n$
be any measure on
$\nu _{\psi _f\circ \pi }^n$
be any measure on
![]() $\Sigma ^+$
such that
$\Sigma ^+$
such that
![]() $\pi ^*\nu _{\psi _f\circ \pi }^n=\mu _{f}^n$
. Then,
$\pi ^*\nu _{\psi _f\circ \pi }^n=\mu _{f}^n$
. Then,
 $$ \begin{align} &\bigg|\!\int\phi \,d\mu_f^n-\int\phi \,d\mu_f\bigg|= \bigg|\!\int\phi\circ\pi d\nu_{\psi\circ\pi}^n-\int\phi\circ\pi \,d\mu_{\psi_f\circ\pi}\bigg|\nonumber\\ &\quad\leq\bigg|\!\int\phi\circ\pi \,d\mu_{\psi_f\circ\pi}^n-\int\phi\circ\pi \,d\mu_{\psi_f\circ\pi}\bigg|+ \bigg|\!\int\phi\circ\pi d\nu_{\psi_f\circ\pi}^n-\int\phi\circ\pi \,d\mu_{\psi_f\circ\pi}^n\bigg|. \end{align} $$
$$ \begin{align} &\bigg|\!\int\phi \,d\mu_f^n-\int\phi \,d\mu_f\bigg|= \bigg|\!\int\phi\circ\pi d\nu_{\psi\circ\pi}^n-\int\phi\circ\pi \,d\mu_{\psi_f\circ\pi}\bigg|\nonumber\\ &\quad\leq\bigg|\!\int\phi\circ\pi \,d\mu_{\psi_f\circ\pi}^n-\int\phi\circ\pi \,d\mu_{\psi_f\circ\pi}\bigg|+ \bigg|\!\int\phi\circ\pi d\nu_{\psi_f\circ\pi}^n-\int\phi\circ\pi \,d\mu_{\psi_f\circ\pi}^n\bigg|. \end{align} $$
The first term in equation (3.5) can be bounded by
![]() $C\|\phi \circ \pi \|_\theta \tau ^n$
using Theorem 3.2. To estimate the last term of equation (3.5), we write
$C\|\phi \circ \pi \|_\theta \tau ^n$
using Theorem 3.2. To estimate the last term of equation (3.5), we write
 $$ \begin{align*} \nu_{\psi_f\circ\pi}^n=\frac{1}{Z_n(\psi_f)}\sum_{x\in A_n} e^{S_n(\psi_f)(\pi(x))}\delta_x, \end{align*} $$
$$ \begin{align*} \nu_{\psi_f\circ\pi}^n=\frac{1}{Z_n(\psi_f)}\sum_{x\in A_n} e^{S_n(\psi_f)(\pi(x))}\delta_x, \end{align*} $$
where
![]() $A_n$
is any subset of
$A_n$
is any subset of
![]() $\operatorname {\mathrm {Fix}}(\sigma ^n)$
that is mapped bijectively to
$\operatorname {\mathrm {Fix}}(\sigma ^n)$
that is mapped bijectively to
![]() $\operatorname {\mathrm {Fix}}(f^n)$
, and
$\operatorname {\mathrm {Fix}}(f^n)$
, and
![]() $Z_n({\psi })$
is a normalization constant. Then, if we let
$Z_n({\psi })$
is a normalization constant. Then, if we let
![]() $y\in \operatorname {\mathrm {Fix}}(\sigma ^n)/A_n$
, we have
$y\in \operatorname {\mathrm {Fix}}(\sigma ^n)/A_n$
, we have
 $$ \begin{align*} &\bigg|\!\int\phi\circ\pi d\nu_{\psi_f\circ\pi}^n-\int\phi\circ\pi \,d\mu_{\psi_f\circ\pi}^n\bigg|\\& \quad=\bigg|\frac{1}{Z_n(\psi_f)}\sum_{x\in A_n} e^{S_n(\psi_f)(\pi(x))}\phi(\pi(x))-\frac{1}{Z_n(\psi_f\circ\pi)}\sum_{x\in \operatorname{\mathrm{Fix}}(\sigma^n)} e^{S_n(\psi_f)(\pi(x))}\phi(\pi(x))\bigg|\\ &\quad\leq\bigg|\bigg(\frac{1}{Z_n(\psi_f)}-\frac{1}{Z_n(\psi_f\circ\pi)}\bigg)\sum_{x\in \operatorname{\mathrm{Fix}}(\sigma^n)} e^{S_n(\psi_f)(\pi(x))}\phi(\pi(x))\bigg|\\ &\qquad+\frac{1}{Z_n(\psi_f)}\bigg|\sum_{x\in A_n} e^{S_n(\psi_f)(\pi(x))}\phi(\pi(x))-\sum_{x\in \operatorname{\mathrm{Fix}}(\sigma^n)} e^{S_n(\psi_f)(\pi(x))}\phi(\pi(x))\bigg|\\ &\quad\leq\bigg(\frac{Z_n(\psi_f\circ\pi)}{Z_n(\psi_f)}-1\bigg)\|\phi\circ\pi\|_{\infty}+\frac{1}{Z_n(\psi_f)}e^{S_n(\psi_f)(\pi(y))}|\phi(\pi(y))|\\ &\quad\leq\bigg(\frac{Z_n(\psi_f)+e^{S_n(\psi_f)(\pi(y))}}{Z_n(\psi_f)}-1\bigg)\|\phi\circ\pi\|_{\infty}+\frac{1}{Z_n(\psi_f)}e^{S_n(\psi_f)(\pi(y))}|\phi(\pi(y))|\\ &\quad\leq\frac{2}{Z_n(\psi_f)}e^{S_n(\psi_f)(\pi(y))}\|\phi\circ\pi\|_{\theta}\leq D\|\phi\circ\pi\|_{\theta}e^{S_n(\psi_f)(\pi(y))}e^{-nP(\psi_f)}. \end{align*} $$
$$ \begin{align*} &\bigg|\!\int\phi\circ\pi d\nu_{\psi_f\circ\pi}^n-\int\phi\circ\pi \,d\mu_{\psi_f\circ\pi}^n\bigg|\\& \quad=\bigg|\frac{1}{Z_n(\psi_f)}\sum_{x\in A_n} e^{S_n(\psi_f)(\pi(x))}\phi(\pi(x))-\frac{1}{Z_n(\psi_f\circ\pi)}\sum_{x\in \operatorname{\mathrm{Fix}}(\sigma^n)} e^{S_n(\psi_f)(\pi(x))}\phi(\pi(x))\bigg|\\ &\quad\leq\bigg|\bigg(\frac{1}{Z_n(\psi_f)}-\frac{1}{Z_n(\psi_f\circ\pi)}\bigg)\sum_{x\in \operatorname{\mathrm{Fix}}(\sigma^n)} e^{S_n(\psi_f)(\pi(x))}\phi(\pi(x))\bigg|\\ &\qquad+\frac{1}{Z_n(\psi_f)}\bigg|\sum_{x\in A_n} e^{S_n(\psi_f)(\pi(x))}\phi(\pi(x))-\sum_{x\in \operatorname{\mathrm{Fix}}(\sigma^n)} e^{S_n(\psi_f)(\pi(x))}\phi(\pi(x))\bigg|\\ &\quad\leq\bigg(\frac{Z_n(\psi_f\circ\pi)}{Z_n(\psi_f)}-1\bigg)\|\phi\circ\pi\|_{\infty}+\frac{1}{Z_n(\psi_f)}e^{S_n(\psi_f)(\pi(y))}|\phi(\pi(y))|\\ &\quad\leq\bigg(\frac{Z_n(\psi_f)+e^{S_n(\psi_f)(\pi(y))}}{Z_n(\psi_f)}-1\bigg)\|\phi\circ\pi\|_{\infty}+\frac{1}{Z_n(\psi_f)}e^{S_n(\psi_f)(\pi(y))}|\phi(\pi(y))|\\ &\quad\leq\frac{2}{Z_n(\psi_f)}e^{S_n(\psi_f)(\pi(y))}\|\phi\circ\pi\|_{\theta}\leq D\|\phi\circ\pi\|_{\theta}e^{S_n(\psi_f)(\pi(y))}e^{-nP(\psi_f)}. \end{align*} $$
In the case of expanding maps, we have that
![]() $P(\psi _f)=0$
and
$P(\psi _f)=0$
and
![]() $S_n(\psi _f)(\pi (y))\leq -n\log \unicode{x3bb} _f$
, where
$S_n(\psi _f)(\pi (y))\leq -n\log \unicode{x3bb} _f$
, where
![]() $\unicode{x3bb} _f>1$
is the expansion constant for f, that is,
$\unicode{x3bb} _f>1$
is the expansion constant for f, that is,
![]() $|f'(x)|\geq \unicode{x3bb} _f$
for all
$|f'(x)|\geq \unicode{x3bb} _f$
for all
![]() $x\in S^1$
. This proves that
$x\in S^1$
. This proves that
 $$ \begin{align*} \bigg|\!\int\phi \,d\mu_f^n-\int\phi \,d\mu_f\bigg|\leq C'\|\phi\circ\pi\|_{\theta}\tau^n \end{align*} $$
$$ \begin{align*} \bigg|\!\int\phi \,d\mu_f^n-\int\phi \,d\mu_f\bigg|\leq C'\|\phi\circ\pi\|_{\theta}\tau^n \end{align*} $$
for some
![]() $0<\tau <1$
(not necessarily the same
$0<\tau <1$
(not necessarily the same
![]() $\tau $
as in Theorem 3.2). Clearly,
$\tau $
as in Theorem 3.2). Clearly,
![]() $\|\phi \circ \pi \|_{\infty }\leq \|\phi \|_{\infty }$
. Moreover,
$\|\phi \circ \pi \|_{\infty }\leq \|\phi \|_{\infty }$
. Moreover,
 $$ \begin{align*}|\phi\circ\pi|_{\theta}=\sup_{x\neq y}\frac{|\phi(\pi(x)-\phi(\pi(y))|}{d_\theta(x,y)}\leq |\phi|_{\mathrm{Lip}}\frac{d(\pi(x),\pi(y))}{d_\theta(x,y)}\leq |\pi|_\theta|\phi|_{\mathrm{Lip}},\end{align*} $$
$$ \begin{align*}|\phi\circ\pi|_{\theta}=\sup_{x\neq y}\frac{|\phi(\pi(x)-\phi(\pi(y))|}{d_\theta(x,y)}\leq |\phi|_{\mathrm{Lip}}\frac{d(\pi(x),\pi(y))}{d_\theta(x,y)}\leq |\pi|_\theta|\phi|_{\mathrm{Lip}},\end{align*} $$
so that
![]() $\|\phi \circ \pi \|_\theta \leq \max \{1,|\pi |_{\theta }\}\|\phi \|_{\mathrm {Lip}}.$
Thus, absorbing all constants into C, we have
$\|\phi \circ \pi \|_\theta \leq \max \{1,|\pi |_{\theta }\}\|\phi \|_{\mathrm {Lip}}.$
Thus, absorbing all constants into C, we have
 $$ \begin{align*}\bigg|\int\phi \,d\mu_f^n-\int\phi \,d\mu_f\bigg|\leq C\|\phi\|_{\mathrm{Lip}}\tau^N, \end{align*} $$
$$ \begin{align*}\bigg|\int\phi \,d\mu_f^n-\int\phi \,d\mu_f\bigg|\leq C\|\phi\|_{\mathrm{Lip}}\tau^N, \end{align*} $$
as desired.
Remark 6. One can prove effective equidistribution for general expanding repellers and Axiom A diffeomorphism using Markov partitions in the same way, but more care is needed to handle the difference between the measure
![]() $\nu _{\psi _f\circ \pi }^n$
and
$\nu _{\psi _f\circ \pi }^n$
and
![]() $\mu _{\psi _f\circ \pi }^n$
.
$\mu _{\psi _f\circ \pi }^n$
.
Acknowledgments
The author would like to express his sincerest thanks to Andrey Gogolev for suggesting the problem, and for his patience and invaluable guidance. The author would also like to thank James Marshall Reber for many useful discussions and for his help in proving Theorem 3.2. Thanks to Daniel Smania for providing valuable comments on the draft of this paper. Finally, the author would like to express his gratitude to the referee for their comments which greatly helped with the readability of the present paper.
A. Appendix. Birkhoff cones for subshifts of finite type
Rather than deducing our desired bounds on
![]() $\|\mathcal {N}_{\psi _f}^n\|_\theta $
as a consequence of quasi-compactness of the transfer operator (the standard approach of the Ruelle–Perron–Frobenius theorem), we use the technique of Birkhoff cones. The idea is to show that the transfer operator contracts a certain cone of Lipschitz functions with respect to a ‘pseudo-metric’ and to then establish the leading eigenfunction as a fixed point with respect to this pseudo-metric. The benefit to this approach is that we can establish explicit bounds on
$\|\mathcal {N}_{\psi _f}^n\|_\theta $
as a consequence of quasi-compactness of the transfer operator (the standard approach of the Ruelle–Perron–Frobenius theorem), we use the technique of Birkhoff cones. The idea is to show that the transfer operator contracts a certain cone of Lipschitz functions with respect to a ‘pseudo-metric’ and to then establish the leading eigenfunction as a fixed point with respect to this pseudo-metric. The benefit to this approach is that we can establish explicit bounds on
![]() $\|\mathcal {N}_{\psi _f}^n\|_\theta $
which will be uniform in our set
$\|\mathcal {N}_{\psi _f}^n\|_\theta $
which will be uniform in our set
![]() $\mathcal {W}$
. Then, one can actually deduce quasi-compactness as a consequence of this bound. This approach is standard for uniformly expanding maps; see Baladi [Reference BaladiBal00, §2.2]. For subshifts of finite type, we follow Naud [Reference NaudNau04] closely, applied to the specific case of the full shift that we need, and for which certain technical difficulties vanish.
$\mathcal {W}$
. Then, one can actually deduce quasi-compactness as a consequence of this bound. This approach is standard for uniformly expanding maps; see Baladi [Reference BaladiBal00, §2.2]. For subshifts of finite type, we follow Naud [Reference NaudNau04] closely, applied to the specific case of the full shift that we need, and for which certain technical difficulties vanish.
Definition A.1. A subset
![]() $\Lambda \subset \mathcal {B}/\{0\}$
of a Banach space
$\Lambda \subset \mathcal {B}/\{0\}$
of a Banach space
![]() $\mathcal {B}$
is called a cone if
$\mathcal {B}$
is called a cone if
![]() $\unicode{x3bb} \phi \in \Lambda $
for all
$\unicode{x3bb} \phi \in \Lambda $
for all
![]() $\phi \in \Lambda $
and all
$\phi \in \Lambda $
and all
![]() $\unicode{x3bb}>0$
. The cone is called closed if
$\unicode{x3bb}>0$
. The cone is called closed if
![]() $\Lambda \cup \{0\}$
is closed, and
$\Lambda \cup \{0\}$
is closed, and
![]() $\Lambda $
is called convex if
$\Lambda $
is called convex if
![]() $\psi _1+\psi _2\in \Lambda $
for every
$\psi _1+\psi _2\in \Lambda $
for every
![]() $\psi _1,\psi _2\in \Lambda $
. A cone
$\psi _1,\psi _2\in \Lambda $
. A cone
![]() $\Lambda $
induces a partial order
$\Lambda $
induces a partial order
![]() $\leq _\Lambda $
on
$\leq _\Lambda $
on
![]() $\mathcal {B}$
by defining
$\mathcal {B}$
by defining
![]() $\psi \leq _\Lambda \phi \iff \phi -\psi \in \Lambda \cup \{0\}$
.
$\psi \leq _\Lambda \phi \iff \phi -\psi \in \Lambda \cup \{0\}$
.
Definition A.2. For
![]() $\psi $
and
$\psi $
and
![]() $\phi $
in a cone
$\phi $
in a cone
![]() $\Lambda $
, define
$\Lambda $
, define
Then, we define the Hilbert pseudo-metric
![]() $\Theta _\Lambda $
on
$\Theta _\Lambda $
on
![]() $\unicode{x3bb} $
by
$\unicode{x3bb} $
by
Theorem A.1. (Birkhoff’s inequality)
Let
![]() $\Lambda $
be a convex cone in a Banach space
$\Lambda $
be a convex cone in a Banach space
![]() $\mathcal {B}$
. If
$\mathcal {B}$
. If
![]() $T:\mathcal {B}\rightarrow \mathcal {B}$
is a linear operator such that
$T:\mathcal {B}\rightarrow \mathcal {B}$
is a linear operator such that
![]() $T(\Lambda )\subset \Lambda $
, then for each
$T(\Lambda )\subset \Lambda $
, then for each
![]() $\phi ,\psi \in \Lambda $
, we have
$\phi ,\psi \in \Lambda $
, we have
 $$ \begin{align*} \Theta_\Lambda(T\phi,T\psi)\leq \tanh\bigg({\frac{\operatorname{\mathrm{diam}}_{\Theta_\Lambda}(T\Lambda)}{4}}\bigg)\Theta_\Lambda(\phi,\psi). \end{align*} $$
$$ \begin{align*} \Theta_\Lambda(T\phi,T\psi)\leq \tanh\bigg({\frac{\operatorname{\mathrm{diam}}_{\Theta_\Lambda}(T\Lambda)}{4}}\bigg)\Theta_\Lambda(\phi,\psi). \end{align*} $$
Lemma A.2. Let
![]() $\Lambda $
be a closed convex cone in a Banach space
$\Lambda $
be a closed convex cone in a Banach space
![]() $\mathcal {B}$
endowed with two (not necessarily equivalent norms
$\mathcal {B}$
endowed with two (not necessarily equivalent norms
![]() $\|\cdot \|_i$
,
$\|\cdot \|_i$
,
![]() $i=1,2,$
and assume that for all
$i=1,2,$
and assume that for all
![]() $\phi ,\psi \in \mathcal {B}$
,
$\phi ,\psi \in \mathcal {B}$
,
Then, for any
![]() $\phi ,\psi \in \Lambda $
with
$\phi ,\psi \in \Lambda $
with
![]() $\|\phi \|_1=\|\psi \|_1$
, we have
$\|\phi \|_1=\|\psi \|_1$
, we have
If
![]() $\Sigma ^+$
is the one-sided full shift on k-symbols, and if
$\Sigma ^+$
is the one-sided full shift on k-symbols, and if
![]() $\mathcal {F}_\theta ^+$
is the Banach space of Lipschitz continuous functions on
$\mathcal {F}_\theta ^+$
is the Banach space of Lipschitz continuous functions on
![]() $\Sigma ^+$
with respect to the
$\Sigma ^+$
with respect to the
![]() $d_\theta $
-metric, then given any
$d_\theta $
-metric, then given any
![]() $L>0$
, we have a cone in
$L>0$
, we have a cone in
![]() $\mathcal {F}_\theta ^+$
given by
$\mathcal {F}_\theta ^+$
given by
To apply Birkhoff’s inequality, we will need the following lemmas.
Lemma A.3. Fix
![]() $0<\xi <1$
. Then, for every
$0<\xi <1$
. Then, for every
![]() $\phi ,\psi \in \mathcal {C}_{\xi L}$
with
$\phi ,\psi \in \mathcal {C}_{\xi L}$
with
![]() $\phi ,\psi>0$
, we have
$\phi ,\psi>0$
, we have
 $$ \begin{align*} \Theta_{L}(\phi,\psi)\leq 2\log\bigg(\frac{1+\xi}{1-\xi}\bigg)+\log\sup_{x,y\in\Sigma^+}\bigg(\frac{\phi(x)\psi(y)}{\phi(y)\psi(x)}\bigg). \end{align*} $$
$$ \begin{align*} \Theta_{L}(\phi,\psi)\leq 2\log\bigg(\frac{1+\xi}{1-\xi}\bigg)+\log\sup_{x,y\in\Sigma^+}\bigg(\frac{\phi(x)\psi(y)}{\phi(y)\psi(x)}\bigg). \end{align*} $$
See Naud [Reference NaudNau04, Proposition 5.3] for the proof, which is unchanged in our setting.
Lemma A.4. Fix
![]() $\theta <\xi <1$
. Then, for every
$\theta <\xi <1$
. Then, for every
![]() $L\geq {\theta |\psi |_\theta }/({\xi -\theta })$
, we have
$L\geq {\theta |\psi |_\theta }/({\xi -\theta })$
, we have
![]() $\mathcal {L}_\psi (\mathcal {C}_L)\subset \mathcal {C}_{\xi L}$
and we have
$\mathcal {L}_\psi (\mathcal {C}_L)\subset \mathcal {C}_{\xi L}$
and we have
 $$ \begin{align*} \operatorname{\mathrm{diam}}_{\Theta_L}(\mathcal{L}_\psi(\mathcal{C}_L))\leq 2\log\bigg(\frac{1+\xi}{1-\xi}\bigg)+2\xi L. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{diam}}_{\Theta_L}(\mathcal{L}_\psi(\mathcal{C}_L))\leq 2\log\bigg(\frac{1+\xi}{1-\xi}\bigg)+2\xi L. \end{align*} $$
Proof. Let
![]() $\phi \in \mathcal {C}_L$
and let
$\phi \in \mathcal {C}_L$
and let
![]() $x,y\in \Sigma ^+$
be such that
$x,y\in \Sigma ^+$
be such that
![]() $d_\theta (x,y)\leq \theta $
. We obtain
$d_\theta (x,y)\leq \theta $
. We obtain
 $$ \begin{align*} \mathcal{L}_\psi\phi(x)&=\sum_{i=1}^ke^{\psi(ix)}\phi(ix)\leq e^{\theta(|\psi|_\theta+L)d_\theta(x,y)}\sum_{i=1}^ke^{\psi(iy)}\phi(iy)\\ &=e^{\theta(|\psi|_\theta+L)d_\theta(x,y)}\mathcal{L}_\psi\phi(y). \end{align*} $$
$$ \begin{align*} \mathcal{L}_\psi\phi(x)&=\sum_{i=1}^ke^{\psi(ix)}\phi(ix)\leq e^{\theta(|\psi|_\theta+L)d_\theta(x,y)}\sum_{i=1}^ke^{\psi(iy)}\phi(iy)\\ &=e^{\theta(|\psi|_\theta+L)d_\theta(x,y)}\mathcal{L}_\psi\phi(y). \end{align*} $$
The condition
![]() $\theta |\psi |_\theta +L\theta \leq \xi L$
holds if and only if
$\theta |\psi |_\theta +L\theta \leq \xi L$
holds if and only if
![]() $L\geq {\theta |\psi |_\theta }/({\xi -\theta })$
. Notice that
$L\geq {\theta |\psi |_\theta }/({\xi -\theta })$
. Notice that
![]() $\phi \in \mathcal {C}_L$
implies that there exists at least one cylinder set
$\phi \in \mathcal {C}_L$
implies that there exists at least one cylinder set
![]() $C_i=\{x\in \Sigma ^+ | x_0=i\}$
such that
$C_i=\{x\in \Sigma ^+ | x_0=i\}$
such that
![]() $\phi |_{C_i}>0$
. Thus,
$\phi |_{C_i}>0$
. Thus,
![]() $\mathcal {L}_\psi \phi (x)\geq e^{\psi (ix)}\phi (ix)>0$
. We may therefore apply Lemma A.3 to functions
$\mathcal {L}_\psi \phi (x)\geq e^{\psi (ix)}\phi (ix)>0$
. We may therefore apply Lemma A.3 to functions
![]() $\mathcal {L}_\psi \phi _1$
and
$\mathcal {L}_\psi \phi _1$
and
![]() $\mathcal {L}_\psi \phi _2$
:
$\mathcal {L}_\psi \phi _2$
:
 $$ \begin{align*}\Theta_L(\mathcal{L}_\psi\phi_1,\mathcal{L}_\psi\phi_2&\leq 2\log\bigg(\frac{1+\xi}{1-\xi}\bigg) + \log\sup_{x,y\in\Sigma^+}\bigg(\frac{\mathcal{L}_\psi\phi_1(x)\mathcal{L}_\psi\phi_2(y)}{\mathcal{L}_\psi\phi_1(y)\mathcal{L}_\psi\phi_2(x)} \bigg)\\&\leq 2\log\bigg(\frac{1+\xi}{1-\xi}\bigg)+\log(e^{2\xi L})= 2\log\bigg(\frac{1+\xi}{1-\xi}\bigg)+2\xi L.\\[-41pt] \end{align*} $$
$$ \begin{align*}\Theta_L(\mathcal{L}_\psi\phi_1,\mathcal{L}_\psi\phi_2&\leq 2\log\bigg(\frac{1+\xi}{1-\xi}\bigg) + \log\sup_{x,y\in\Sigma^+}\bigg(\frac{\mathcal{L}_\psi\phi_1(x)\mathcal{L}_\psi\phi_2(y)}{\mathcal{L}_\psi\phi_1(y)\mathcal{L}_\psi\phi_2(x)} \bigg)\\&\leq 2\log\bigg(\frac{1+\xi}{1-\xi}\bigg)+\log(e^{2\xi L})= 2\log\bigg(\frac{1+\xi}{1-\xi}\bigg)+2\xi L.\\[-41pt] \end{align*} $$
For
![]() $\phi \in \mathcal {F}^+$
, define the seminorm
$\phi \in \mathcal {F}^+$
, define the seminorm
 $$ \begin{align*} V(\phi):=\sup_{d_\theta(x,y)\leq\theta, x\neq y}\frac{|\phi(x)-\phi(y)|}{d_\theta(x,y)}, \end{align*} $$
$$ \begin{align*} V(\phi):=\sup_{d_\theta(x,y)\leq\theta, x\neq y}\frac{|\phi(x)-\phi(y)|}{d_\theta(x,y)}, \end{align*} $$
and set
![]() $\|\phi \|_L:=\max (\|\phi \|_\infty , ({1}/{2L})V(\phi ))$
. The next lemma gives the essential properties of the norm
$\|\phi \|_L:=\max (\|\phi \|_\infty , ({1}/{2L})V(\phi ))$
. The next lemma gives the essential properties of the norm
![]() $\|\cdot \|_L$
.
$\|\cdot \|_L$
.
Lemma A.5. The norm
![]() $\|\cdot \|_L$
is equivalent to
$\|\cdot \|_L$
is equivalent to
![]() $\|\cdot \|_\theta $
, and for all
$\|\cdot \|_\theta $
, and for all
![]() $\phi ,\psi \in \mathcal {F}^+$
, we have that
$\phi ,\psi \in \mathcal {F}^+$
, we have that
![]() $-\phi _2\leq _{\mathcal {C}_L}\phi _1\leq _{\mathcal {C}_L} \phi _2$
implies that
$-\phi _2\leq _{\mathcal {C}_L}\phi _1\leq _{\mathcal {C}_L} \phi _2$
implies that
![]() $\|\phi _1\|_L\leq \|\phi _2\|_L$
.
$\|\phi _1\|_L\leq \|\phi _2\|_L$
.
Proof. Given
![]() $\phi \in \mathcal {C}_L$
,
$\phi \in \mathcal {C}_L$
,
![]() $\varepsilon>0,$
and
$\varepsilon>0,$
and
![]() $x,y\in \Sigma ^+$
such that
$x,y\in \Sigma ^+$
such that
![]() $d_\theta (x,y)\leq \theta $
, we have
$d_\theta (x,y)\leq \theta $
, we have
 $$ \begin{align*} |\phi(x)-\phi(y)|=|e^{(\phi(x)+\varepsilon)}-e^{(\phi(y)+\varepsilon)}|\leq (\|\phi\|_\infty+\varepsilon)\bigg|\frac{\phi(x)+\varepsilon}{\phi(y)+\varepsilon}\bigg|\leq (\|\phi\|_\infty+\varepsilon)Ld_\theta(x,y). \end{align*} $$
$$ \begin{align*} |\phi(x)-\phi(y)|=|e^{(\phi(x)+\varepsilon)}-e^{(\phi(y)+\varepsilon)}|\leq (\|\phi\|_\infty+\varepsilon)\bigg|\frac{\phi(x)+\varepsilon}{\phi(y)+\varepsilon}\bigg|\leq (\|\phi\|_\infty+\varepsilon)Ld_\theta(x,y). \end{align*} $$
Letting
![]() $\varepsilon \rightarrow 0$
and taking the supremum, we get the estimate
$\varepsilon \rightarrow 0$
and taking the supremum, we get the estimate
![]() $V(\phi )\leq \|\phi \|_\infty $
. This gives us that
$V(\phi )\leq \|\phi \|_\infty $
. This gives us that
![]() $\|\phi \|_L\leq C\|\phi \|\theta $
for some
$\|\phi \|_L\leq C\|\phi \|\theta $
for some
![]() $C>0$
. Likewise, it is easy to see that
$C>0$
. Likewise, it is easy to see that
![]() $|\phi |_\theta \leq 2\|\phi \|_L$
, so we have that the norms are equivalent.
$|\phi |_\theta \leq 2\|\phi \|_L$
, so we have that the norms are equivalent.
Now suppose that
![]() $-\phi _2\leq _L\phi _1\leq _L\phi _2$
. Then,
$-\phi _2\leq _L\phi _1\leq _L\phi _2$
. Then,
![]() $\phi _2-\phi _1\geq 0$
and
$\phi _2-\phi _1\geq 0$
and
![]() $\phi _2+\phi _1\geq 0.$
In other words, for every
$\phi _2+\phi _1\geq 0.$
In other words, for every
![]() $x\in \Sigma ^+$
,
$x\in \Sigma ^+$
,
![]() $-\phi _2(x)\leq \phi _1(x)\leq \phi _2(x)$
, which implies that
$-\phi _2(x)\leq \phi _1(x)\leq \phi _2(x)$
, which implies that
![]() $\|\phi _1\|_\infty \leq \|\phi _2\|_\infty $
. To prove that
$\|\phi _1\|_\infty \leq \|\phi _2\|_\infty $
. To prove that
![]() $\|\phi _1\|_L\leq \|\phi _2\|_L$
, it suffices to prove that
$\|\phi _1\|_L\leq \|\phi _2\|_L$
, it suffices to prove that
![]() $V(\phi _1)\leq 2L\|\phi _2\|_\infty $
. We have
$V(\phi _1)\leq 2L\|\phi _2\|_\infty $
. We have
 $$ \begin{align*} V(\phi_1)&=V\bigg(\frac{\phi_1-\phi_2}{2}-\frac{\phi_1+\phi_2}{2}\bigg)\leq \frac{1}{2}(V(\phi_2-\phi_1)+V(\phi_2+\phi_1))\\&\leq \frac{L}{2}(\|\phi_2-\phi_1\|_\infty+\|\phi_2+\phi_1\|_\infty)\leq 2L\|\phi_2\|_\infty.\\[-43pt] \end{align*} $$
$$ \begin{align*} V(\phi_1)&=V\bigg(\frac{\phi_1-\phi_2}{2}-\frac{\phi_1+\phi_2}{2}\bigg)\leq \frac{1}{2}(V(\phi_2-\phi_1)+V(\phi_2+\phi_1))\\&\leq \frac{L}{2}(\|\phi_2-\phi_1\|_\infty+\|\phi_2+\phi_1\|_\infty)\leq 2L\|\phi_2\|_\infty.\\[-43pt] \end{align*} $$
Observe that for
![]() $\phi \in \mathcal {F}^+, \phi \geq 0$
, and
$\phi \in \mathcal {F}^+, \phi \geq 0$
, and
![]() $\alpha=|\phi|_\theta/L>0$
. we have for all
$\alpha=|\phi|_\theta/L>0$
. we have for all
![]() $x,y\in \Sigma ^+$
,
$x,y\in \Sigma ^+$
,
Hence,
![]() $\phi +\alpha \in \mathcal {C}_L$
.
$\phi +\alpha \in \mathcal {C}_L$
.
Proof of Lemma 3.1
Note that for every
![]() $f\in \mathcal {W}$
, if we take
$f\in \mathcal {W}$
, if we take
![]() $\theta>{1}/{\gamma }$
, we have
$\theta>{1}/{\gamma }$
, we have
![]() $|\pi _f|_\theta \leq 1$
. Thus, for uniformity in Lemma 3.3, we need to take
$|\pi _f|_\theta \leq 1$
. Thus, for uniformity in Lemma 3.3, we need to take
where
![]() $M:=\max \{|\log (f')|_{C^1}\mid f\in \mathcal {W}\}$
. Let
$M:=\max \{|\log (f')|_{C^1}\mid f\in \mathcal {W}\}$
. Let
![]() $h_f$
be such that
$h_f$
be such that
![]() $\mathcal {L}_{\psi _f}h_f=e^{P(\psi _f)}h_f$
, and let
$\mathcal {L}_{\psi _f}h_f=e^{P(\psi _f)}h_f$
, and let
![]() $\nu _f$
be the corresponding measure such that
$\nu _f$
be the corresponding measure such that
![]() $\mathcal {L}_{\psi _f}^*\nu _f= e^{P(\psi _f)}\nu _f.$
Note that for all
$\mathcal {L}_{\psi _f}^*\nu _f= e^{P(\psi _f)}\nu _f.$
Note that for all
![]() $f\in \mathcal {W}$
,
$f\in \mathcal {W}$
,
![]() $P(\psi _f)=0$
. It can be shown that
$P(\psi _f)=0$
. It can be shown that
![]() $h_f\in \mathcal {C}_L$
for L taken as above. Hence, for any
$h_f\in \mathcal {C}_L$
for L taken as above. Hence, for any
![]() $x,y\in \Sigma ^+$
, we have
$x,y\in \Sigma ^+$
, we have
 $$ \begin{align*} h_f(x)&=\mathcal{L}_{\psi_f}h_f(x)=\sum_{i=1}^ke^{\psi_f(ix)}h_f(ix)\\&\leq e^{\theta(L+|\psi_f|_\theta)d_\theta(x,y)}\sum_{i=1}^ke^{\psi_f(iy)}h_f(iy)\leq e^{\theta(L+M)d_\theta(x,y)}h_f(y), \end{align*} $$
$$ \begin{align*} h_f(x)&=\mathcal{L}_{\psi_f}h_f(x)=\sum_{i=1}^ke^{\psi_f(ix)}h_f(ix)\\&\leq e^{\theta(L+|\psi_f|_\theta)d_\theta(x,y)}\sum_{i=1}^ke^{\psi_f(iy)}h_f(iy)\leq e^{\theta(L+M)d_\theta(x,y)}h_f(y), \end{align*} $$
and hence
![]() $|\log (h_f)|_\theta \leq \theta (L+M)$
, and so
$|\log (h_f)|_\theta \leq \theta (L+M)$
, and so
![]() $|\overline {\psi }_f|_\theta \leq M+\theta (L+M)+L+M= (2+\theta )M+(1+\theta )L$
. Thus, for the normalized operators
$|\overline {\psi }_f|_\theta \leq M+\theta (L+M)+L+M= (2+\theta )M+(1+\theta )L$
. Thus, for the normalized operators
![]() $\mathcal {L}_{\overline {\psi }_f}$
, we take
$\mathcal {L}_{\overline {\psi }_f}$
, we take
Moreover, one can show that
![]() $-\phi \leq _{\mathcal {C}_L}\psi \leq _{\mathcal {C}_L} \phi $
implies that
$-\phi \leq _{\mathcal {C}_L}\psi \leq _{\mathcal {C}_L} \phi $
implies that
where
![]() $\mu _f$
is the equilibrium state corresponding to
$\mu _f$
is the equilibrium state corresponding to
![]() $\overline {\psi }_f$
.
$\overline {\psi }_f$
.
Observe that for every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
Therefore, we may apply Lemma A.2 with
![]() $\|\cdot \|_1=\|\cdot \|_{L^1}$
,
$\|\cdot \|_1=\|\cdot \|_{L^1}$
,
![]() $\|\cdot \|_2=\|\cdot \|_L$
,
$\|\cdot \|_2=\|\cdot \|_L$
,
![]() $\phi =\mathcal {L}^n_{\overline {\psi }_f}\phi $
, and
$\phi =\mathcal {L}^n_{\overline {\psi }_f}\phi $
, and
![]() $\psi =\int \phi \,d\mu _f=\mathcal {L}^n_{\overline {\psi }_f}(\int \phi \,d\mu _f)$
:
$\psi =\int \phi \,d\mu _f=\mathcal {L}^n_{\overline {\psi }_f}(\int \phi \,d\mu _f)$
:
 $$ \begin{align*} \bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi-\int\phi \,d\mu_f\bigg\|_L&\leq \Big(e^{\Theta_L(\mathcal{L}^n_{\overline{\psi}_f}\phi,\mathcal{L}^n_{\overline{\psi}_f}(\int\phi \,d\mu_f))}-1\Big)\bigg\|\int\phi \,d\mu_f\bigg\|_L\\&\leq \Big(e^{\Theta_L(\mathcal{L}^n_{\overline{\psi}_f}\phi,\mathcal{L}^n_{\overline{\psi}_f}(\int\phi \,d\mu_f))}-1\Big)\|\phi\|_L. \end{align*} $$
$$ \begin{align*} \bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi-\int\phi \,d\mu_f\bigg\|_L&\leq \Big(e^{\Theta_L(\mathcal{L}^n_{\overline{\psi}_f}\phi,\mathcal{L}^n_{\overline{\psi}_f}(\int\phi \,d\mu_f))}-1\Big)\bigg\|\int\phi \,d\mu_f\bigg\|_L\\&\leq \Big(e^{\Theta_L(\mathcal{L}^n_{\overline{\psi}_f}\phi,\mathcal{L}^n_{\overline{\psi}_f}(\int\phi \,d\mu_f))}-1\Big)\|\phi\|_L. \end{align*} $$
Let
![]() $\Delta =\operatorname {\mathrm {diam}}_{\Theta _L}(\mathcal {L}_{\overline {\psi }_f}(\mathcal {C}_L))$
, and observe that Birkhoff’s inequality implies that for
$\Delta =\operatorname {\mathrm {diam}}_{\Theta _L}(\mathcal {L}_{\overline {\psi }_f}(\mathcal {C}_L))$
, and observe that Birkhoff’s inequality implies that for
![]() $\phi \in \mathcal {C}_L$
,
$\phi \in \mathcal {C}_L$
,
 $$ \begin{align*} \Theta_L\bigg(\mathcal{L}^n_{\overline{\psi}_f}\phi,\mathcal{L}^n_{\overline{\psi}_f}\bigg(\int\phi \,d\mu_f\bigg)\bigg)\leq \bigg(\tanh\bigg(\frac{\Delta}{4}\bigg)\bigg)^{n-1}\Delta\leq \Delta\tau_{\mathcal{W}}^{n-1} \end{align*} $$
$$ \begin{align*} \Theta_L\bigg(\mathcal{L}^n_{\overline{\psi}_f}\phi,\mathcal{L}^n_{\overline{\psi}_f}\bigg(\int\phi \,d\mu_f\bigg)\bigg)\leq \bigg(\tanh\bigg(\frac{\Delta}{4}\bigg)\bigg)^{n-1}\Delta\leq \Delta\tau_{\mathcal{W}}^{n-1} \end{align*} $$
for uniform
![]() $\tau _{\mathcal {W}}$
. Therefore, for
$\tau _{\mathcal {W}}$
. Therefore, for
![]() $\phi \in \mathcal {C}_L$
, we have
$\phi \in \mathcal {C}_L$
, we have
 $$ \begin{align*} \bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi-\int\phi \,d\mu_f\bigg\|_L\leq \bigg(\sum_{j=1}^\infty\frac{(\Delta\tau_{\mathcal{W}}^{n-1})^j}{j!}\bigg)\|\phi\|_L=C_{\mathcal{W}}\tau_{\mathcal{W}}^n\|\phi\|_L, \end{align*} $$
$$ \begin{align*} \bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi-\int\phi \,d\mu_f\bigg\|_L\leq \bigg(\sum_{j=1}^\infty\frac{(\Delta\tau_{\mathcal{W}}^{n-1})^j}{j!}\bigg)\|\phi\|_L=C_{\mathcal{W}}\tau_{\mathcal{W}}^n\|\phi\|_L, \end{align*} $$
where
![]() $C_{\mathcal {W}}$
is uniform. Since the norms are equivalent, we may replace
$C_{\mathcal {W}}$
is uniform. Since the norms are equivalent, we may replace
![]() $\|\cdot \|_L$
by
$\|\cdot \|_L$
by
![]() $\|\cdot \|_\theta $
. It remains to extend this bound to all
$\|\cdot \|_\theta $
. It remains to extend this bound to all
![]() $\phi \in \mathcal {F}_\theta ^+$
. If
$\phi \in \mathcal {F}_\theta ^+$
. If
![]() $\phi \geq 0$
, then
$\phi \geq 0$
, then
![]() $\phi +{|\phi |_\theta }/{L}\in \mathcal {C}_L$
, so
$\phi +{|\phi |_\theta }/{L}\in \mathcal {C}_L$
, so
 $$ \begin{align*} \bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi-\int\phi \,d\mu_f\bigg\|_\theta&=\bigg\|\mathcal{L}^n_{\overline{\psi}_f}\bigg(\phi+\frac{|\phi|_\theta}{L}\bigg)-\int\bigg(\phi+\frac{|\phi|_\theta}{L}\bigg) \,d\mu_f\bigg\|_\theta\\&\leq C_{\mathcal{W}}\tau_{\mathcal{W}}^n\bigg(\|\phi\|_\theta+\frac{|\phi|_\theta}{L}\bigg)\leq C_{\mathcal{W}}\tau_{\mathcal{W}}^n\|\phi\|_\theta \end{align*} $$
$$ \begin{align*} \bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi-\int\phi \,d\mu_f\bigg\|_\theta&=\bigg\|\mathcal{L}^n_{\overline{\psi}_f}\bigg(\phi+\frac{|\phi|_\theta}{L}\bigg)-\int\bigg(\phi+\frac{|\phi|_\theta}{L}\bigg) \,d\mu_f\bigg\|_\theta\\&\leq C_{\mathcal{W}}\tau_{\mathcal{W}}^n\bigg(\|\phi\|_\theta+\frac{|\phi|_\theta}{L}\bigg)\leq C_{\mathcal{W}}\tau_{\mathcal{W}}^n\|\phi\|_\theta \end{align*} $$
for a different (but still uniform)
![]() $C_{\mathcal {W}}$
. For general real-valued
$C_{\mathcal {W}}$
. For general real-valued
![]() $\phi \in \mathcal {F}_\theta ^+$
, we decompose
$\phi \in \mathcal {F}_\theta ^+$
, we decompose
![]() $\phi $
as
$\phi $
as
![]() $\phi =\phi ^+-\phi ^-$
, where
$\phi =\phi ^+-\phi ^-$
, where
![]() $\phi ^+,\phi ^-\geq 0$
. Then,
$\phi ^+,\phi ^-\geq 0$
. Then,
 $$ \begin{align*} \bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi-\int\phi \,d\mu_f\bigg\|_\theta&\leq \bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi^+-\int\phi^+ \,d\mu_f\bigg\|_\theta+\bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi^-\int\phi^- \,d\mu_f\bigg\|_\theta\\&\leq C_{\mathcal{W}}\tau_{\mathcal{W}}^n(\|\phi^+\|_\theta+\|\phi^-\|_\theta)\leq 2C_{\mathcal{W}}\tau_{\mathcal{W}}^n\|\phi\|_\theta. \end{align*} $$
$$ \begin{align*} \bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi-\int\phi \,d\mu_f\bigg\|_\theta&\leq \bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi^+-\int\phi^+ \,d\mu_f\bigg\|_\theta+\bigg\|\mathcal{L}^n_{\overline{\psi}_f}\phi^-\int\phi^- \,d\mu_f\bigg\|_\theta\\&\leq C_{\mathcal{W}}\tau_{\mathcal{W}}^n(\|\phi^+\|_\theta+\|\phi^-\|_\theta)\leq 2C_{\mathcal{W}}\tau_{\mathcal{W}}^n\|\phi\|_\theta. \end{align*} $$
The case of complex-valued
![]() $\phi $
is handled similarly.
$\phi $
is handled similarly.