Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-11T01:07:43.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Foliated hyperbolicity and foliations with hyperbolic leaves

Published online by Cambridge University Press:  17 September 2018

CHRISTIAN BONATTI ,
XAVIER GÓMEZ-MONT  and
MATILDE MARTÍNEZ
CHRISTIAN BONATTI
Affiliation:
Institut de Mathématiques de Bourgogne, CNRS – Université de Bourgogne, Dijon, France email bonatti@u-bourgogne.fr
XAVIER GÓMEZ-MONT
Affiliation:
Centro de Investigación en Matemáticas (CIMAT), Guanajuato, Mexico email gmont@cimat.mx
MATILDE MARTÍNEZ
Affiliation:
Facultad de Ingeniería, Universidad de la República, Montevideo, Uruguay email matildem@fing.edu.uy
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a lamination in a compact space and a laminated vector field 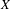$X$ which is hyperbolic when restricted to the leaves of the lamination, we distinguish a class of 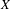$X$-invariant probabilities that describe the behavior of almost every 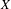$X$-orbit in every leaf, which we call Gibbs $u$-states. We apply this to the case of foliations in compact manifolds having leaves with negative curvature, using the foliated hyperbolic vector field on the unit tangent bundle to the foliation generating the leaf geodesics. When the Lyapunov exponents of such ergodic Gibbs $u$-states are negative, it is an SRB measure (having a positive Lebesgue basin of attraction). When the foliation is by hyperbolic leaves, this class of probabilities coincide with the classical harmonic measures introduced by Garnett. Furthermore, if the foliation is transversally conformal and does not admit a transverse invariant measure we show that there are finitely many ergodic Gibbs $u$-states, each supported in one minimal set of the foliation, each having negative Lyapunov exponents, and the union of their basins of attraction has full Lebesgue measure. The leaf geodesics emanating from a point have a proportion whose asymptotic statistics are described by each of these ergodic Gibbs $u$-states, giving rise to continuous visibility functions of the attractors. Reversing time, by considering 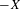$-X$, we obtain the existence of the same number of repellers of the foliated geodesic flow having the same harmonic measures as projections to 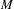$M$. In the case of only one attractor, we obtain a north to south pole dynamics.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 4 , April 2020 , pp. 881 - 903
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alvarez, S.. Harmonic measures and the foliated geodesic flow for foliations with negatively curved leaves. Ergod. Th. & Dynam. Sys. 36(2) (2016), 355–374.Google Scholar
Alvarez, S.. Gibbs u-states for the foliated geodesic flow and transverse invariant measures. Israel J. Math. 221(2) (2017), 869–940.Google Scholar
Alvarez, S.. Gibbs measures for foliated bundles with negatively curved leaves. Ergod. Th. & Dynam. Sys. 38(4) (2018), 1238–1288.Google Scholar
Alvarez, S. and Yang, J.. Physical measures for the geodesic flow tangent to a transversally conformal foliation. Ann. Inst. H. Poincaré Anal. Non Linéaire , doi:10.1016/j.anihpc.2018.03.009. Published online 9 April 2018.Google Scholar
Bakhtin, Y. and Martínez, M.. A characterization of harmonic measures on laminations by hyperbolic Riemann surfaces. Ann. Inst. Henri Poincaré Probab. Stat. 44(6) (2008), 1078–1089.Google Scholar
Bonatti, C., Díaz, L. J. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102). Mathematical Physics, III. Springer, Berlin, 2005.Google Scholar
Bonatti, C. and Gómez-Mont, X.. Sur le comportement statistique des feuilles de certains feuilletages holomorphes. Essays on Geometry and Related Topics, Vol. 1, 2 (Monographies de l’Enseignement Mathématique, 38). Enseignement Mathématique, Geneva, 2001, pp. 15–41.Google Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115 (2000), 157–193.Google Scholar
Brin, M. and Stuck, G.. Introduction to Dynamical Systems. Cambridge University Press, Cambridge, 2002.Google Scholar
Candel, A.. The harmonic measures of Lucy Garnett. Adv. Math. 176(2) (2003), 187–247.Google Scholar
Connell, C. and Martínez, M.. Harmonic and invariant measures on foliated spaces. Trans. Amer. Math. Soc. 369(7) (2017), 4931–4951.Google Scholar
Deroin, B. and Kleptsyn, V.. Random conformal dynamical systems. Geom. Funct. Anal. 17(4) (2007), 1043–1105.Google Scholar
Deroin, B. and Vernicos, C.. Feuilletage de Hirsch, mesures harmoniques et g-mesures. Publ. Mat. Urug. 12 (2011), 79–85.Google Scholar
Fathi, A., Herman, M.-R. and Yoccoz, J.-C.. A proof of Pesin’s stable manifold theorem. Geometric Dynamics (Rio de Janeiro, 1981) (Lecture Notes in Mathematics, 1007). Springer, Berlin, 1983, pp. 177–215.Google Scholar
Garnett, L.. Foliations, the ergodic theorem and Brownian motion. J. Funct. Anal. 51(3) (1983), 285–311.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54). Cambridge University Press, Cambridge, 1995. With a supplementary chapter by Katok and Leonardo Mendoza.Google Scholar
López-González, E.. Patterson–Sullivan-type measures on Riccati foliations with quasi-Fuchsian holonomy. Bull. Braz. Math. Soc. (N.S.) 44(3) (2013), 393–412.Google Scholar
Pesin, J. B.. Families of invariant manifolds that correspond to nonzero characteristic exponents. Izv. Akad. Nauk SSSR Ser. Mat. 40(6) (1976), 1332–1379, 1440.Google Scholar
Pugh, C. and Shub, M.. Ergodic attractors. Trans. Amer. Math. Soc. 312(1) (1989), 1–54.Google Scholar
Rokhlin, V. A.. On the fundamental ideas of measure theory. Trans. Amer. Math. Soc. 1(10) (1962), 1–52.Google Scholar
Shub, M.. Stabilité Globale des Systèmes Dynamiques (Astérisque, 56). Société Mathématique de France, Paris, 1978. With an English preface and summary.Google Scholar