Article contents
A generalization of the Jarník–Besicovitch theorem by continued fractions
Published online by Cambridge University Press: 11 February 2015
Abstract
We apply the tools of continued fractions to tackle the Diophantine approximation, including the classic Jarník–Besicovitch theorem, localized Jarník–Besicovitch theorem and its several generalizations. As is well known, the classic Jarník–Besicovitch sets, expressed in terms of continued fractions, can be written as 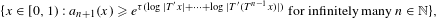 $$\begin{eqnarray}\{x\in [0,1):a_{n+1}(x)\geq e^{{\it\tau}(\log |T^{\prime }x|+\cdots +\log |T^{\prime }(T^{n-1}x)|)}~\text{for infinitely many}~n\in \mathbb{N}\},\end{eqnarray}$$
$$\begin{eqnarray}\{x\in [0,1):a_{n+1}(x)\geq e^{{\it\tau}(\log |T^{\prime }x|+\cdots +\log |T^{\prime }(T^{n-1}x)|)}~\text{for infinitely many}~n\in \mathbb{N}\},\end{eqnarray}$$ $T$ is the Gauss map and
$T$ is the Gauss map and 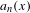 $a_{n}(x)$ is the
$a_{n}(x)$ is the  $n$th partial quotient of
$n$th partial quotient of  $x$. In this paper, we consider the size of the generalized Jarník–Besicovitch set
$x$. In this paper, we consider the size of the generalized Jarník–Besicovitch set 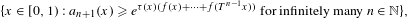 $$\begin{eqnarray}\{x\in [0,1):a_{n+1}(x)\geq e^{{\it\tau}(x)(f(x)+\cdots +f(T^{n-1}x))}~\text{for infinitely many}~n\in \mathbb{N}\},\end{eqnarray}$$
$$\begin{eqnarray}\{x\in [0,1):a_{n+1}(x)\geq e^{{\it\tau}(x)(f(x)+\cdots +f(T^{n-1}x))}~\text{for infinitely many}~n\in \mathbb{N}\},\end{eqnarray}$$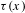 ${\it\tau}(x)$ and
${\it\tau}(x)$ and 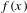 $f(x)$ are positive functions defined on
$f(x)$ are positive functions defined on 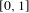 $[0,1]$.
$[0,1]$.
Information
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2015
References
- 11
- Cited by

