Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T17:26:41.947Z Has data issue: false hasContentIssue false
  • English
  • Français

Geodesic planes in geometrically finite acylindrical 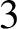$3$-manifolds

Part of: Lie groups Ergodic theory

Published online by Cambridge University Press:  04 May 2021

YVES BENOIST  and
HEE OH
YVES BENOIST*
Affiliation:
CNRS, Universite Paris-Sud, IMO, Batiment 307, 91405 Orsay, France
HEE OH
Affiliation:
Mathematics Department, Yale University, 10 Hillhouse Avenue, New Haven, CT06511, USA (e-mail: hee.oh@yale.edu)
*
e-mail: yves.benoist@u-psud.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let M be a geometrically finite acylindrical hyperbolic 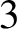$3$ -manifold and let 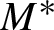$M^*$ denote the interior of the convex core of M. We show that any geodesic plane in 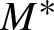$M^*$ is either closed or dense, and that there are only countably many closed geodesic planes in 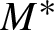$M^*$ . These results were obtained by McMullen, Mohammadi and Oh [Geodesic planes in hyperbolic 3-manifolds. Invent. Math.209 (2017), 425–461; Geodesic planes in the convex core of an acylindrical 3-manifold. Duke Math. J., to appear, Preprint, 2018, arXiv:1802.03853] when M is convex cocompact. As a corollary, we obtain that when M covers an arithmetic hyperbolic 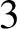$3$ -manifold 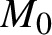$M_0$ , the topological behavior of a geodesic plane in 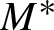$M^*$ is governed by that of the corresponding plane in 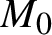$M_0$ . We construct a counterexample of this phenomenon when 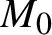$M_0$ is non-arithmetic.

Keywords

group actionshyperbolic 3-manifoldgeodesically finite groupstopological dynamics

MSC classification

Primary: 37A17: Homogeneous flows
Secondary: 22E40: Discrete subgroups of Lie groups
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 2: Anatole Katok Memorial Issue Part 1: Special Issue of Ergodic Theory and Dynamical Systems , February 2022 , pp. 514 - 553
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Anatole Katok who was so enthusiastic in sharing with us his encyclopedic knowledge and his deep insights in dynamical systems.

References

Abikoff, W.. On boundaries of Teichmüller spaces and on Kleinian groups III. Acta Math. 134 (1975), 221–237.CrossRefGoogle Scholar
Ahlfors, L.. The structure of a finitely generated Kleinian group. Acta Math. 122 (1969), 1–17.CrossRefGoogle Scholar
Ahlfors, L.. Complex Analysis. McGraw-Hill, New York, 1979.Google Scholar
Bader, U., Fisher, D., Miller, N. and Stover, M.. Arithmeticity, superrigidity, and totally geodesic submanifolds. JEMS, to appear, Preprint, arXiv:1903.08467.Google Scholar
Bishop, C.. On a theorem of Beardon and Maskit. Ann. Acad. Sci. Fenn. Math. 21 (1996), 383–388.Google Scholar
Borel, A.. Introduction aux groupes arithmétiques. Hermann, Paris, 1969.Google Scholar
Borel, A. and Tits, J.. Homomorphismes ‘abstraits’ de groupes algébriques simples. Ann. of Math. 97 (1973), 499–571.Google Scholar
Bowditch, B. H.. Geometrical finiteness for hyperbolic groups. J. Funct. Anal. 113 (1993), 245–317.CrossRefGoogle Scholar
Dal’bo, F.. Topologie du feuilletage fortement stable. Ann. Inst. Fourier 50 (2000), 981–993.CrossRefGoogle Scholar
Eberlein, P.. Geodesic flows on negatively curved manifolds, I. Ann. of Math. 95 (1972), 492–510.CrossRefGoogle Scholar
Fisher, D., Lafont, J. F., Miller, N. and Stover, M.. Finiteness of maximal geodesic submanifolds in hyperbolic hybrids. Preprint, 2018, arXiv:1802.04619.Google Scholar
Floyd, W. J.. Group completions and limit sets of Kleinian groups. Invent. Math. 57 (1980), 205–218.Google Scholar
Gromov, M. and Piatetski-Shapiro, I.. Non-arithmetic groups in Lobachevsky spaces. Publ. Math. Inst. Hautes Études Sci. 66 (1988), 93–103.CrossRefGoogle Scholar
Hatcher, A.. Algebraic Topology. Cambridge University Press, Cambridge, 2002.Google Scholar
Khalil, O.. Geodesic planes in geometrically finite manifolds. Discrete Contin. Dyn. Syst. 39 (2019), 881–903.CrossRefGoogle Scholar
Lee, M. and Oh, H.. Orbit closures of unipotent flows for hyperbolic manifolds with Fuchsian ends. Preprint, 2019, arXiv:1902.06621.Google Scholar
Lehto, O. and Virtanen, K. J.. Quasiconformal Mappings in the Plane. Springer, Berlin, 1973.CrossRefGoogle Scholar
Maclachlan, C. and Reid, A.. The Arithmetic of Hyperbolic 3-Manifolds (Graduate Texts in Mathematics, 219). Springer, New York, 2003.CrossRefGoogle Scholar
Marden, A.. Outer Circles. Cambridge University Press, Cambridge, 2007.CrossRefGoogle Scholar
Margulis, G.. Indefinite quadratic forms and unipotent flows on homogeneous spaces. Banach Center Publ. 23 (1989), 399–409.CrossRefGoogle Scholar
Margulis, G. and Mohammadi, A.. Arithmeticity of hyperbolic 3-manifolds containing infinitely many totally geodesic surfaces. Preprint, 2019, arXiv:1902.07267.Google Scholar
Maskit, B.. On boundaries of Teichmuller spaces and on Kleinian groups II. Ann. of Math. 91 (1970), 607–639.CrossRefGoogle Scholar
Maskit, B.. Intersections of component subgroups of Kleinian groups. Ann. of Math. Stud. 79 (1974), 349–367.Google Scholar
Matsuzaki, K. and Taniguchi, M., Hyperbolic Manifolds and Kleinian Groups . Oxford University Press, Oxford, 1998.Google Scholar
McMullen, C.. Iteration on Teichmuller space. Invent. Math. 99 (1990), 425–454.CrossRefGoogle Scholar
McMullen, C., Mohammadi, A. and Oh, H.. Geodesic planes in hyperbolic $3$ -manifolds. Invent. Math. 209 (2017), 425–461.CrossRefGoogle Scholar
McMullen, C., Mohammadi, A. and Oh, H.. Geodesic planes in the convex core of an acylindrical $3$ -manifold. Duke Math. J., to appear, Preprint, 2018, arXiv:1802.03853.Google Scholar
Oh, H.. Dynamics for discrete subgroups of ${SL}_2(\mathbb{C}).$ Margulis vol., to appear, Preprint, 2019, arXiv:1909.02922.Google Scholar
Oh, H. and Shah, N.. Equidistribution and Counting for orbits of geometrically finite hyperbolic groups. J. Amer. Math. Soc. 26 (2013), 511–562.CrossRefGoogle Scholar
Ratner, M.. Raghunathan’s topological conjecture and distributions of unipotent flows. Duke Math. J. 63 (1991), 235–280.CrossRefGoogle Scholar
Serre, J. P.. Cours d’arithmétique (Graduate Texts in Mathematics, 7). Springer, New York, 1973.Google Scholar
Shah, N.. Closures of totally geodesic immersions in manifolds of constant negative curvature. Group Theory from a Geometrical Viewpoint. World Scientific Publishing, Singapore, 1991, pp. 718–732.Google Scholar
Thurston, W. P.. Hyperbolic geometry and 3-manifolds. Low Dimensional Topology (London Mathematical Society Lecture Note Series, 48). Cambridge University Press, Cambridge, 1982, pp. 9–25.CrossRefGoogle Scholar
Thurston, W. P.. Hyperbolic structures on $3$ -manifolds I: deformation of acylindrical manifolds. Ann. of Math. 124 (1986), 203–246.CrossRefGoogle Scholar
Waldhausen, F.. On irreducible $3$ -manifolds which are sufficiently large. Ann. of Math. 87 (1968), 56–88.CrossRefGoogle Scholar
Zhang, Y.. Construction of acylindrical hyperbolic 3-manifolds with quasifuchsian boundary. Exp. Math., to appear.Google Scholar
Zhang, Y.. Existence of an exotic plane in an acylindrical 3-manifold. Preprint, 2020.Google Scholar
Zimmer, R.. Ergodic Theory and Semisimple Groups. Birkhauser, Basel, 1984.CrossRefGoogle Scholar