Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Hui
2016.
Purely infinite totally disconnected topological graph algebras.
Illinois Journal of Mathematics,
Vol. 60,
Issue. 3-4,
Carlsen, Toke
Ruiz, Efren
and
Sims, Aidan
2016.
Equivalence and stable isomorphism of groupoids, and diagonal-preserving stable isomorphisms of graph 𝐶*-algebras and Leavitt path algebras.
Proceedings of the American Mathematical Society,
Vol. 145,
Issue. 4,
p.
1581.
Li, Xin
2016.
Partial Transformation Groupoids Attached to Graphs and Semigroups.
International Mathematics Research Notices,
p.
rnw166.
Chung, Nhan-Phu
and
Jiang, Yongle
2017.
Continuous cocycle superrigidity for shifts and groups with one end.
Mathematische Annalen,
Vol. 368,
Issue. 3-4,
p.
1109.
Carlsen, Toke Meier
and
Rout, James
2017.
Diagonal-preserving gauge-invariant isomorphisms of graph C⁎-algebras.
Journal of Functional Analysis,
Vol. 273,
Issue. 9,
p.
2981.
Brown, Jonathan H.
Clark, Lisa Orloff
and
an Huef, Astrid
2017.
Diagonal-preserving ring ⁎-isomorphisms of Leavitt path algebras.
Journal of Pure and Applied Algebra,
Vol. 221,
Issue. 10,
p.
2458.
Ara, Pere
Bosa, Joan
Hazrat, Roozbeh
and
Sims, Aidan
2017.
Reconstruction of graded groupoids from graded Steinberg algebras.
Forum Mathematicum,
Vol. 29,
Issue. 5,
p.
1023.
Carlsen, Toke Meier
2018.
⁎-isomorphism of Leavitt path algebras over Z.
Advances in Mathematics,
Vol. 324,
Issue. ,
p.
326.
Hazrat, Roozbeh
and
Li, Huanhuan
2018.
Graded Steinberg algebras and partial actions.
Journal of Pure and Applied Algebra,
Vol. 222,
Issue. 12,
p.
3946.
Carlsen, Toke Meier
and
Rout, James
2018.
Diagonal-preserving graded isomorphisms of Steinberg algebras.
Communications in Contemporary Mathematics,
Vol. 20,
Issue. 06,
p.
1750064.
Matsumoto, Kengo
2018.
Relative Morita equivalence of Cuntz–Krieger algebras and flow equivalence of topological Markov shifts.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 10,
p.
7011.
ARKLINT, SARA E.
EILERS, SØREN
and
RUIZ, EFREN
2018.
A dynamical characterization of diagonal-preserving -isomorphisms of graph -algebras.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 7,
p.
2401.
Eilers, Søren
Restorff, Gunnar
Ruiz, Efren
and
Sørensen, Adam P.W.
2018.
Geometric Classification of Graph C*-algebras over Finite Graphs.
Canadian Journal of Mathematics,
Vol. 70,
Issue. 2,
p.
294.
Matsumoto, Kengo
2019.
State splitting, strong shift equivalence and stable isomorphism of Cuntz–Krieger algebras.
Dynamical Systems,
Vol. 34,
Issue. 1,
p.
93.
Gonçalves, Daniel
and
Royer, Danilo
2019.
Infinite Alphabet Edge Shift Spaces via Ultragraphs and Their C*-Algebras.
International Mathematics Research Notices,
Vol. 2019,
Issue. 7,
p.
2177.
Sims, Aidan
2019.
The suspension of a graph, and associated C⁎-algebras.
Journal of Functional Analysis,
Vol. 277,
Issue. 4,
p.
1202.
Carlsen, Toke Meier
Eilers, Søren
Ortega, Eduard
and
Restorff, Gunnar
2019.
Flow equivalence and orbit equivalence for shifts of finite type and isomorphism of their groupoids.
Journal of Mathematical Analysis and Applications,
Vol. 469,
Issue. 2,
p.
1088.
Yi, Inhyeop
2019.
Continuous Orbit Equivalence on Self-Similar Graph Actions.
Mathematics,
Vol. 7,
Issue. 10,
p.
990.
Nyland, Petter
and
Ortega, Eduard
2019.
Topological full groups of ample groupoids with applications to graph algebras.
International Journal of Mathematics,
Vol. 30,
Issue. 04,
p.
1950018.
Cordeiro, Luiz Gustavo
and
Beuter, Viviane
2020.
The dynamics of partial inverse semigroup actions.
Journal of Pure and Applied Algebra,
Vol. 224,
Issue. 3,
p.
917.
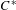 $C^{\ast }$ -algebras. We show that it is necessary to assume that every cycle has an exit for the forward implication, but that the reverse implication holds for arbitrary graphs. As part of our analysis of arbitrary graphs
$C^{\ast }$ -algebras. We show that it is necessary to assume that every cycle has an exit for the forward implication, but that the reverse implication holds for arbitrary graphs. As part of our analysis of arbitrary graphs 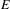 $E$ we construct a groupoid
$E$ we construct a groupoid 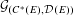 ${\mathcal{G}}_{(C^{\ast }(E),{\mathcal{D}}(E))}$ from the graph algebra
${\mathcal{G}}_{(C^{\ast }(E),{\mathcal{D}}(E))}$ from the graph algebra 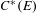 $C^{\ast }(E)$ and its diagonal subalgebra
$C^{\ast }(E)$ and its diagonal subalgebra 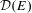 ${\mathcal{D}}(E)$ which generalises Renault’s Weyl groupoid construction applied to
${\mathcal{D}}(E)$ which generalises Renault’s Weyl groupoid construction applied to 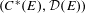 $(C^{\ast }(E),{\mathcal{D}}(E))$ . We show that
$(C^{\ast }(E),{\mathcal{D}}(E))$ . We show that 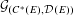 ${\mathcal{G}}_{(C^{\ast }(E),{\mathcal{D}}(E))}$ recovers the graph groupoid
${\mathcal{G}}_{(C^{\ast }(E),{\mathcal{D}}(E))}$ recovers the graph groupoid 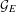 ${\mathcal{G}}_{E}$ without the assumption that every cycle in
${\mathcal{G}}_{E}$ without the assumption that every cycle in 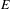 $E$ has an exit, which is required to apply Renault’s results to
$E$ has an exit, which is required to apply Renault’s results to 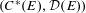 $(C^{\ast }(E),{\mathcal{D}}(E))$ . We finish with applications of our results to out-splittings of graphs and to amplified graphs.
$(C^{\ast }(E),{\mathcal{D}}(E))$ . We finish with applications of our results to out-splittings of graphs and to amplified graphs.
