Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kaliszewski, S.
and
Quigg, John
2013.
Coactions and Skew Products of Topological Graphs.
Integral Equations and Operator Theory,
Vol. 75,
Issue. 2,
p.
187.
Kaliszewski, S.
Quigg, John
and
Robertson, David
2013.
Functoriality of Cuntz–Pimsner correspondence maps.
Journal of Mathematical Analysis and Applications,
Vol. 405,
Issue. 1,
p.
1.
Bédos, Erik
Kaliszewski, S.
Quigg, John
and
Robertson, David
2015.
A new look at crossed product correspondences and associated C⁎-algebras.
Journal of Mathematical Analysis and Applications,
Vol. 426,
Issue. 2,
p.
1080.
Katsoulis, Elias George
2016.
C* Envelopes and the Hao-Ng Isomorphism for Discrete Groups.
International Mathematics Research Notices,
p.
rnw187.
Kaliszewski, S.
Landstad, Magnus
and
Quigg, John
2018.
Coaction functors, II.
Pacific Journal of Mathematics,
Vol. 293,
Issue. 2,
p.
301.
Katsoulis, Elias
2020.
Product systems of C*-correspondences and Takai duality.
Israel Journal of Mathematics,
Vol. 240,
Issue. 1,
p.
223.
Katsoulis, Elias G
and
Ramsey, Christopher
2021.
The Non-selfadjoint Approach to the Hao–Ng Isomorphism.
International Mathematics Research Notices,
Vol. 2021,
Issue. 2,
p.
1160.
Yaremenko, Mykola
2023.
The Dynamical Systems (A, G, ω) and Pseudo-differential Operators on Locally Compact Commutative Groups.
EQUATIONS,
Vol. 3,
Issue. ,
p.
59.
Yaremenko, Mykola
2023.
Twisted Dynamical Systems, Schrodinger Representations.
PROOF,
Vol. 3,
Issue. ,
p.
14.
Hall, Lucas
2024.
Coactions and skew products for topological quivers.
Proceedings of the Edinburgh Mathematical Society,
Vol. 67,
Issue. 3,
p.
921.

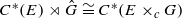 . We also define the fundamental group and the universal covering of a topological graph.
. We also define the fundamental group and the universal covering of a topological graph.