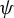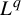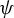Hölder continuity of measures for heavy tail potentials

Abstract

For a class of potentials $\psi $ satisfying a condition depending on the roof function of a suspension (semi)flow, we show an EKP inequality, which can be interpreted as a Hölder continuity property in the weak${^*}$ norm of measures, with respect to the pressure of those measures, where the Hölder exponent depends on the $L^q$-space to which $\psi $ belongs. This also captures a new type of phase transition for intermittent (semi)flows (and maps).

1 Introduction

There exist a wide range of dynamical systems having a unique measure of maximal entropy. That is, there exists a unique measure $\mu _0$ satisfying $h(\mu _0)= \sup \{h(\mu ) : {\mu \in \mathcal {M}}\}$ , where $h(\mu )$ denotes the entropy of the measure $\mu $ and $\mathcal {M}$ the space of invariant probability measures. If the phase space is compact and the entropy map is upper semi-continuous (with respect to the weak ${^*}$ topology), if $(\mu _n)_n$ is a sequence in $\mathcal {M}$ such that $\lim _{n \to \infty } h(\mu _n)=h(\mu _0)$ , then $(\mu _n)_n$ converges to $\mu _0$ . In particular, for any Lipschitz function $\psi $ , we have $\int \psi \, d \mu _n \rightarrow \int \psi \, d \mu _0$ . Polo [P, Theorem 4.1.1] made this statement effective for hyperbolic automorphisms of the tori and its corresponding measure of maximal entropy $\mu _0$ (the Haar measure in the case of linear automorphism). Indeed, he proved that there exists a constant $C>0$ such that for any invariant probability measure $\mu $ and any Lipschitz function $\psi $ , with Lipschitz constant L,

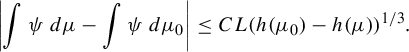(1.1) $$ \begin{align} \bigg| \kern-3pt\int \psi \, d \mu - \int \psi \, d \mu_0 \bigg| \leq CL (h(\mu_0)-h(\mu) )^{1/3}. \end{align} $$

This result can be thought of as a Hölder continuity property in the weak ${^*}$ norm of measures. According to Polo [P, p. 6], it was Einsiedler who outlined the argument for the proof of equation (1.1) in the case of a $\times 2$ map. Kadyrov [K, Theorem 1.1] later extended this result to sub-shifts of finite type (defined over finite alphabets). In his case, instead of a cubic root, he had a quadratic root. Inequalities such as equation (1.1) are now called EKP inequalities after these authors. The case of countable Markov shifts has been studied recently. In that setting, the phase space is no longer compact and the entropy map is not always upper semi-continuous. Moreover, there are cases in which there is no measure of maximal entropy. Therefore, further assumptions are required for EKP inequalities to make sense. For example, Rühr [R, Theorem 1.1] studied countable Markov shifts satisfying a combinatorial assumption (the BIP property). This class of systems shares many properties with sub-shifts of finite type. However, they have infinite entropy, thus EKP inequalities do not make sense for the measures of maximal entropy. Instead, he considered the Gibbs measure associated to a locally Hölder function of finite pressure. In that setting, the right-hand side of the EKP inequality has the free energy of the measures (instead of the entropy) and a square root. Since systems having the BIP property are similar to sub-shifts of finite type, the arguments in the proof are close to those developed by Kadyrov.

Sarig and Rühr recently studied finite entropy countable Markov shifts. In this case, instead of making a strong assumption on the system, they consider strongly positive recurrent (SPR) functions. Potentials in this class have unique equilibrium measures and the corresponding transfer operator acts with a spectral gap in appropriate Banach spaces [CS, Theorem 2.1]. They proved [RS, Theorem 6.1] that if $\phi $ is an SPR regular function, $\mu _{\phi }$ is the associated equilibrium measure and $\psi $ a regular function, then for any invariant measure $\mu $ with sufficiently large free energy $P_{\mu }(\phi )$ (see §2.1), we have

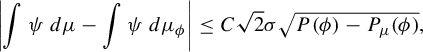(1.2) $$ \begin{align} \bigg| \kern-3pt\int \psi \, d \mu - \int \psi \, d \mu_\phi \bigg| \leq C\sqrt2 \sigma \sqrt{P(\phi)- P_{\mu}(\phi)}, \end{align} $$

where $P(\phi )$ is the pressure of $\phi $ and $\sigma ^2$ is the asymptotic variance of $\psi $ with respect to $\mu _\phi $ (which in turn is related to the second derivative of the pressure function) and C is a constant which can be taken close to 1 provided $| \kern -3pt\int \psi \, d \mu - \int \psi \, d \mu _\phi |$ is small. They also provide a version where the integrals can be far apart and where $C \sigma $ is replaced by $C'\|\psi \|_\beta $ for a suitable norm, where $C'$ is independent of $\psi $ .

In this article, we prove EKP inequalities for continuous time dynamical systems which may not be SPR and can have unbounded entropy, for some unbounded $\psi $ . Indeed, we study suspension (semi)flows over Gibbs–Markov maps $T:Y\to Y$ and unbounded roof function $\tau :Y\to (0, \infty )$ with $\inf \tau>0$ satisfying certain additional assumptions. Our main focus is towards systems with weak hyperbolicity properties. We denote the (semi)flow by $(F_t)_t$ and the suspension space by $Y^{\tau }$ . We refer to §2 for details. Consider a regular potential $\phi $ and its corresponding positive entropy equilibrium state $\nu _{\phi }$ . In our main results, we establish several EKP inequalities for $\nu _{\phi }$ , for a regular function $\psi $ and for invariant measures $\nu $ satisfying $\int \psi \, d \nu> \int \psi \, d \nu _{\phi }$ . We bound the difference $\int \psi \, d \nu - \int \psi \, d \nu _{\phi }$ with terms of the form $(P(\phi ) - P_{\nu }(\phi ))^{\rho }$ . The values of $\rho $ are related to dynamical properties of the system.

To be more precise, we have two basic assumptions. The first, assumption (GM0), describes the decay of the tail of the measure on the base map T. It essentially says that there exists $\beta>1$ such that $\mu (\tau>x) \leq cx^{-\beta }$ . To state our second, assumption (GM1), recall that every potential $\psi $ for the (semi)flow has an induced version $\bar \psi $ defined on Y. The assumptions of our results are in terms of the induced potentials. It states that ${\bar \psi = C_0 -\psi _0}$ , where $0 \leq \psi _0 \leq C_1 \tau ^{\gamma }$ and $\gamma \in (\beta -1, \beta )$ . We stress that these assumptions are fulfilled by a wide range of functions $\psi $ .

In our first result, Theorem 2.8, we assume that $\beta / \gamma>3$ . We show that there exists $\epsilon>0$ such that for any flow invariant probability measure $\nu $ , with $\int \psi ~d\nu \in (\int \psi ~d\nu _\phi , \int \psi ~d\nu _\phi +{\epsilon })$ , we have

$$ \begin{align*} \int\psi\,d\nu-\int\psi\,d\nu_{\phi} \le C_{\phi, \psi} {\sqrt 2}\sigma\sqrt{P_{\nu_\phi}(\phi)-P_\nu(\phi)}, \end{align*} $$

where $\sigma ^2$ is the asymptotic variance of $\psi $ with respect to $\nu _{\phi }$ and where $C_{\phi , \psi } \geq 1$ tends to $1$ as $\int \psi \, d\nu \to \int \psi \, d\nu _{\phi }$ .

We note that in the expression above, as well as those in items (a) and (b) below, are only useful when $\int \psi \,d\nu>\int \psi \,d\nu _{\phi }$ . It can be shown in the main examples of this theory that this is intrinsically necessary (though if $\mu (\tau>x)$ decays exponentially, then the proofs can be rewritten to recover a statement like equation (1.2)), rather than an artefact of the proof, that is, we cannot put absolute value signs on the left-hand side of these equations and allow $\int \psi \,d\nu <\int \psi \,d\nu _{\phi }$ , see Remark 2.13.

In our second main result, Theorem 2.9, we consider the cases in which $\beta / \gamma \in (1,2]$ and $\beta / \gamma \in (2,3)$ (with some additional assumptions). This result captures a new type of phase transition. Indeed, while item (b) below shows an EKP inequality in the case $\beta /\gamma \in (2,3)$ (when the central limit theorem (CLT) is present), item (a) gives a new type of EKP inequality with the exponent changing from $1/2$ to one depending on the ratio $\beta /\gamma $ . Interestingly, this result captures the transition form stable law to CLT in terms of the Hölder continuity of the pressure (see Remark 2.11).

1. (a) If $\beta /\gamma \in (1,2]$ , then

   $$ \begin{align*} \int\psi\,d\nu-\int\psi\,d\nu_{\phi}\le c_2 (P_{\nu_\phi}(\phi)-P_\nu(\phi))^{({\beta-\gamma})/({\beta-\gamma+1})}. \end{align*} $$

2. (b) If $\beta /\gamma \in (2,3)$ , then

   $$ \begin{align*} \int\psi\,d\nu-\int\psi\,d\nu_{\phi}\le c_3 {\sqrt 2}\sigma\sqrt{P_{\nu_\phi}(\phi)-P_\nu(\phi)}. \end{align*} $$

The above results give the most interesting behaviour and best constants, when $ \int \psi \,d\nu $ and $\int \psi \,d\nu _{\phi }$ are close to each other, but we also give a result Theorem 2.14 similar to the above when these integrals are far away from each other.

The proof of our results is based on asymptotic estimates of the pressure function ${s \mapsto P_F(\phi + s\psi )}$ . For example, in Proposition 2.4, we prove, under the assumptions (GM0) and (GM1), that if $q_1 \in [1, \beta / \gamma ]$ , then $P_F(\phi + s\psi )$ is of class $C^{q_1}$ . In Proposition 2.6, under assumption (GM0) and an assumption on the decay of the tail of the measure, we establish estimates of the type: if $\beta /\gamma \in (1,2]$ , then $ P_F"(\phi + s\psi )=C s^{\beta -\gamma -1}(1+o(1))$ . Moreover, if $\beta /\gamma \in (2, 3)$ , then $P_F"(\phi + s\psi )=-C s^{\beta -2\gamma -1}(1+o(1))$ . These estimates are essential in the proofs of the main results and are obtained building up from [BTT1, BTT2, MT]. With these in hand, we make use of the restricted pressure in a similar way to [RS].

In §7, examples of dynamical systems for which the results obtained in the article apply are provided. We construct suspension flows over maps exhibiting weak forms of hyperbolicity. Indeed, the class of interval maps we consider have parabolic fixed points. This shows the strength of our main results.

2 Suspension flows over Gibbs–Markov (GM) maps with unbounded roof $\tau $

2.1 Thermodynamic formalism for suspension flows

Let $T:Y\to Y$ be a map and ${\tau :Y\to (0, \infty )}$ a positive function with $\inf \tau>0$ . Consider the space $Y^\tau =Y\times [0, \infty )/\sim $ where $(y, \tau (y))\sim (T(y), 0)$ . The suspension (semi)flow over T with roof function $\tau $ is the (semi)flow $(F_t)_t$ defined by $F_{t'}(y, t) = (y, t+t')$ for $t'\in [0,\tau (y))$ .

Denote by $\mathcal {M}_{F}$ and respectively $\mathcal {M}_T$ the spaces of F-invariant and $T-$ invariant probability measures. There is a close relation between these spaces. Indeed, consider the subset of $\mathcal {M}_T$ for which $\tau $ is integrable. That is,

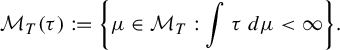(2.1) $$ \begin{align} \mathcal{M}_T(\tau):= \bigg\{ \mu \in \mathcal{M}_{T}: \int \tau \, d \mu < \infty \bigg\}. \end{align} $$

Let m denote the one-dimensional Lebesgue measure and $\mu \in \mathcal {M}_T(\tau )$ . It follows directly from classical results by Ambrose and Kakutani [AK] that

(2.2) $$ \begin{align} \nu= \frac{(\mu \times m)|_{Y^\tau} }{(\mu \times m)(Y^\tau)} = \frac{(\mu \times m)|_{Y^\tau} }{\int\tau~d\mu} \in \mathcal{M}_{F}. \end{align} $$

Actually, under the assumption that $\inf \tau>0$ , equation (2.2) establishes a one-to-one correspondence between measures in $\mathcal {M}_F$ and measures in $\mathcal {M}_T(\tau )$ . We say that $\mu $ is the lift of $\nu $ and that $\nu $ is the projection of $\mu $ . In the setting of this article, every measure in $\mathcal {M}_F$ lifts to some measure in $\mathcal {M}_T$ .

The entropies of measures as in equation (2.2) are related. Indeed, for $\mu \in \mathcal {M}_T$ and $\nu \in \mathcal {M}_F$ , denote by $h_T(\mu )$ and $h_F(\nu )$ the corresponding entropies. Abramov [Ab] proved that $h_F(\nu ) = {h_T(\mu )}/{\int \tau \, d\mu }$ .

It is also possible to relate the integral of a function on the flow to a corresponding one on the base. For $\phi :Y^{\tau } \to \mathbb {R}$ , we define its induced version $\bar \phi (x):Y \to \mathbb {R}$ by $\bar \phi (x) = \int _0^{\tau (x)} \phi \circ F_t(x, 0)\, dt$ . Let $\mu \in \mathcal {M}_T$ and $\nu \in \mathcal {M}_F$ be related as in equation (2.2). Kac’s formula establishes the following relation: $\int \phi \, d\nu = {\int \bar \phi \, d\mu }/{\int \tau \,d\mu }$ .

Having related the spaces of invariant measures, the corresponding entropies and integrals, it should come as no surprise that thermodynamic formalism on the flow is related to that on the base. Given a regular function $\phi :Y^{\tau } \to \mathbb {R}$ , we define the pressure of $\phi $ (with respect to the (semi)flow F) by

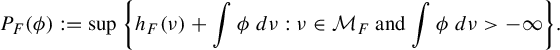$$ \begin{align*} P_F(\phi) := \sup\bigg\{h_F(\nu)+ \int\phi~d\nu: \nu\in \mathcal{M}_F \ \textrm{and} \int\phi~d\nu>-\infty \bigg\}. \end{align*} $$

It will be convenient to write $P_{F, \nu }(\phi ) = h_F(\nu )+ \int \phi ~d\nu $ for $\nu \in \mathcal {M}_F$ , when this sum makes sense. We call $\nu \in \mathcal {M}_F$ an equilibrium state for $\phi $ if $P_{F, \nu }(\phi )= P_F(\phi )$ and write $\nu =\nu _\phi $ . Similarly, the pressure of $\bar \phi : Y \to \mathbb {R}$ (with respect to the map T) is defined by

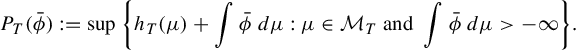$$ \begin{align*} P_T(\bar\phi) := \sup\bigg\{h_T(\mu)+ \int\bar\phi~d\mu: \mu\in \mathcal{M}_T \text{ and } \int\bar\phi~d\mu>-\infty \bigg\}. \end{align*} $$

Again, it will be convenient to write $P_{T,\mu }(\bar \phi ) = h_T(\mu )+ \int \bar \phi ~d\mu $ for $\mu \in \mathcal {M}_T$ , when this sum makes sense. We call $\mu \in \mathcal {M}_T$ an equilibrium state for $\bar \phi $ if $P_{T, \mu }(\bar \phi )= P_T(\bar \phi )$ and write $\mu =\mu _{\bar \phi }$ .

Remark 2.1. Note that, under the assumptions we have considered here, Abramov’s and Kac’s formulae imply that

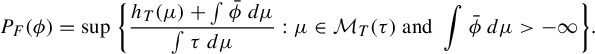$$ \begin{align*} P_F(\phi)=\sup\bigg\{\frac{h_T(\mu)+ \int\bar\phi~d\mu}{\int\tau~d\mu}: \mu\in \mathcal{M}_T(\tau) \text{ and } \int\bar\phi~d\mu>-\infty \bigg\}. \end{align*} $$

We will assume that $P_F(\phi )=0$ (otherwise, we can shift the potential by a constant). This implies that $P_T(\bar \phi )\le 0$ . Moreover, in this paper, liftability of all measures implies in fact that $P_T(\bar \phi )=0$ . Under an integrability condition, equilibrium states for $\phi $ and $\bar \phi $ are also related. Indeed, if $\mu _{\bar \phi }\in \mathcal {M}_T(\tau )$ , then the equilibrium state for $\phi $ is

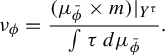$$ \begin{align*} \nu_\phi= \frac{(\mu_{\bar\phi} \times m)|_{Y^\tau} }{\int\tau~d\mu_{\bar\phi}}. \end{align*} $$

We conclude this section with the following definition, which is analogous to [RS, Definition 3.1]:

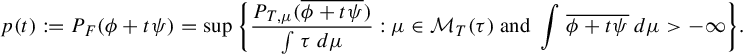$$ \begin{align*} p(t) := P_F(\phi+t\psi) = \sup\bigg\{\frac{P_{T, \mu}(\overline{\phi+t\psi})}{\int\tau~d\mu}:\mu\in \mathcal{M}_T(\tau) \text{ and } \int\overline{\phi+t\psi}~d\mu>-\infty\bigg\}. \end{align*} $$

2.2 Gibbs–Markov maps and the main assumptions

Roughly speaking, Gibbs–Markov maps are infinite branch uniformly expanding maps with bounded distortion and big images. We recall the definitions in more detail. Let $(Y,\mu _Y)$ be a probability space and let $T:Y\to Y$ be a topologically mixing ergodic measure-preserving transformation, piecewise continuous with respect to a non-trivial countable partition $\{a\}$ . Define $s(y,y')$ to be the least integer $n\ge 0$ such that $T^ny$ and $T^ny'$ lie in distinct partition elements. Assuming that $s(y,y')=\infty $ if and only if $y=y'$ , one obtains that $d_\theta (y,y')=\theta ^{s(y,y')}$ for $\theta \in (0,1)$ is a metric.

Let $g={d\mu _Y}/{d\mu _Y\circ T}:Y\to \mathbb {R}$ . We say that T is a Gibbs–Markov map if the following hold with respect to the countable partition $\{a\}$ :

• • $T|_a:a\to T(a)$ is a measurable bijection for each a such that $T(a)$ is the union of elements of the partition $\bmod \mu _Y$ ;

• • $\inf _a\mu _Y(T(a))>0$ (the big image property);

• • there are constants $C>0$ , $\theta \in (0,1)$ such that $|\log g(y)-\log g(y')|\le Cd_\theta (y,y')$ for all $y,y'\in a$ and for all $a\in \{a\}$ .

See for instance [A1, Ch. 4] and [AD] for background on Gibbs–Markov maps. Note that under these assumptions, since our system can be viewed as a topologically mixing countable Markov shift with $\mu _Y$ as an equilibrium state for $\log g$ , $\mu _Y$ must have positive entropy, see for example, [S2, Theorem 5.6].

Given $v:Y\to \mathbb {R}$ , let

$$ \begin{align*} D_av=\sup_{y,y'\in a,\,y\neq y'}|v(y)-v(y')|/d_\theta(y,y'),\quad |v|_\theta=\sup_{a\in\{a\}}D_a v. \end{align*} $$

The space $\mathcal {B}_\theta \subset L^\infty (\mu _Y)$ consisting of the functions $v:Y\to \mathbb {R}$ such that $|v|_\theta <\infty $ with norm $\|v\|_{\mathcal {B}_\theta }=|v|_\infty +|v|_\theta <\infty $ is a Banach space. It is known that the transfer operator $R: L^1(\mu _Y)\to L^1(\mu _Y)$ , $\int _Y R v w\, d\mu _Y=\int _Y v w\circ T\, d\mu _Y$ has a spectral gap in $\mathcal {B}_\theta $ (see, [A1, Ch. 4]). In particular, this means that $1$ is a simple eigenvalue, isolated in the spectrum of R.

We will also be interested in functions $v:Y\to \mathbb {R}$ such that there is some $C>0$ so that

(2.3) $$ \begin{align} D_av\le C\inf(1_av) \quad \text{for all } a\in\{a\}. \end{align} $$

To connect the measures preserved by Gibbs–Markov maps to the previous section, we will assume that $\log g = \bar \phi $ , so that $\mu _Y=\mu _{\bar \phi }$ is the equilibrium state for $\bar \phi $ . We will use this notation interchangeably. As in the previous section, under our assumptions, $\mu _{\bar \phi }$ will project to $\nu _\phi $ , the equilibrium state for $\phi $ .

In this section, we assume that the roof function $\tau :Y\to \mathbb {R}_{+}$ is unbounded and so that we have the following.

1. (GM0) $\mu _Y(\tau \ge x)\le c x^{-\beta }$ , $\beta>1$ for some $c>0$ depending on the map T. Moreover, we assume that $\operatorname {essinf}\tau>0$ ( $\operatorname {essinf}$ with respect to $\mu _Y$ ) and that $\tau $ satisfies equation (2.3).

The class of potentials we shall work with is as in [BTT1, BTT2], which is very natural in the unbounded roof function case. Given the suspension $Y^\tau $ and the suspension flow $F:Y^\tau \to Y^\tau $ , consider the potential $\psi : Y^\tau \to \mathbb {R}$ . Our assumptions are in terms of the induced potentials $\overline \psi (x)$ .

1. (GM1) Under assumption (GM0), we further assume that $\overline \psi =C_0-\psi _0$ , where ${0\le \psi _0 (y) \le C_1\tau ^\gamma (y)}$ , for $C_0, C_1> 0$ and $\gamma \in (\beta -1, \beta )$ . Moreover, we assume that $\operatorname {essinf}\psi _0>0$ , $\psi _0$ satisfies equation (2.3) and $\int \psi ~d\nu _\phi>0$ .

Remark 2.2. The assumption $\int \psi ~d\nu _\phi>0$ in assumption (GM1) ensures that ${p(s)>0}$ for $s>0$ , which we require throughout. Indeed, $p(s) \ge h_F(\nu _\phi )+\int \phi +s\psi ~d\nu _\phi =s \int \psi ~d\nu _\phi>0$ . In fact, standard arguments in thermodynamic formalism, see for example [PU, Theorem 4.6.5] and [S1], imply that the potentials $\phi +s\psi $ are positive recurrent for $s>0$ and right derivative $D^+p(0)= \int \psi ~d\nu _\phi $ .

We can always make $\int \psi ~d\nu _\phi $ positive by replacing $\psi $ by $\psi +c\cdot 1_Y$ for some constant c as in [BTT1, Remark 8.4]. The induced potential becomes $\bar \psi +c$ , which does not change the tail behaviour, but can make the integral strictly positive.

We note that under assumption (GM0),

(2.4) $$ \begin{align} \tau\in L^{q_0}(\mu_{\overline{\phi}})\quad\text{for any } 1\le q_0<\beta, \end{align} $$

and under assumption (GM1),

(2.5) $$ \begin{align} \psi_0\in L^{q_1}(\mu_{\overline{\phi}})\quad\text{for any } 1\le q_1<\beta/\gamma. \end{align} $$

Let $\overline \psi _n=\sum _{j=0}^{n-1}\overline \psi \circ T^j$ . We note that for $q_1>2$ (so, $\beta /\gamma>2$ ), $({\overline \psi _n-n\mu _{\overline {\phi }}(\bar \psi )})/{\sqrt n}$ converges in distribution to a Gaussian random variable with zero mean and variance $\bar \sigma ^2=\lim _{n\to \infty }({1}/{n})\int _Y (\bar \psi _n-\int _Y \bar \psi _n\,d\mu _{\overline {\phi }})^2\,d\mu _{\overline {\phi }}$ . Because $\overline \psi $ is unbounded, following [G, Theorem 3.7], to ensure that $\bar \sigma ^2> 0$ , we need to clarify two things. (We recall that R is the transfer operator for T with spectral gap in $\mathcal {B}_\theta $ .) Given $\overline \psi =C_0-\psi _0$ with $q_1>2$ (so, $\beta /\gamma>2$ ), let $\Phi =\overline \psi -\int _Y \overline \psi \, d\mu _{\overline {\phi }}$ .

We will also require:

1. (a) $R(\Phi v)\in \mathcal {B}_\theta $ for all $v\in \mathcal {B}_\theta $ ;

2. (b) there exists no function $h\in \mathcal {B}_\theta $ so that $\Phi =h-h\circ T$ .

Remark 2.3. Item (a) is verified (in the setup of Gibbs–Markov maps) inside the proof of Lemma 3.1 below (see, in particular, equation (3.4)). Item (b) simply requires that $\overline \psi $ is not cohomologous to a constant. As soon as $\overline \psi $ (equivalently $\psi $ ) is not cohomologous to a constant, equation (2.6) below ensures that $\sigma ^2>0$ .

A classical lifting scheme [MTo] ensures that the CLT holds for the original potential $\psi :Y^\tau \to Y^\tau $ with mean zero and non-zero variance $\sigma ^2$ . In this case, given that ${\nu _{\phi }=({\mu _{\overline {\phi }}\times m|_{Y^\tau }})/{\int _Y\tau \,d\mu _{\overline {\phi }}}}$ is the unique equilibrium state for $\phi $ (this is a classical lifting scheme: see for instance, the review in [BTT2, §3]), let

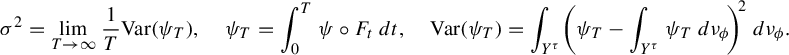$$ \begin{align*} \sigma^2 &= \lim_{T\to\infty}\frac{1}{T}\textrm{Var}(\psi_T),\quad \psi_T=\int_{0}^T\psi\circ F_t\, dt,\quad \textrm{Var}(\psi_T)=\int_{Y^\tau}\kern-2.2pt\bigg(\psi_T-\int_{Y^\tau}\psi_T\, d\nu_{\phi}\kern-1.4pt\bigg)^{\kern-1.5pt 2}\, d\nu_{\phi}. \end{align*} $$

It follows from [MTo] that, for $\tau ^* := \int _Y \tau \, d\mu _{\bar \phi }$ ,

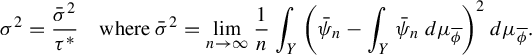(2.6) $$ \begin{align} \sigma^2=\frac{\bar\sigma^2}{\tau^*}\quad \text{where }\bar\sigma^2=\lim_{n\to\infty}\frac{1}{n}\int_Y \bigg(\bar\psi_n-\int_Y \bar\psi_n\,d\mu_{\overline{\phi}}\bigg)^2\,d\mu_{\overline{\phi}}. \end{align} $$

We also write $\sigma _{\nu _\phi }(\psi )^2$ when we wish to emphasise the dependence on $\phi $ and $\psi $ .

2.3 Key propositions

Note that, in general, the derivatives $p'(s), p"(s)$ of our pressure functions are not defined at $s=0$ : we will be interested in the derivatives from the right, but to save notation, we will write $p'(0), p"(0)$ and so on, rather than $D^+p(0), (D^2)^+p(0)$ . Similarly for the function $q_{\phi , \psi }$ used later. Combining and adapting arguments from [BTT1, BTT2, MT], we obtain the following result.

Proposition 2.4. Assume assumptions (GM0) and (GM1). Assume that $q_0\in [1,\beta )$ and $q_1\in [1,\beta /\gamma )$ . Then, there exists $\delta _0>0$ so that for all $u,s\in [0,\delta _0)$ :

1. (i) $\bar p(u,s):=P_{T}(\overline {\phi +s\psi -u})$ is $C^{q_0}$ in u and $C^{q_1}$ in s;

2. (ii) define $p(s):=P_{F}(\phi +s\psi )$ . Then,

   $$ \begin{align*} p(s)=\frac{\bar p(0,s)}{\tau^*}(1+o(1))\quad \text{as } s\to 0. \end{align*} $$

   Also, $p(s)$ is $C^{q_1}$ and $p'(0)={\overline {\psi }^*}/{\tau ^*}:={\int _Y\overline {\psi }\, d\mu _{\bar \phi }}/{\int _Y\tau \, d\mu _{\bar \phi }}$ ;

3. (iii) suppose $q_1>2$ . Then $p"(0)=\sigma ^2$ , where $\sigma ^2=\sigma _{\nu _\phi }(\psi )^2$ is as in equation (2.6).

Remark 2.5. We note that the restrictions posed on the class of potentials considered in assumption (GM1) is not just a matter of simplification. Hypothesis (GM1) or variants of it are needed to ensure that the transfer operators perturbed with real valued potentials defined in §3 are well defined in $\mathcal {B}_\theta $ . This is a necessary ingredient for the relation between eigenvalues and pressure function: see §3 below.

As we will show in §3, item (ii) of Proposition 2.4 follows from item (i) together with the implicit function theorem (IFT). For the case of LSV maps (as in [LSV]; they are a type of AFN map, see §7) with infinite measure, an implicit equation is exploited in the proof of [BTT1, Proof of Theorem 4.1]. For the proof of item (i), we adapt the arguments in [BTT1] to the case of finite measure. For the proof of item (ii), we combine the ‘implicit’ equation in [BTT1, Proof of Theorem 4.1] with the IFT, which is natural since here we are interested in the smoothness of $P_{T}(\overline {\phi +s\psi })$ .

While Proposition 2.4 will allow us to obtain the expected EKP inequality for $q_1>3$ (so $\beta /\gamma> 3$ , see equation (2.5)), in the case $\beta /\gamma <3$ , we need a refined version under stronger assumptions. The next proposition tells us how the second derivative of $p(s)$ blows up as $s\to 0$ when $\beta /\gamma \in (1,2]$ and how the third derivative blows up as $s\to 0$ when $\beta /\gamma \in (2,3)$ . (It also gives the speed of convergence of the first and second derivatives to $p'(0)$ and $p"(0)$ , respectively.)

Proposition 2.6. Assume assumption (GM0) with $\mu _Y(\tau \ge x)=c x^{-\beta }(1+o(1))$ for $\beta \in (1,2)$ . Suppose that assumption (GM1) holds with $\psi _0=C_1 \tau ^\gamma $ with $\gamma \in (\beta -1,1)$ . There exist $C_2, C_3>0$ depending only on $c,\beta ,\gamma $ and $\tau ^*$ so that the following hold as $s\to 0$ .

1. (i) If $\beta /\gamma \in (1,2]$ , then $p"(s)=C_2 s^{\beta -\gamma -1}(1+o(1))$ .

2. (ii) If $\beta /\gamma \in (2, 3)$ , then $p"'(s)=-C_3 s^{\beta -2\gamma -1}(1+o(1))$ .

Remark 2.7.

1. (i) It is possible to change the assumption on $\beta $ and $\gamma $ , but we need a definite assumption to state a final result. When $\gamma>1$ , the asymptotics are different. We do not consider other cases here as this would make the analysis even more tedious, though most of the calculations can easily be adapted to fit this case.

2. (ii) If $\gamma =1$ and $\beta>1$ , then we have the following scenarios: (a) $p"(s)=C_2 s^{\beta -2}(1+o(1))$ if $\beta \in (1,2)$ , (b) $p"(s)=C_3 \log (1/s)(1+o(1))$ if $\beta =2$ and (c) $p"'(s)=C_4 s^{\beta -3}(1+o(1))$ if $\beta \in (2,3)$ . We do not display the calculations in this case mainly because it does not lead to any interesting phase transition in the corresponding version of Theorem 2.9.

2.4 Main theorems

Using Propositions 2.4 and 2.6, we obtain an interesting generalisation of [RS] for the restricted pressure $q_{\phi , \psi }$ . Though our class of potentials is, naturally, much more restricted than in assumption (GM1), Theorems 2.8 and 2.9 below show the existence of a new phase transition in terms of whether $\psi _0$ is in $L^{2}(\mu _{\overline {\phi }})$ or not. In particular, if $\beta /\gamma>2$ , then $\psi _0$ is $L^2(\mu _{\overline {\phi }})$ (recall equation (2.5)). The new phase transition is captured in Theorem 2.9.

The result below gives the EKP inequality for $q_1>3$ (with $q_1$ as in equation (2.5)) when the CLT holds. Before the statement, we note that we are interested in cases $\int \psi ~d\nu \neq \int \psi ~d\nu _\phi $ , so implicitly, we are always assuming that $\psi $ is not cohomologous to a constant. We also recall from Remark 2.3 that this is all we need to ensure that $\sigma ^2>0$ .

Theorem 2.8. Assume assumptions (GM0) and (GM1). Assume that $q_1>3$ (so ${\beta /\gamma> 3}$ ) and let $\sigma =\sigma _{\nu _\phi }(\psi )$ be as defined in equation (2.6). There exists ${\epsilon }>0$ so that for any F-invariant probability measure $\nu $ with $\int \psi ~d\nu \in (\int \psi ~d\nu _\phi , \int \psi ~d\nu _\phi +{\epsilon })$ , we have

$$ \begin{align*} \int\psi\,d\nu-\int\psi\,d\nu_{\phi} \le C_{\phi, \psi} {\sqrt 2}\sigma\sqrt{P_{\nu_\phi}(\phi)-P_\nu(\phi)}, \end{align*} $$

where $C_{\phi , \psi } \geq 1$ tends to $1$ as $\int \psi \, d\nu \to \int \psi \, d\nu _{\phi }$ .

For the equilibrium states $\nu _s$ of $\phi + s\psi $ , we have

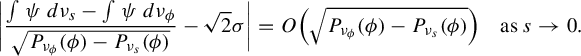(2.7) $$ \begin{align} \bigg| \frac{\int\psi\,d\nu_s-\int\psi\,d\nu_{\phi} }{ \sqrt{P_{\nu_\phi}(\phi)-P_{\nu_s}(\phi)}} - \sqrt 2 \sigma \bigg| = O\Big(\sqrt{P_{\nu_\phi}(\phi)-P_{\nu_s}(\phi)} \Big) \quad \text{as } s \to 0. \end{align} $$

The first result below addresses the case $q_1<3$ . We consider two main cases for the ratio $\beta /\gamma $ . It is precisely this result that captures the new type of phase transition. While item (b) of the result below shows a (familiar) EKP inequality in the case $\beta /\gamma \in (2,3)$ (when the CLT with standard scaling is present), item (a) gives a new type of EKP inequality with the exponent changing from $1/2$ to one depending on the ratio $\beta /\gamma $ . The transition is natural (see Remark 2.11).

Theorem 2.9. Assume assumption (GM0) with $\mu _Y(\tau \ge x)=c x^{-\beta }(1+o(1))$ , with ${\beta \in (1,2)}$ . Suppose that assumption (GM1) holds with $\psi _0=C_1 \tau ^\gamma $ with $\gamma \in (\beta -1,1)$ .

There exist ${\epsilon }>0$ and constants $c_2, c_3>0$ so that the following hold for any F-invariant probability measure $\nu $ with $\int \psi ~d\nu \in (\int \psi ~d\nu _\phi , \int \psi ~d\nu _\phi +{\epsilon })$ .

1. (a) If $\beta /\gamma \in (1,2]$ , then

   $$ \begin{align*} \int\psi\,d\nu-\int\psi\,d\nu_{\phi}\le c_2 (P_{\nu_\phi}(\phi)-P_\nu(\phi))^{({\beta-\gamma})/({\beta-\gamma+1})}. \end{align*} $$

   For the equilibrium states $\nu _s$ of $\phi + s\psi $ , there is a constant (for $C_2$ as in Proposition 2.6(i)) $C_2>0$ such that

   (2.8) $$ \begin{align} \bigg| \frac{ \int\psi\,d\nu_s-\int\psi\,d\nu_{\phi}}{(P_{\nu_\phi}(\phi)-P_{\nu_s}(\phi))^{({\beta-\gamma})/({\beta-\gamma+1})} } - \frac{\beta}{\gamma} C_2^{-{1}/({\beta-\gamma})} \bigg| = o(1) \quad \text{as } s \to 0. \end{align} $$

2. (b) If $\beta /\gamma \in (2,3)$ , then

   $$ \begin{align*} \int\psi\,d\nu-\int\psi\,d\nu_{\phi}\le c_3 {\sqrt 2}\sigma\sqrt{P_{\nu_\phi}(\phi)-P_\nu(\phi)}. \end{align*} $$

   For the equilibrium states $\nu _s$ of $\phi + s\psi $ , we have

   (2.9) $$ \begin{align} \bigg| \frac{ \int\psi\,d\nu_s- \int\psi\,d\nu_{\phi}}{\sqrt{P_{\nu_\phi}(\phi)-P_{\nu_s}(\phi)}} - \sqrt2\sigma \bigg| = O((P_{\nu_\phi}(\phi)-P_{\nu_s}(\phi) )^{({\beta-2\gamma})/{2}}) \quad \text{as } s \to 0. \end{align} $$

Remark 2.10. We note that $P_{\nu _\phi }(\phi )-P_{\nu }(\phi )$ in the theorems above cannot be zero because $\nu _\phi \neq \nu $ and $\nu _\phi $ is the unique equilibrium state for $\phi $ . Similarly, $P_{\nu _\phi }(\phi )-P_{\nu _s}(\phi )$ cannot be zero because $\nu _\phi \neq \nu _s$ for $s>0$ .

Remark 2.11.

1. (a) Recall that $\overline \psi _n=\sum _{j=0}^{n-1}\overline \psi \circ T^j$ and that $\psi _T=\int _0^T\psi \circ F_t\, dt$ . It is known (see for instance [S1, Theorem 2]) that in the setup of Theorem 2.9(a) with $\beta /\gamma <2$ , $({\overline \psi _n-n\int _{Y}\overline \psi \, d\mu _Y}/{n^{\gamma /\beta }})\to ^d M_{\beta /\gamma }$ , where $M_{\beta /\gamma }$ is a random variable in the domain of a stable law with index $\beta /\gamma <2$ . This lifts to a similar limit law for the flow (see for instance [BTT2, Lemma 6.3]): $({\psi _T-T\int _{Y^\tau }\psi \, d\nu }/{T^{\gamma /\beta }})\to ^d M_{\beta /\gamma }$ .

   In the setup of Theorem 2.9(a) with $\beta /\gamma =2$ , $({\overline \psi _n-n\int _{Y}\overline \psi \, d\mu _Y}/{\sqrt {n\log n}})\to ^d \mathcal N(0,\sigma _0^2)$ for some non-zero $\sigma _0$ (see [S1, Theorem 3]). This is a Gaussian limit but with non-standard scaling $\sqrt {n\log n}$ . The same type of limit lifts to the flow (see for instance [BTT2, Lemma 6.3]).

   In either of these two cases, that is, $\beta /\gamma \in (1,2]$ in Theorem 2.9(a), the leading Hölder exponent depends on $\beta $ and $\gamma $ .

   As soon as one has a CLT with standard normalisation $\sqrt {n}$ , as in Theorem 2.9(b), the leading Hölder exponent is $1/2$ , independent of $\beta $ and $\gamma $ . Theorem 2.9 captures the transition from a stable law to the CLT with standard scaling in terms of the Hölder continuity of the pressure (in the weak ${^*}$ norm): the change in the Hölder exponent makes this precise.

2. (b) We believe that some version of Theorem 2.9(a) persists if one weakens the assumption to $\psi _0\in (C_1 \tau ^\gamma , C_2\tau ^\gamma )$ with $C_1, C_2>0$ , and even under weaker assumptions on the tail of $\tau $ . In addition to the need to control the precise upper and lower bounds for $p'(s)-p'(0)$ in Proposition 2.6(a) (which make the calculations seriously more cumbersome), one needs to ensure that $p"(s)>0$ . This is very heavy in terms of calculations without assumptions that ensure regular variation of $\psi _0$ . We do not pursue this here.

Remark 2.12. We can interpret equations (2.8) and (2.9) in Theorem 2.9(b) as follows: the pressure function has a polynomial (in fact quadratic) form for $\beta /\gamma \in (2,3)$ , but as $\beta /\gamma $ drops below $2$ , then the Hölder exponent jumps to $(\beta -\gamma +1)/(\beta -\gamma )> 1+1/\gamma > 2$ . This gives a kink in the second derivative of the pressure as a function of the weak $^*$ -norm of the measures. This represents a phase transition of order $3$ if $(\beta -\gamma +1)/(\beta -\gamma ) \in (2,3)$ or of higher order if $(\beta -\gamma +1)/(\beta -\gamma ) \geq 3$ .

Remark 2.13. The EKP formula can fail to hold under our assumptions (GM0) and (GM1), when $\int \psi ~d\nu <\int \psi ~d\nu _\phi $ . We demonstrate this for the Pomeau–Manneville map $f_\alpha :x \mapsto x(1+x^\alpha ) \bmod 1$ on the unit interval with $\alpha \in (0,1)$ . The induced map $T = f_\alpha ^\tau $ on the domain Y of the second branch is a full-branched Gibbs–Markov map. The potential $\phi = \log f^{\prime }_\alpha $ , so $\bar \phi = \log T'$ , satisfies $P(\phi )=0$ and the equilibrium measure $\mu _{\bar \phi }$ is a Gibbs measure with $n^{-(\beta +1)}\ll \mu _{\bar \phi }(\tau = n) \ll n^{-(\beta +1)}$ for $\beta = 1/\alpha $ . Take the potential $\psi = C_0 \cdot 1_Y - C_1$ for some $C_0, C_1> 0$ , so $\bar \psi (y) = C_0-\psi _0(y) = C_0-C_1\tau (y)$ , where $C_0$ is sufficiently large that $\int \psi ~d\nu _\phi>0$ .

The partition $\{ a_k \}$ of T has exactly one interval $a_k$ with $\tau |_{a_k} = k$ for each $k \geq 1$ . Let $x_k \in a_k$ be such that $T(x_k) = x_k$ and let $\nu _k$ be the equidistribution on the orbit of $x_k$ under $f_\alpha $ . The Gibbs property of $\mu _{\bar \phi }$ , recalling that we assume $P(\phi )=0$ , implies that $e^{\bar \phi (x_k)} \gg \mu _{\bar \phi }(a_k) \gg k^{-(\beta +1)}$ , so $\bar \phi (x_k) \ge \log c - (\beta +1)\log k$ for some $c> 0$ .

The lift of $\nu _k$ is the Dirac measure at $x_k$ , so Abramov’s formula gives $\int \phi ~d\nu _k = { \delta _{x_k}(\bar \phi )}/ { \delta _{x_k}(\tau )} \geq ({\log c - (\beta +1)\log k})/{k}$ . Since also $h_{\nu _k}(f_\alpha ) = 0$ , we get

$$ \begin{align*} 0 = P(\phi) \geq P_{\nu_k}(\phi) = h_{\nu_k}(f_\alpha) + \int\phi~d\nu_k \ge \frac{1}{k}( \log c - (\beta+1)\log k)\to 0. \end{align*} $$

Finally, notice that

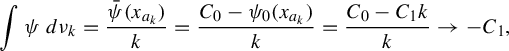$$ \begin{align*} \int\psi~d\nu_k =\frac{\bar\psi(x_{a_k})}{k} = \frac{C_0-\psi_0(x_{a_k})}{k} = \frac{C_0-C_1 k}{k}\to -C_1, \end{align*} $$

as $k \to \infty $ . Hence, for any $C, \rho>0$ , we can find k such that

$$ \begin{align*} \int\psi~d\nu_\phi-\int\psi~d\nu_k> C( P(\phi)-P_{\nu_k}(\phi))^\rho, \end{align*} $$

violating the EKP.

We stress that for other systems for which an induced map is a Gibbs–Markov system with polynomial tail, we generally expect the same type of argument as above can be performed: the key, natural, requirement is that $\mu _{\bar \phi }(a_k) \gg k^{-(\beta +1)}$ for some infinite sequence of k.

We close this remark by pointing out that in this example, the pressure function is not differentiable at 0. Indeed, for any $s < 0$ , there is $k \in \mathbb {N}$ such that $p(s) = P(\phi + s\psi ) \geq \int \phi + s \psi ~d\nu _k> -s C_1 - s^2$ . Therefore, the left derivative of $p(s)$ at zero is

$$ \begin{align*} \lim_{s \nearrow 0} \frac{p(s)-p(0)}{s} \leq \lim_{s \nearrow 0} {-C_1-s} = -C_1 < 0. \end{align*} $$

For $s \geq 0$ , we have

$$ \begin{align*} p(s) = P(\phi + s\psi) \geq \int \phi + s \psi~d\nu_\phi = P(\phi) + \int s \psi~d\mu_\phi = s \int \psi~d\nu_\phi, \end{align*} $$

so the graph of the pressure function lies above a line with slope $\int \psi ~d\nu _\phi $ . Recall that we chose $C_0, C_1> 0$ such that $\int \psi ~d\nu _\phi> 0$ , so this slope is positive. Since also the pressure function is convex, this implies that $p(s)$ is increasing for $s \geq 0$ and $p'(s) \geq \int \psi ~ d\nu _\phi> 0$ . However, the left derivative of p at $s = 0$ is negative so p is not differentiable at $s=0$ .

Finally, we give an analogue of [RS, Theorem 7.1] in our setting, which handles the case when $\int \psi ~d\nu $ is far from $\int \psi ~d\nu _\phi $ . Note that our constant $C_{\phi , \psi }^{\prime }$ is not very refined here, but also that we are dealing with some cases of unbounded potentials $\psi $ , so we would not expect as much control as when we have boundedness.

Theorem 2.14. Assume assumptions (GM0) and (GM1). In the setup of Theorems 2.8 and 2.9(b), let $\rho =1/2$ . In the setup of Theorem 2.9(a), let $\rho =({\beta -\gamma })/({\beta -\gamma +1})$ .

There exists $C_{\phi , \psi }^{\prime }>0$ so that for any F-invariant probability measure $\nu $ with $\int \psi ~d\nu> \int \psi ~d\nu _\phi $ , we have

$$ \begin{align*} \int\psi\,d\nu-\int\psi\,d\nu_{\phi} \le C_{\phi, \psi}^{\prime}(P_{\nu_\phi}(\phi)-P_\nu(\phi))^\rho. \end{align*} $$

3 Proof of Proposition 2.4

As is customary in the literature, due to the Ruelle–Perron–Frobenius (RPF) theorem, in the setup of Gibbs–Markov maps $T:Y\to Y$ (see for instance [BTT1, §3.3]), the study of the pressure function $P_{T}(\overline {\phi +s\psi })$ comes down to the study of a perturbed version of the transfer operator $R:L^1(\mu _{\bar \phi })\to L^1(\mu _{\bar \phi })$ . In particular, we identify $P_{T}(\overline {\phi +s\psi -u})$ , $u\in [0,\delta )$ , $s\in (0,\delta )$ for some $\delta>0$ with $\log \unicode{x3bb} (u,s)$ , where $\unicode{x3bb} (u,s)$ is the leading eigenvalue of the perturbed transfer operator

$$ \begin{align*} R(u,s) v=R(e^{-u\tau} e^{s\overline{\psi}} v), \quad u, s \in [0,\delta_0),\ v\in L^1(\mu_{\bar\phi}). \end{align*} $$

Note that by the argument at the end of Remark 2.2 coupled with Abramov’s formula, $\int \psi ~d\nu _\phi>0$ implies that $P_T(\overline {\phi +s\psi })>0$ for $s>0$ . We briefly recall the application of the RPF theorem. Note that $R(0,0)=R$ for $u=s=0$ . We already know that R has a spectral gap in $\mathcal {B}_\theta $ ; in particular, this means that $1$ is a simple eigenvalue, isolated in the spectrum of R. Under assumption (GM1), there exists $\delta _0>0$ so that $\|R(u,s)-R(u,0)\|_{\mathcal {B}_\theta }\ll s^{\epsilon }$ for some ${\epsilon }>0$ and all $u, s \in [0,\delta _0)$ . The proof of this fact is standard; for instance, it is an easier version of [BTT1, Proof of Lemma 5.2] ( $\beta <1$ there gives some ${\epsilon }>0$ here). In fact, much more is true: see Lemma 3.1 below. Since we also know that $u\mapsto R(u,0)$ is analytic in $u\in [0,\delta _0)$ , there exists a family of eigenvalues $\unicode{x3bb} (u,s)$ analytic in $u\in [0,\delta _0)$ and $C^1$ in $s\in [0,\delta _0)$ with $\unicode{x3bb} (0,0)=1$ . By the RPF theorem,

(3.1) $$ \begin{align} \bar p(u,s)=P_{T}(\overline{\phi+s\psi -u})=\log\unicode{x3bb}(u,s), \quad u, s\in [0,\delta_0). \end{align} $$

To study the smoothness of $\unicode{x3bb} (u,s)$ , as a function of u and s, we need to recall some facts about the smoothness of $R(u,s)$ .

For non-integer $q_{*}\in \mathbb {R}_{+}$ , we write $[q_{*}]$ for the integer part and say that a function $g:\mathbb {R}\to \mathbb {R}$ is $C^{q_*}$ if $|g|_{C^{[q_{*}]}}<\infty $ and $\sup _{x_1\neq x_2} |x_1-x_2|^{-(q_{*}-[q_{*}])}|({\partial ^{[q^*}}/{\partial x^{[q_*]}})g(x_1)-({\partial ^{[q^*]}}/{\partial x^{[q_*]}})g(x_2)|<\infty $ . In a similar manner, we talk about the smoothness of ${s\to R(u,s)}$ and $u\to R(us,s)$ . The statement of Lemma 3.1 below makes this precise.

Let $q_0$ and $q_1$ be as in equations (2.4) and (2.5). Throughout, we write

(3.2) $$ \begin{align} G_{[q_0]}(u,s)=\frac{\partial^{[q_0]}}{\partial u^{[q_0]}}R(u,s),\quad H_{[q_1]}(u,s)=\frac{\partial^{[q_1]}}{\partial s^{[q_1]}}R(u,s) \end{align} $$

and

(3.3) $$ \begin{align} K_{[q_1]}(u,s)=\frac{\partial^{[q_1]}}{\partial s^{[q_1]}}\frac{\partial}{\partial u} R(u,s). \end{align} $$

Lemma 3.1. Assume assumptions (GM0) and (GM1). Let $q_0$ and $q_1\in [1,\beta /\gamma )$ be so that equations (2.4) and (2.5) hold.

Let G, H and K be as in equations (3.2) and (3.3). Let $u, s \in [0,\delta _0)$ . Then, $\|G_{[q_0]}(u,s)\|_{\mathcal {B}_\theta }<\infty $ and $\|H_{[q_1]}(u,s)\|_{\mathcal {B}_\theta }<\infty $ . Moreover, there exists $C>0$ so that:

1. (i) for all $u_1,u_2,s_1,s_2\in [0, \delta _0)$ ,

   $$ \begin{align*} \|G_{[q_0]}(u_1,s)-G_{[q_0]}(u_2,s)\|_{\mathcal{B}_\theta}\le C|u_1-u_2|^{q_0-[q_0]}, \end{align*} $$
   $$ \begin{align*}\|H_{[q_1]}(u,s_1)-H_{[q_1]}(u,s_2)\|_{\mathcal{B}_\theta}\le C|s_1-s_2|^{q_1-[q_1]}; \end{align*} $$

2. (ii) for all $u>0$ and $s_1,s_2 \in [0,\delta _0)$ , $ \|K_{[q_1]}(u,s)\|_{\mathcal {B}_\theta }\le C u^{\beta -q_1\gamma -1} $ and

   $$ \begin{align*} \|K_{[q_1]}(u,s_1)-K_{[q_1]}(u,s_2)\|_{\mathcal{B}_\theta}\le C|s_1-s_2|^{q_1-[q_1]}\cdot u^{\beta-q_1\gamma-1}. \end{align*} $$

Remark 3.2. Recall that under assumption (GM1), $\gamma>\beta -1$ . Hence, $q_1\in [1,\beta /\gamma )$ is so that $\beta -q_1\gamma <1$ . This means that in Lemma 3.1(ii), the factor in u blows up as $u\to 0$ , but in a controlled way.

Proof. The first statements on $G_{[q_0]}(u,s)$ and $H_{[q_1]}$ follow immediately from [MT, Proposition 12.1]. Assumption (A1) there is part of assumptions (GM0), (GM1) here and the involved constants depend on the $L^{q_0}(\mu _{\overline {\phi }}), L^{q_1}(\mu _{\overline {\phi }})$ norm of $\tau ,\bar \psi $ , respectively, on $\theta \in (0,1)$ and on the constants in assumptions (GM0), (GM1).

We sketch the argument for the statement on $H_{[q_1]}$ and, as a consequence, the somewhat easier fact that $G_{[q_0]}(u,s)$ is $C^{q_1}$ in s. By the argument used in the proof of [MT, Proposition 12.1], for $w\in L^1(\mu _{\overline {\phi }})$ with $\operatorname {essinf} w>0$ and satisfying equation (2.3), we obtain

(3.4) $$ \begin{align} \|R(w\,v)\|_{\mathcal{B}_\theta}\le C |w|_{L^1(\mu_{\overline{\phi}})}|v|_{\theta} \end{align} $$

for some $C>0$ depending on the constant appearing in equation (2.3).

Under assumption (GM1), $\psi _0\in L^{q_1}(\mu _{\overline {\phi }})$ . Since $H_{[q_1]}(u,s)\tilde v=R(\bar \psi ^{[q_1]} e^{-u\tau } e^{s C_0} e^{-s\psi _0}\tilde v)$ , the first statement on $H_{[q_1]}$ follows immediately from equation (3.4) with $w=\bar \psi ^{[q_1]}$ and $v=e^{-u\tau } e^{s C_0}e^{-s\psi _0}\tilde v$ . Throughout the rest of the proof, we will heavily exploit equation (3.4), but we will not write down the explicit form of w and v.

Proof of item (i). Using equation (3.4), we compute that

$$ \begin{align*} \|(H_{[q_1]}(u,s_1)&-H_{[q_1]}(u,s_2))v\|_{\mathcal{B}_\theta}\\ &\le \|R(\bar\psi^{[q_1]}(e^{s_1 C_0}-e^{s_2 C_0})e^{-s_1\psi_0}e^{-u\tau} v)\|_{\mathcal{B}_\theta}\\ &\quad +\|R(\bar\psi^{[q_1]}(e^{-s_1 \psi_0}-e^{-s_2 \psi_0})e^{s_2C_0}e^{-u\tau}v)\|_{\mathcal{B}_\theta}\\ &\le C_0|s_1-s_2|\|R(\bar\psi^{[q_1]} e^{-s\psi_0}v)\|_{\mathcal{B}_\theta}\\ &\quad + C|\bar\psi^{[q_1]}(e^{-s_1 \psi_0}-e^{-s_2 \psi_0})e^{-u\tau}|_{L^1(\mu_{\overline{\phi}})}|v|_{\theta}\\ &\le C'|s_1-s_2|\,|\bar\psi^{[q_1]}|_{L^1(\mu_{\overline{\phi}})}|v|_{\theta}+ C|\bar\psi^{[q_1]}(e^{-s_1 \psi_0}-e^{-s_2 \psi_0})e^{-u\tau}|_{L^1(\mu_{\overline{\phi}})}|v|_{\theta} \end{align*} $$

for some $C, C'>0$ .

The second statement on $H_{[q_1]}$ follows since

$$ \begin{align*} |\bar\psi^{[q_1]}(e^{-s_1 \psi_0}-e^{-s_2 \psi_0}) e^{-u\tau}|_{L^1(\mu_{\overline{\phi}})} \ll|s_1-s_2|^{q_1-[q_1]}\, |\psi_0^{q_1}|_{L^{1}(\mu_{\overline{\phi}})}\ll |s_1-s_2|^{q_1-[q_1]}. \end{align*} $$

Proof of item (ii). First, $K_{[q_1]}(u,0)=-R(\bar \psi ^{[q_1]}\tau e^{-u\tau })$ . Using equation (3.4), $ \|(K_{[q_1]}(u,0)v\|_{\mathcal {B}_\theta }\le C|\bar \psi ^{[q_1]}\tau e^{-u\tau } |_{L^1(\mu _{\overline {\phi }})}. $ To estimate this quantity, let ${S(x)=\mu _{\overline {\phi }}(\tau>x)}$ and recall from Remark 3.2 that $\beta -q_1\gamma <1$ . Integrating by parts and using assumption (GM0),

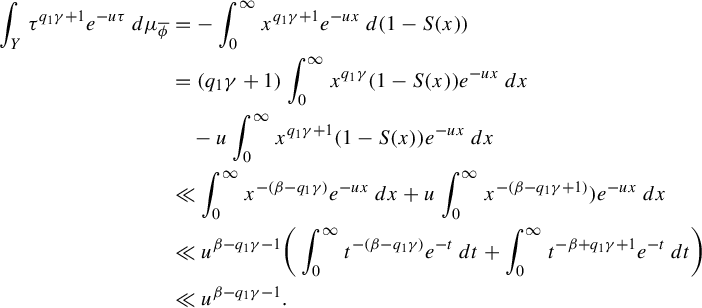(3.5) $$ \begin{align} \nonumber \int_Y \tau^{q_1\gamma+1} e^{-u\tau}\, d\mu_{\overline{\phi}}&=- \int_0^{\infty} x^{q_1\gamma+1} e^{-ux}\, d(1-S(x))\\ \nonumber &=(q_1\gamma+1)\int_0^\infty x^{q_1\gamma}(1-S(x)) e^{-ux}\, d x\\ \nonumber &\quad-u\int_0^\infty x^{q_1\gamma+1}(1-S(x)) e^{-ux}\, d x \\ \nonumber &\ll \int_0^\infty x^{-(\beta-q_1\gamma)} e^{-ux}\, d x+u\int_0^\infty x^{-(\beta-q_1\gamma+1)})e^{-ux}\, d x\\ &\ll u^{\beta-q_1\gamma-1} \bigg( \int_0^\infty t^{-(\beta-q_1\gamma)} e^{-t}\, d t+ \int_0^\infty t^{-\beta+q_1\gamma+1} e^{-t}\, d t\bigg) \nonumber \\ &\ll u^{\beta-q_1\gamma-1}. \end{align} $$

Hence, $\|(K_{[q_1]}(u,0)v\|_{\mathcal {B}_\theta }\le Cu^{\beta -q_1\gamma -1}$ , as claimed.

Using that $K_{[q_1]}(u,s)=-R(\bar \psi ^{[q_1]}\tau e^{-u\tau } e^{s C_0}e^{-s\psi _0})$ , we compute that

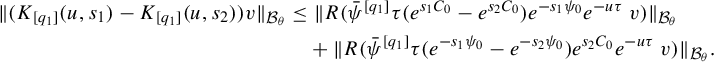$$ \begin{align*} \|(K_{[q_1]}(u,s_1)-K_{[q_1]}(u,s_2))v\|_{\mathcal{B}_\theta} &\le \|R(\bar\psi^{[q_1]}\tau(e^{s_1 C_0}-e^{s_2 C_0})e^{-s_1\psi_0}e^{-u\tau}\, v)\|_{\mathcal{B}_\theta}\\ &\quad +\|R(\bar\psi^{[q_1]}\tau(e^{-s_1 \psi_0}-e^{-s_2 \psi_0})e^{s_2C_0}e^{-u\tau}\, v)\|_{\mathcal{B}_\theta}. \end{align*} $$

Using equation (3.4), we obtain that there exists $C>0$ so that

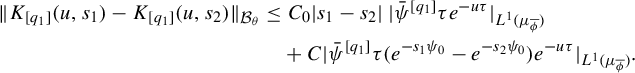(3.6) $$ \begin{align} \nonumber\|K_{[q_1]}(u,s_1)-K_{[q_1]}(u,s_2)\|_{\mathcal{B}_\theta}&\le C_0|s_1-s_2|\, |\bar\psi^{[q_1]}\tau e^{-u\tau}|_{L^1(\mu_{\overline{\phi}})}\\ &\quad +C|\bar\psi^{[q_1]}\tau(e^{-s_1 \psi_0}-e^{-s_2 \psi_0})e^{-u\tau}|_{L^1(\mu_{\overline{\phi}})}. \end{align} $$

Regarding the first term in equation (3.6), recall assumption (GM1) and note that $|\bar \psi ^{[q_1]}\tau e^{-u\tau }|_{L^1(\mu _{\overline {\phi }})}\ll |\tau ^{q_1\gamma +1} e^{-u\tau }|_{L^1(\mu _{\overline {\phi }})}$ . This together with equation (3.5) implies that the first term in equation (3.6) is bounded by $|s_1-s_2|\, u^{\beta -q_1\gamma -1}$ .

It remains to estimate the second term in equation (3.6). Using assumption (GM1), compute that

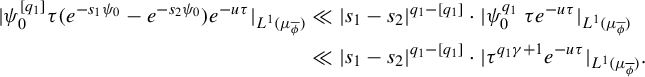$$ \begin{align*} |\psi_0^{[q_1]}\tau(e^{-s_1 \psi_0}-e^{-s_2 \psi_0})e^{-u\tau}|_{L^1(\mu_{\overline{\phi}})} &\ll |s_1-s_2|^{q_1-[q_1]}\cdot|\psi_0^{q_1}\,\tau e^{-u\tau}|_{L^1(\mu_{\overline{\phi}})}\\ &\ll |s_1-s_2|^{q_1-[q_1]}\cdot|\tau^{ q_1\gamma+1} e^{-u\tau}|_{L^1(\mu_{\overline{\phi}})}. \end{align*} $$

By equation (3.5), $|\tau ^{ q_1\gamma +1} e^{-u\tau }|_{L^1(\mu _{\overline {\phi }})}\ll u^{\beta -q_1\gamma -1}$ and the conclusion follows.

A consequence of Lemma 3.1 is that the family of eigenvalues $\unicode{x3bb} (u,s)$ has ‘good’ smoothness properties. Recall that $\tau ^*,\bar \psi ^*$ are as in Proposition 2.4(ii).

Corollary 3.3. The following hold in the setup of Lemma 3.1. Let $u, s\in [0,\delta _0)$ .

1. (i) $\unicode{x3bb} (u,s)=1+g(u,s)$ , where $g(u,s)\to 0$ as $u,s\to 0$ and $g(u,s)$ is $C^{q_0}$ in u and $C^{q_1}$ in s.

2. (ii) $({\partial }/{\partial u})\unicode{x3bb} (u,s)=-\tau ^*+d(u,s)$ , where $d(u,s)$ is $C^{q_0-1}$ in u and $C^{q_1}$ in s and $d(u,0)\to 0$ as $u\to 0$ . Moreover, $({\partial }/{\partial s})\unicode{x3bb} (u,s)=\bar \psi ^*+e(u,s)$ , where $e(u,s)$ is $C^{q_0}$ in u and $C^{q_1-1}$ in s and $e(u,s)\to 0$ as $u,s\to 0$ .

3. (iii) Let $\kappa (u,s)=({\partial }/{\partial s})({\partial }/{\partial u})\unicode{x3bb} (u,s)$ . Then, for all $u,s\in [0,\delta _0)$ , $ |\kappa (u,s)|\le C u^{\beta -q_1\gamma -1} $ and $\kappa (u,s)$ is $C^{q_1-1}$ in s.

Proof. (i) Given that $v(u,s)$ is the normalised eigenvector corresponding to $\unicode{x3bb} (u,s)$ ,

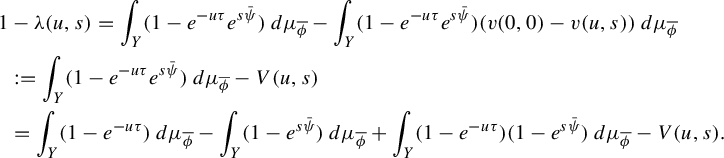(3.7) $$ \begin{align}~ \nonumber 1 &-\unicode{x3bb}(u,s) =\int_Y (1-e^{-u\tau}e^{s\bar\psi})\, d\mu_{\overline{\phi}} -\int_Y (1-e^{-u\tau}e^{s\bar\psi})(v(0,0)-v(u,s))\, d\mu_{\overline{\phi}}\\ \nonumber &:=\int_Y (1-e^{-u\tau}e^{s\bar\psi})\, d\mu_{\overline{\phi}} - V(u,s)\\ &=\int_Y (1-e^{-u\tau})\, d\mu_{\overline{\phi}} - \int_Y (1-e^{s\bar\psi})\, d\mu_{\overline{\phi}} +\int_Y (1-e^{-u\tau})(1-e^{s\bar\psi})\, d\mu_{\overline{\phi}} -V(u,s).\end{align} $$

By Lemma 3.1, $V(u,s)\to 0$ , as $u,s\to 0$ and item (i) follows.

(ii) Using (3.7), compute that

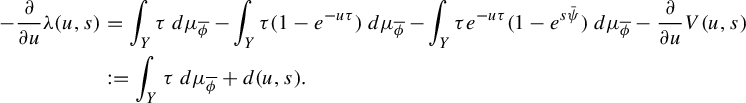$$ \begin{align*} -\frac{\partial}{\partial u}\unicode{x3bb}(u,s)&=\int_Y\kern-1pt\tau\, d\mu_{\overline{\phi}} -\kern-1pt\int_Y \kern-1pt\tau(1-e^{-u\tau})\, d\mu_{\overline{\phi}} -\kern-1pt\int_Y\kern-1pt\tau e^{-u\tau}(1-e^{s\bar\psi})\, d\mu_{\overline{\phi}} -\frac{\partial}{\partial u}V(u,s)\\ &:=\int_Y\tau\, d\mu_{\overline{\phi}} +d(u,s).\end{align*} $$

A calculation similar to that used in obtaining equation (3.5) (via assumptions (GM0) and (GM1)) shows that the functions $\int _Y \tau (1-e^{-u\tau })\, d\mu _{\overline {\phi }}$ and $\int _Y\tau e^{-u\tau }(1-e^{s\bar \psi })\, d\mu _{\overline {\phi }}$ are $C^{q_0-1}$ in u and also that $\int _Y\tau e^{-u\tau }(1-e^{s\bar \psi })\, d\mu _{\overline {\phi }}$ is $C^{q_1}$ in s. Note that

$$ \begin{align*} \frac{\partial}{\partial u}V(u,s)=\int_Y\tau e^{-u\tau}e^{s\bar\psi}(v(0,0)-v(u,s))\, d\mu_{\overline{\phi}} -\int_Y (1-e^{-u\tau}e^{s\bar\psi})\, \frac{\partial}{\partial u}v(u,s))\, d\mu_{\overline{\phi}}. \end{align*} $$

The required smoothness properties of $({\partial }/{\partial u})v(u,s)$ in u and then in s, and as a consequence on $({\partial }/{\partial u})V(u,s)$ , follow from the statement on G in Lemma 3.1(i) and from the statement on K in Lemma 3.1(iii). The statement on the smoothness of $({\partial }/{\partial u})\unicode{x3bb} (u,s)$ in u and s follows by putting all these together. Also, $d(u,0)=-\int _Y \tau (1-e^{-u\tau })\, d\mu _{\overline {\phi }} +O(u)$ and (by, for instance, the dominated convergence theorem applied to $\int _Y \tau (1-e^{-u\tau })\, d\mu _{\overline {\phi }}$ ), we obtain that $d(u,0)\to 0$ as $u\to 0$ .

The statement on the smoothness of $({\partial }/{\partial s})\unicode{x3bb} (u,s)$ in u and s follows by a similar argument.

Item (iii) is an immediate consequence of Lemma 3.1(ii).

We can now proceed to the following proof.

Proof of Proposition 2.4

Throughout, we will use Corollary 3.3 and equation (3.1).

Proof of item (i). Since $\bar p(u,s)=\log \unicode{x3bb} (u,s)$ , using Corollary 3.3(i) and (ii),

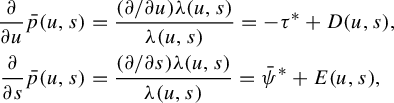(3.8) $$ \begin{align}\begin{aligned} \frac{\partial}{\partial u}\bar p(u,s)&=\frac{({\partial}/{\partial u})\unicode{x3bb}(u,s)}{\unicode{x3bb}(u,s)}=-\tau^*+D(u,s),\\ \frac{\partial}{\partial s}\bar p(u,s)&=\frac{({\partial}/{\partial s})\unicode{x3bb}(u,s)}{\unicode{x3bb}(u,s)} = \bar\psi^*+E(u,s),\end{aligned} \end{align} $$

where:

1. (a) $D(u,s)$ is $C^{q_0-1}$ in u and $C^{q_1}$ in s. Also, $D(u,0)\to 0$ as $u\to 0$ ;

2. (b) $E(u,s)$ is $C^{q_0}$ in u and $C^{q_1-1}$ in s. Also, $E(u,0)\to 0$ as $u\to 0$ .

In particular, $\bar p(0,s)=\unicode{x3bb} (0,s)-1+O(|1-\unicode{x3bb} (0,s)|^2)$ and

(3.9) $$ \begin{align} \frac{\partial}{\partial s}\bar p(0,s)=\frac{({\partial}/{\partial s})\unicode{x3bb}(0,s)}{\unicode{x3bb}(0,s)}=\bar\psi^*+E(0,s), \end{align} $$

where $E(0,s)$ is $C^{q_1-1}$ in s.

For use below in the proof of item (ii), we also note that

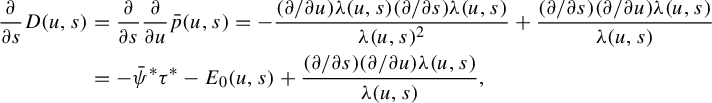(3.10) $$ \begin{align} \frac{\partial}{\partial s} D(u,s)&=\frac{\partial}{\partial s}\frac{\partial}{\partial u}\bar p(u,s) = -\frac{({\partial}/{\partial u})\unicode{x3bb}(u,s)({\partial}/{\partial s})\unicode{x3bb}(u,s)}{\unicode{x3bb}(u,s)^2}+\frac{({\partial}/{\partial s})({\partial}/{\partial u})\unicode{x3bb}(u,s)}{\unicode{x3bb}(u,s)}\nonumber \\ &=-\bar\psi^*\tau^*-E_0(u,s)+\frac{({\partial}/{\partial s})({\partial}/{\partial u})\unicode{x3bb}(u,s)}{\unicode{x3bb}(u,s)}, \end{align} $$

where, using again Corollary 3.3(i) and (ii), $E_0(u,s)$ is $C^{q_0-1}$ in u and $C^{q_1-1}$ in s. Moreover, $\kappa (u,s)=({\partial }/{\partial s})({\partial }/{\partial u})\unicode{x3bb} (u,s)$ satisfies the properties listed in Corollary 3.3(iii). In particular, for all $u\in (0,\delta )$ and $s\in [0,\delta )$ , we have $|\kappa (u,s)|\ll u^{\beta -q_1\gamma -1}$ and $\kappa (u,s)$ is $C^{q_1-1}$ in s. It follows that

(3.11) $$ \begin{align} \frac{\partial}{\partial s} D(u,s)=\frac{\partial}{\partial s}\frac{\partial}{\partial u}\bar p(u,s) =-\bar\psi^*\tau^*-E_1(u,s), \end{align} $$

where $|E_1(u,s)|\ll u^{\beta -q_1\gamma -1}$ and $E_1(u,s)$ is $C^{q_1-1}$ in s.

Proof of item (ii). We proceed via an ‘implicit equation’ exploited in [BTT1, Proof of Theorem 4.1] for the case $\beta <1$ (infinite equilibrium states). The key new ingredient comes down to using the implicit function theorem inside the above mentioned implicit equation.

By item (i), $r(u,s):=({\partial }/{\partial u})\bar p(u,s)$ is well defined. For any small $u_0>0$ ,

(3.12) $$ \begin{align} \bar p(u_0,s)-\bar p(0,s)=\int_0^{u_0} r(u,s)\, du=-\tau^* u_0+ \int_0^{u_0} D(u,s)\, du, \end{align} $$

where $D(u,s)$ is as in item (a) after equation (3.8).

By liftability, for $u_0(s)=p(s)=P_{F}(\phi +s\psi )$ , we obtain $P_T(\overline {\phi +s\psi -u_0})=0$ . Hence, the left-hand side of equation (3.12) is $-P_T(\overline {\phi +s\psi })$ . By assumption, $u_0(s)>0$ for all $s>0$ . The continuity of the pressure function gives that $u_0(s)\to 0$ as $s\to 0$ . Thus, equation (3.12) holds and

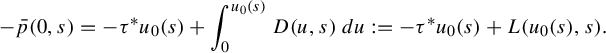(3.13) $$ \begin{align} -\bar p(0,s)=-\tau^* u_0(s)+ \int_0^{u_0(s)} D(u,s)\, du:=-\tau^* u_0(s) +L(u_0(s),s). \end{align} $$

At this point, we can conclude that, as $s\to 0$ ,

(3.14) $$ \begin{align} p(s)=u_0(s)=\frac{\bar p(0,s)}{\tau^*}+\frac{L(u_0(s),s)}{\tau^*}=\frac{\bar p(0,s)}{\tau^*}(1+o(1))=s \frac{\bar\psi^*}{\tau^*}(1+o(1)). \end{align} $$

The first equality is by definition. The second equality follows immediately from equation (3.13), while in the third, we used the smoothness of $D(u,s)$ in s and the fact that $D(u,0)\to 0$ (as in item (a) after equation (3.8)). The fourth equality follows from equation (3.9), since $E(0,s)$ is $C^{q_1-1}$ in s.

We continue with the study of the derivative in s of $u_0(s)$ via equation (3.13). From here on, we write $u_0:=u_0(s)$ .

Since $D(u,s)$ is uniformly continuous in u (since it is $C^{q_0-1}$ in u), $({\partial }/{\partial u_0}) L(u_0,s)=D(u_0,s)$ for all s. Set

$$ \begin{align*} M(u_0,s):=L(u_0,s)+\bar p(0,s), \end{align*} $$

and note that $({\partial }/{\partial u_0}) M(u_0,s)=D(u_0,s)\ne 0$ for all $u_0, s$ small enough. Since $M(u_0,s) - \tau ^* u_0(s) \equiv 0$ and we also know that $|({\partial }/{\partial u_0}) L(u_0,s)|<\infty $ and $|({\partial }/{\partial s}) L(u_0,s)|<\infty $ (because $D(u_0,s)$ is $C^q_1$ in s), the IFT ensures that $u_0(s)$ is differentiable in s and

(3.15) $$ \begin{align} u_0'(s)= \frac{({\partial}/{\partial s}) M(u_0,s)}{\tau^* - ({\partial}/{\partial u_0}) M(u_0,s)}. \end{align} $$

We first estimate the numerator in equation (3.15). Using equation (3.9),

$$ \begin{align*} \frac{\partial}{\partial s} M(u_0,s)=\frac{\partial}{\partial s} L(u_0,s)+\bar\psi^*+E(0,s), \end{align*} $$

where $E(0,s)$ is $C^{q_1-1}$ in s. Using the definition of $L(u_0,s)$ in equation (3.13) and also recalling equation (3.11),

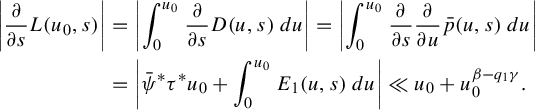(3.16) $$ \begin{align} \bigg|\frac{\partial}{\partial s} L(u_0,s)\bigg|&=\bigg|\kern-2pt\int_0^{u_0}\frac{\partial}{\partial s}D(u,s)\, du\bigg| =\bigg|\kern-2pt\int_0^{u_0}\frac{\partial}{\partial s} \frac{\partial}{\partial u}\bar p(u,s)\, du\bigg|\nonumber \\ &=\bigg|\bar\psi^*\tau^*u_0+\int_0^{u_0}E_1(u,s)\, du\bigg|\ll u_0 +u_0^{\beta-q_1\gamma}. \end{align} $$

Moreover, using the smoothness properties of $E_1$ , we obtain that $({\partial }/{\partial s}) L(u_0,s)$ is $C^{q_1-1}$ in s. Thus,

(3.17) $$ \begin{align} \frac{\partial}{\partial s} M(u_0,s) =\bar\psi^*+\hat E(u_0,s), \end{align} $$

where $\hat E$ is well defined in $u_0$ and $C^{q_1-1}$ in s.

We continue with estimating the denominator in equation (3.15). Recall that $({\partial }/{\partial u_0}) M(u_0,s)=D(u_0,s)$ , where D is as in item (a) after equation (3.8). In particular, $D(u_0,s)$ is $C^{q_1}$ in s. By equation (3.14), $u_0(s)=O(s)$ . Using the smoothness of $D(u_0,s)$ in s, we note that

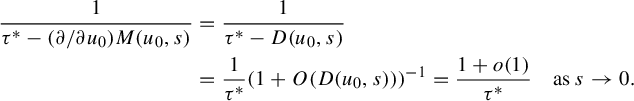$$ \begin{align*} \frac{1}{\tau^*-({\partial}/{\partial u_0}) M(u_0,s)}&=\frac{1}{\tau^* - D(u_0,s)}\\&=\frac{1}{\tau^*}(1+O(D(u_0,s)))^{-1} = \frac{1+o(1)}{\tau^*} \quad \text{as } s\to 0. \end{align*} $$

Recalling the smoothness properties of $\hat E(u_0,s)$ in equation (3.17), we obtain $p'(0)={\bar \psi ^*}/{\tau ^*}$ .

Proof of item (iii). When $q_1>2$ , differentiating in equation (3.14),

$$ \begin{align*} p"(s)=\frac{({\partial^2}/{\partial s^2})\bar p(0,s)}{\tau^*}+\frac{({\partial^2}/{\partial s^2})L(u_0,s)}{\tau^*}. \end{align*} $$

A very lengthy but straightforward calculation based on the smoothness properties of the function $D(u_0,s)$ (after differentiating equation (3.16) once more in s) shows that $({\partial ^2}/{\partial s^2})L(u_0,s)=o(1)$ as $s\to 0$ . (A refined version of this calculation is covered inside the proof of Proposition 2.6. See in particular, equation (5.9), which deals with the case $q_1=\beta /\gamma <2$ . The calculations are the same, just the exponent is different: see Remark 5.2.)

Finally, it is known (see [S1, Theorem 3]) that $({\partial ^2}/{\partial s^2})\bar p(0,s)|_{s=0}=\bar \sigma ^2$ , with $\bar \sigma ^2$ as defined in equation (2.6). Thus, $p"(0)={\bar \sigma ^2}/{\tau ^*}$ , and the conclusion follows from the first equality in equation (2.6).

4 Refined estimates in the setup of Proposition 2.6

We start with a refined version of Lemma 3.1. Recall from equations (3.2) and (3.3) that $H_{[q_1]}(u,s)v=({\partial }/{\partial s^{[q_1]}})R(u,s)v= R(\bar \psi ^{[q_1]} e^{-u\tau } e^{s\bar \psi }v)$ and that $K_{[q_1]}(u,s)v=({\partial }/ {\partial s^{[q_1]}})({\partial }/{\partial u}) R(u,s)v=-R(\bar \psi ^{[q_1]} \tau e^{-u\tau } e^{s\bar \psi }v)$ . In Lemma 3.1, we dealt with the continuity properties of H and K as $u,s\to 0$ . The first result below tells us how the derivatives in s of H and K go to $\infty $ as $u,s\to 0$ .

Lemma 4.1. Assume the setup of Proposition 2.6, in particular, $\gamma \in (\beta -1,\beta )$ . Let $u, s\in [0, \delta _0)$ .

1. (i) If $[q_1]=1$ and $\beta /\gamma \in (1,2]$ , then $\|H_{1}(u,s)\|_{\mathcal {B}_\theta } < \infty $ and $ \|K_{1}(u,0)\|_{\mathcal {B}_\theta }\le C u^{\beta -\gamma -1} $ for some $C>0$ .

   Furthermore, if $\beta /\gamma \in (1,2)$ , there exist $ C_2, C_3, C_4>0$ so that

   $$ \begin{align*} \bigg\|\frac{\partial}{\partial s}H_{1}(u,s)\bigg\|_{\mathcal{B}_\theta}\le C_2 u^{\beta-2\gamma},\quad \bigg\|\frac{\partial}{\partial s}K_{1}(u,s)\bigg\|_{\mathcal{B}_\theta}\le C_3 u^{\beta-2\gamma-1} \end{align*} $$
   and
   $$ \begin{align*} \bigg\|\frac{\partial}{\partial s}H_{1}(0,s)\bigg\|_{\mathcal{B}_\theta}\le C_4 s^{\beta/\gamma-2}. \end{align*} $$

   If $\beta /\gamma =2$ , then there exist $C_2, C_3, C_4>0$ so that

   $$ \begin{align*} \bigg\|\frac{\partial}{\partial s}H_{1}(u,s)\bigg\|_{\mathcal{B}_\theta}\le C_2 \log(1/u),\quad \bigg\|\frac{\partial}{\partial s}K_{1}(u,s)\bigg\|_{\mathcal{B}_\theta}\le C_3 u^{-1} \end{align*} $$
   and
   $$ \begin{align*} \bigg\|\frac{\partial}{\partial s}H_{1}(0,s)\bigg\|_{\mathcal{B}_\theta}\le C_4 \log(1/s). \end{align*} $$

2. (ii) If $[q_1]=2$ and $\beta /\gamma \in (2,3)$ , then $\|H_{2}(u,s)\|_{\mathcal {B}_\theta } < \infty $ and $ \|K_{2}(u,0)\|_{\mathcal {B}_\theta }\le C u^{\beta -2\gamma -1} $ for some $C>0$ . Furthermore, there exist $C_2, C_3, C_4>0$ so that

   $$ \begin{align*} \bigg \|\frac{\partial}{\partial s}H_{2}(u,s)\bigg\|_{\mathcal{B}_\theta}\le C_2 u^{\beta-3\gamma},\quad \bigg\|\frac{\partial}{\partial s}K_{2}(u,s)\bigg\|_{\mathcal{B}_\theta}\le C_3 u^{\beta-3\gamma-1} \end{align*} $$
   and
   $$ \begin{align*} \bigg\|\frac{\partial}{\partial s}H_{2}(0,s)\bigg\|_{\mathcal{B}_\theta}\le C_4 s^{\beta/\gamma-3}. \end{align*} $$

4.1 Some general types of integrals

Before proving Lemma 4.1, we provide estimates of some general types of integrals. These or variants of them will be used throughout the proofs of the technical results in this section. Let $S(x)=\mu _{\overline {\phi }}(\tau <x)$ and recall from assumption (GM1) that $\gamma>\beta -1$ , so $\beta -\gamma <1$ . Since $1-S(x)=c x^{-\beta }(1+o(1))$ ,

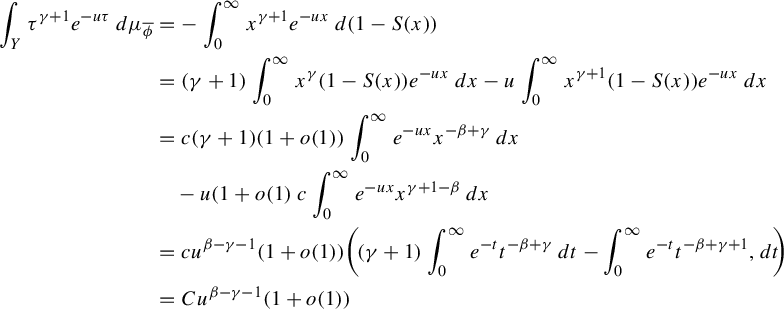(4.1) $$ \begin{align} \nonumber \int_Y \tau^{\gamma+1} e^{-u\tau}\, d\mu_{\overline{\phi}} &=- \int_0^{\infty} x^{\gamma+1} e^{-ux}\, d(1-S(x))\\ \nonumber &=(\gamma+1)\int_0^\infty x^{\gamma}(1-S(x)) e^{-ux}\, dx - u\int_0^\infty x^{\gamma+1}(1-S(x)) e^{-ux}\, d x \\ \nonumber &=c(\gamma+1)(1+o(1))\int_0^\infty e^{-ux} x^{-\beta+\gamma}\, dx\\\nonumber &\quad- u(1+o(1)\, c\int_0^\infty e^{-ux} x^{\gamma+1-\beta}\, d x\\ \nonumber &= c u^{\beta-\gamma-1}(1+o(1)) \bigg(\kern-1pt(\gamma+1) \int_0^\infty e^{-t}t^{-\beta+\gamma} \, d t - \int_0^\infty e^{-t}t^{-\beta+\gamma+1}, d t\!\kern-0.6pt\bigg)\\ & =C u^{\beta-\gamma-1}(1+o(1)) \end{align} $$

for a positive C depending only on $c,\beta ,\gamma $ .

By a similar argument, if $\beta /\gamma \ne 2$ , then

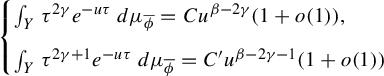(4.2) $$ \begin{align} \begin{cases} \int_Y \tau^{2\gamma} e^{-u\tau}\, d\mu_{\overline{\phi}}= Cu^{\beta-2\gamma}(1+o(1)),\\[2mm] \int_Y \tau^{2\gamma+1} e^{-u\tau}\, d\mu_{\overline{\phi}}= C'u^{\beta-2\gamma-1}(1+o(1)) \end{cases} \end{align} $$

for some $C, C'> 0$ , whereas if $\beta /\gamma =2$ , then

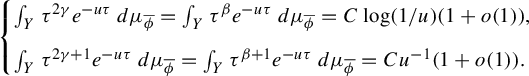(4.3) $$ \begin{align} \begin{cases} \int_Y \tau^{2\gamma} e^{-u\tau}\, d\mu_{\overline{\phi}}= \int_Y \tau^{\beta} e^{-u\tau}\, d\mu_{\overline{\phi}}=C\log(1/u)(1+o(1)),\\[2mm] \int_Y \tau^{2\gamma+1} e^{-u\tau}\, d\mu_{\overline{\phi}}= \int_Y \tau^{\beta+1} e^{-u\tau}\, d\mu_{\overline{\phi}}=Cu^{-1}(1+o(1)). \end{cases} \end{align} $$

Recall that $\bar \psi =C_0-\psi _0=C_0-C_1\tau ^\gamma $ . Similar calculations, this time with $S(x)=\mu _{\overline {\phi }}(\psi _0<x)=\mu _{\overline {\phi }}(C_1\tau ^\gamma <x)$ , show that if $\beta /\gamma <2$ , $\int _Y \psi _0^{2} e^{-s\psi _0}\, d\mu _{\overline {\phi }} =Cs^{\beta /\gamma -2}(1+o(1))$ for some $C>0$ and that if $\beta /\gamma \in (2,3)$ , $\int _Y \psi _0^{3} e^{-s\psi _0}\, d\mu _{\overline {\phi }} =-Cs^{\beta /\gamma -3}(1+o(1))$ for some $C>0$ . The involved constants (denoted by C here) depend only on $c, \beta , \gamma $ . If $\beta /\gamma =2$ , then $ \int _Y \psi _0^{2} e^{-s\psi _0}\, d\mu _{\overline {\phi }} =C\log (1/s)(1+o(1)). $

Next, note that $\bar \psi ^2=C_0^2+\psi _0^2-2C_0\psi _0$ and that $\bar \psi ^3=C_0^3-\psi _0^3+3C_0^2\psi _0-3C_0\psi _0^2$ . Thus, there exist $C_2, C_3, C_4$ depending only on $c, \beta , \gamma $ so that

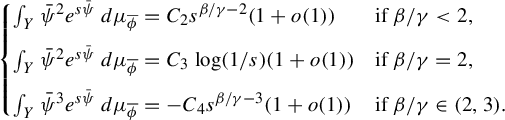(4.4) $$ \begin{align} \begin{cases} \int_Y \bar\psi^{2} e^{s\bar\psi}\, d\mu_{\overline{\phi}} =C_2s^{\beta/\gamma-2}(1+o(1)) & \text{if } \beta/\gamma<2,\\[2mm] \int_Y \bar\psi^{2} e^{s\bar\psi}\, d\mu_{\overline{\phi}} =C_3\log(1/s)(1+o(1)) & \text{if } \beta/\gamma=2,\\[2mm] \int_Y \bar\psi^{3} e^{s\bar\psi}\, d\mu_{\overline{\phi}} =-C_4s^{\beta/\gamma-3}(1+o(1)) & \text{if } \beta/\gamma \in (2,3).\\ \end{cases} \end{align} $$

Proof of Lemma 4.1

We provide the argument for item (i). Item (ii) follows by a similar argument after taking one more derivative in s.

The first estimate on $H_1$ follows directly from Lemma 3.1 with $[q_1]=1$ .

Next, note that if $\beta /\gamma \in (1,2)$ ,

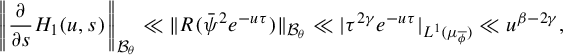$$ \begin{align*} \bigg\|\frac{\partial}{\partial s}H_{1}(u,s)\bigg\|_{\mathcal{B}_\theta}\ll \| R(\bar\psi^{2} e^{-u\tau})\|_{\mathcal{B}_\theta}\ll |\tau^{2\gamma}e^{-u\tau}|_{L^{1}(\mu_{\overline{\phi}})}\ll u^{\beta-2\gamma}, \end{align*} $$

where we used the first equation in equation (4.2). The estimate for the case $\beta /\gamma =2$ follows similarly using equation (4.3). Also, if $\beta /\gamma \in (1,2)$ ,

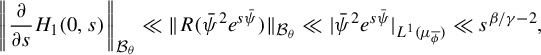$$ \begin{align*} \bigg\|\frac{\partial}{\partial s}H_{1}(0,s)\bigg\|_{\mathcal{B}_\theta}\ll \| R(\bar\psi^{2} e^{s\bar\psi})\|_{\mathcal{B}_\theta}\ll |\bar\psi^{2} e^{s\bar\psi}|_{L^{1}(\mu_{\overline{\phi}})}\ll s^{\beta/\gamma-2}, \end{align*} $$

where we have used the first estimate of equation (4.4) for s. The estimate for the case $\beta /\gamma =2$ follows similarly using the corresponding estimate of equation (4.4) for this case.

Regarding $K_1$ , if $\beta /\gamma \in (1,2)$ ,

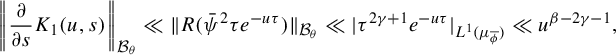$$ \begin{align*} \bigg\|\frac{\partial}{\partial s}K_{1}(u,s)\bigg\|_{\mathcal{B}_\theta}\ll \| R(\bar\psi^{2} \tau e^{-u\tau})\|_{\mathcal{B}_\theta}\ll |\tau^{2\gamma+1}e^{-u\tau}|_{L^{1}(\mu_{\overline{\phi}})}\ll u^{\beta-2\gamma-1}, \end{align*} $$

where we used the second equation in equation (4.2). The estimate for the case $\beta /\gamma =2$ follows similarly using the corresponding estimates for this case.

We shall also need the following refined version of Corollary 3.3(ii) and (iii). Item (i) of Corollary 3.3 remains unchanged. Again, the derivatives in s of several quantities in the lemma below blow up as $u,s\to 0$ but in a controlled way.

We recall that in the setup of Proposition 2.6, $\gamma <1$ and $\beta <2$ .

Lemma 4.2. The following hold in the setup of Proposition 2.6. Let $u, s\in [0,\delta _0)$ .

1. (i) $({\partial }/{\partial u})\unicode{x3bb} (u,s)=-\tau ^*+d(u,s)$ , where $d(u,s)$ is as follows.

   There exists $C>0$ depending only on $c,\beta $ so that $d(u,0)= Cu^{\beta -1}(1+o(1))$ . Moreover, there exist $C_2, C_3>0$ depending only on $c,\beta , \gamma $ so that as $u,s\to 0$ ,

   $$ \begin{align*} \frac{\partial}{\partial s} d(u,s)= C_2 u^{\beta-\gamma-1}(1+o(1)) &\text{ if }\beta/\gamma\in (1,2], \end{align*} $$
   $$ \begin{align*} \frac{\partial^2}{\partial s^2} d(u,s)= C_3 u^{\beta-\gamma-2}(1+o(1)) &\text{ if }\beta/\gamma\in (2,3). \end{align*} $$

2. (ii) The following holds for some $C, C'>0$ depending only on $c,\beta /\gamma $ :

   $$ \begin{align*} \frac{\partial}{\partial s}\unicode{x3bb}(u,s)=\bar\psi^*+ e(u,s) \,{+} \begin{cases} h(s)+ h_0(s) &\text{if }\beta/\gamma\kern1.3pt{\in}\kern1.3pt (1,2],\\ -s\int_Y \bar\psi^2\, d\mu_{\overline{\phi}}\kern1.3pt{+}\kern1.3pt Cs^{\beta/\gamma-1}\kern1.3pt{+}\kern1.3pt h_1(s) &\text{if }\beta/\gamma\kern1.3pt{\in}\kern1.3pt (2,3), \end{cases} \end{align*} $$
   where $h(s)=Cs^{\beta /\gamma -1}$ if $\beta /\gamma \in (1,2)$ , $h(s)=C\log (1/s)$ if $\beta /\gamma =2$ and where $h_0$ , $h_1$ and e are as follows:

   1. (a) $h_0(s)=o(s^{\beta /\gamma -1})$ , $h^{\prime }_0(s)\kern1.3pt{=}\kern1.3pt o(s^{\beta /\gamma -2})$ if $\beta /\gamma \kern1.3pt{\in}\kern1.3pt (1,2)$ and $h^{\prime }_0(s)\kern1.3pt{=}\kern1.3pt o(\log (1/s))$ if $\beta /\gamma =2$ ;

   2. (b) $h_1(s)=o(s^{\beta /\gamma -1})$ , $h^{\prime }_1(s)=C' s^{\beta /\gamma -2}(1+o(1))$ and $h^{\prime \prime }_1(s)=C' s^{\beta /\gamma -3}(1+o(1))$ ;

   3. (c) $e(0,s)=O(s)$ , $e(u,0)=o(1)$ as $u,s\to 0$ and:

      1. (*) if $\beta /\gamma \in (1,2)$ , then $({\partial }/{\partial s}) e(u,s)= o(u^{\beta -\gamma -1})+o(s^{\beta /\gamma -2})$ . Also, $({\partial }/{\partial s}) e(0,s)=o(s^{\beta /\gamma -2})$ ;

      2. (**) if $\beta /\gamma =2$ , then $({\partial }/{\partial s}) e(u,s)= o(u^{\beta -\gamma -1})+o(\log (1/s))$ . Also, $({\partial }/{\partial s}) e(0,s)=o(\log (1/s))$ ;

      3. (***) if $\beta /\gamma \in (2,3)$ , then $({\partial }/{\partial s}) e(u,s)= o(u^{\beta -\gamma -2})+o(s^{\beta /\gamma -3})$ . Also, $({\partial }/{\partial s}) e(0,s)= o(s^{\beta /\gamma -3})$ .

3. (iii) Let $\kappa (u,s)=({\partial }/{\partial s})({\partial }/{\partial u})\unicode{x3bb} (u,s)$ . Then, there exist $C, C'>0$ depending only on $c,\beta ,\gamma $ , so that

   $$ \begin{align*} \begin{cases} \kappa(u,0)=C u^{\beta-\gamma-1} + O(u^{\beta-\gamma-1+{\epsilon}_0}) & \text{if } \beta/\gamma\in (1,2], \\ ({\partial}/{\partial s})\kappa(u,s)|_{s=0}=C' u^{\beta-2\gamma-1} + O(u^{\beta-2\gamma-1+{\epsilon}_0}) & \text{if } \beta/\gamma\in (2,3), \end{cases} \end{align*} $$
   as $u\to 0$ and for any ${\epsilon }_0>0$ .

   Also, the following hold for some $\hat C_2, \hat C_3>0$ depending only on $c,\beta ,\gamma $ , as $u, s\to 0$ :

   1. (*) if $\beta /\gamma \in (1,2]$ , then $({\partial }/{\partial s})\kappa (u,s)=\hat C_2 u^{\beta -2\gamma -1}(1+o(1))$ ;

   2. (**) if $\beta /\gamma \in (2,3)$ , then $({\partial ^2}/{\partial s^2})\kappa (u,s)=-\hat C_3 u^{\beta -3\gamma -1}(1+o(1))$ .

Proof of Lemma 4.2

We continue from the proof of Corollary 3.3(ii) with the same notation.

Proof of item (i). Recall that

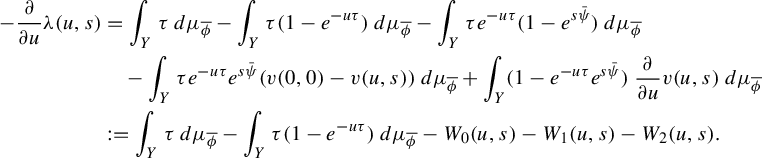(4.5) $$ \begin{align} \nonumber -\frac{\partial}{\partial u}\unicode{x3bb}(u,s)&=\int_Y\tau\, d\mu_{\overline{\phi}} -\int_Y \tau(1-e^{-u\tau})\, d\mu_{\overline{\phi}} -\int_Y\tau e^{-u\tau}(1-e^{s\bar\psi})\, d\mu_{\overline{\phi}} \\ \nonumber &\quad -\int_Y\tau e^{-u\tau}e^{s\bar\psi}(v(0,0)-v(u,s))\, d\mu_{\overline{\phi}}+\int_Y (1-e^{-u\tau}e^{s\bar\psi})\, \frac{\partial}{\partial u}v(u,s)\, d\mu_{\overline{\phi}}\\ &:=\int_Y\tau\, d\mu_{\overline{\phi}} -\int_Y \tau(1-e^{-u\tau})\, d\mu_{\overline{\phi}} -W_0(u,s) -W_1(u,s)-W_2(u,s).\end{align} $$

Recall $\mu _{\overline \phi }(\tau \ge x)=c x^{-\beta }(1+o(1))$ . A standard calculation (mostly similar to that used in obtaining equation (4.1)) shows that there exists $C>0$ depending on c and $\beta $ so that

$$ \begin{align*} - \int_Y \tau(1-e^{-u\tau})\, d\mu_{\overline{\phi}}= Cu^{\beta-1}(1+o(1)). \end{align*} $$

Set $d(u,s)= \int _Y \tau (1-e^{-u\tau })\, d\mu _{\overline {\phi }} -W_0(u,s) -W_1(u,s)-W_2(u,s)$ with $W_0, W_1, W_2$ as defined in equation (4.5). Note that $W_0(u,0)=0$ , $|W_1(u,0)|\ll u$ and $|W_2(u,0)|\ll u$ , and that so far, we obtained the expression for $d(u,0)$ .

Note that $({\partial }/{\partial s})d(u,s)=-({\partial }/{\partial s}) (W_0(u,s) +W_1(u,s)+W_2(u,s))$ . We continue with the derivatives in s of $W_0, W_1, W_2$ by considering each of the two cases.

The term $\mathit {W_0(u,s)}$ . First, $({\partial }/{\partial s})W_0(u,s) =\int _Y\tau \bar \psi e^{-u\tau }e^{s\bar \psi }\, d\mu _{\overline {\phi }} =\int _Y\tau \bar \psi e^{-u\tau }\, d\mu _{\overline {\phi }}+ \int _Y\tau \bar \psi e^{-u\tau } (e^{s\bar \psi }-1)\, d\mu _{\overline {\phi }}$ .

If $\mathit {\beta /\gamma \in (1,2]}$ , then $\beta -\gamma \in (0,1)$ . Since $\bar \psi =C_0-C_1\tau ^\gamma $ ,

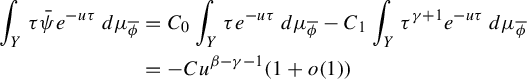(4.6) $$ \begin{align} \int_Y\tau \bar\psi e^{-u\tau}\, d\mu_{\overline{\phi}}&=C_0\int_Y\tau e^{-u\tau}\, d\mu_{\overline{\phi}} -C_1\int_Y \tau^{\gamma+1} e^{-u\tau}\, d\mu_{\overline{\phi}} \nonumber \\ &=-C u^{\beta-\gamma-1}(1+o(1)) \end{align} $$

for some $C>0$ depending on c and $\beta , \gamma $ . In the last equality, we have used that equation (4.1) holds as soon as $\beta -\gamma \in (0,1)$ . Since we also know that $e^{s\bar \psi }-1\to 0$ as $s\to 0$ , the dominated convergence theorem implies that $\int _Y\tau \bar \psi e^{-u\tau } (e^{s\bar \psi }-1)\, d\mu _{\overline {\phi }}=o(u^{\beta -\gamma -1})$ . So, if $\beta /\gamma \in (1,2]$ , then $({\partial }/{\partial s})W_0(u,s) =-C u^{\beta -\gamma -1}(1+o(1))$ .

If $\mathit {\beta /\gamma \in (2,3)}$ , then $\beta -2\gamma <\gamma <1$ and $\beta -2\gamma \in (0,\gamma )\subset (0,1)$ . Note that $({\partial ^2}/{\partial s^2})W_0(u,s) =\int _Y\tau \bar \psi ^2 e^{-u\tau }e^{s\bar \psi }\, d\mu _{\overline {\phi }}$ . Proceeding similarly to the argument above in the case $\beta /\gamma \in (1,2]$ , we compute that if $\beta -2\gamma \in (0,1)$ , then $({\partial ^2}/{\partial s^2})W_0(u,s)=C u^{\beta -2\gamma -1}(1+o(1))$ for some C depending on c and $\beta , \gamma $ , where we use an analogue of equation (4.1) for the case $\beta -2\gamma \in (0,1)$ . So, if $\beta /\gamma \in (2,3)$ , then $({\partial }/{\partial s})W_0(u,s) =-C u^{\beta -2\gamma -1}(1+o(1))$ .

The term $\mathit {W_1(u,s)}$ . Start from

$$ \begin{align*} \frac{\partial}{\partial s}W_1(u,s)=\int_Y\tau\bar\psi e^{-u\tau}e^{s\bar\psi}(v(u,0)-v(u,s))\, d\mu_{\overline{\phi}}-\int_Y\tau e^{-u\tau}e^{s\bar\psi}\, \frac{\partial}{\partial s}v(u,s)\, d\mu_{\overline{\phi}}. \end{align*} $$

Recall that if $\mathit {\beta /\gamma \in (1,2]}$ , then $\beta -\gamma \in (0,1)$ . Since

$$ \begin{align*} \|v(0,0)-v(u,s)\|_{\mathcal{B}_\theta}\le \|v(0,s)-v(u,s)\|_{\mathcal{B}_\theta} +\|v(u,0)-v(u,s)\|_{\mathcal{B}_\theta}\le u+s, \end{align*} $$

using equation (4.6), we obtain $\int _Y\tau \bar \psi e^{-u\tau }e^{s\bar \psi }(v(u,0)-v(u,s))\, d\mu _{\overline {\phi }}=o(u^{\beta -\gamma -1})$ , as $u,s\to 0$ . Also, by Lemma 4.1(i) (statement on $H_1$ ), $\|({\partial }/{\partial s})v(u,s)\|_{\mathcal {B}_\theta }<\infty $ . Recall $e^{s\bar \psi }\ll e^{sC_0}e^{-s\tau ^\gamma }$ . Thus,

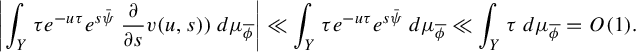$$ \begin{align*} \bigg|\kern-2pt\int_Y\tau e^{-u\tau}e^{s\bar\psi}\, \frac{\partial}{\partial s}v(u,s))\, d\mu_{\overline{\phi}}\bigg|\ll \int_Y\tau e^{-u\tau}e^{s\bar\psi}\, d\mu_{\overline{\phi}}\ll \int_Y\tau\, d\mu_{\overline{\phi}} =O(1). \end{align*} $$

Thus, if $\beta /\gamma \in (1,2]$ , $({\partial }/{\partial s})W_1(u,s)= o(u^{\beta -\gamma -1})$ , as $u,s\to 0$ .

Next, recall that if $\mathit {\beta /\gamma \in (2,3)}$ , then $\beta -2\gamma \in (0,1)$ . In this case, taking one more derivative,

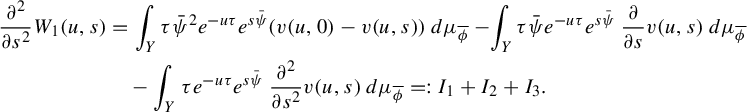$$ \begin{align*} \frac{\partial^2}{\partial s^2}W_1(u,s)& =\int_Y\kern-1.1pt\tau\bar\psi^2 e^{-u\tau}e^{s\bar\psi}(v(u,0)-v(u,s))\, d\mu_{\overline{\phi}} \,{-}\!\int_Y\kern-1pt\tau\bar\psi e^{-u\tau}e^{s\bar\psi}\, \frac{\partial}{\partial s}v(u,s)\, d\mu_{\overline{\phi}}\\ &\quad-\int_Y\tau e^{-u\tau}e^{s\bar\psi}\, \frac{\partial^2}{\partial s^2}v(u,s)\, d\mu_{\overline{\phi}}=:I_1+I_2+I_3.\end{align*} $$

Using the analogue of equation (4.6) for the case $\beta -2\gamma \in (0,1)$ ,

$$ \begin{align*} |I_1|\ll \|v(0,0)-v(u,s)\|_{\mathcal{B}_\theta} \int_Y\tau\bar\psi^2 e^{-u\tau}\, d\mu_{\overline{\phi}} \ll u^{\beta-2\gamma-1} (u+s)=o(u^{\beta-2\gamma-1}) \end{align*} $$

as $u,s\to 0$ .

Next, we already know that $\|({\partial }/{\partial s})v(u,s)\|_{\mathcal {B}_\theta }<\infty $ . Thus, $|I_2|\ll \int _Y\tau ^{\gamma +1} e^{-u\tau } e^{s\bar \psi } d\mu _{\overline {\phi }}\kern1.2pt{\ll}\kern1.2pt u^{\beta -\gamma -1}$ . Also, by Lemma 4.1(ii) (the statement on $H_2$ ), $\|({\partial ^2}/{\partial s^2})v(u,s))\|_{\mathcal {B}_\theta }{<}\infty $ and thus, $|I_3|\ll \int _Y\tau e^{-u\tau }e^{s\bar \psi }\, d\mu _{\overline {\phi }}=O(1)$ . Thus, if $\beta /\gamma \in (2,3)$ , then $({\partial }/{\partial s}) W_1(u,s)= o(u^{\beta -2\gamma -1})$ , as $u,s\to 0$ .

The term $\mathit {W_2(u,s)}$ . Note that

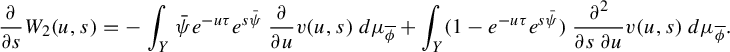$$ \begin{align*} \frac{\partial}{\partial s}W_2(u,s)=-\int_Y \bar\psi e^{-u\tau}e^{s\bar\psi}\, \frac{\partial}{\partial u}v(u,s)\, d\mu_{\overline{\phi}} +\int_Y (1-e^{-u\tau}e^{s\bar\psi})\, \frac{\partial^2}{ \partial s\,\partial u}v(u,s)\, d\mu_{\overline{\phi}}. \end{align*} $$

If $\mathit {\beta /\gamma \in (1,2]}$ , by Lemma 3.1 (statement on $G_{[q_0]}$ with $[q_0]=1$ ), $\|({\partial }/{\partial u})v(u,s)\|_{\mathcal {B}_\theta } <\infty $ . Recall $e^{s\bar \psi }\ll e^{sC_0}e^{-s\tau ^\gamma }$ . Thus, $|\int _Y \bar \psi e^{-u\tau }e^{s\bar \psi }\, ({\partial }/{\partial u})v(u,s)\, d\mu _{\overline {\phi }}|\ll \int _Y \bar \psi \, ({\partial }/{\partial u}) v(u,s)\, d\mu _{\overline {\phi }}=O(1)$ . By Lemma 4.1(i) (statement on $K_1$ ), $\|({\partial ^2}/{\partial s\, \partial u})v(u,s)\|_{\mathcal {B}_\theta }\ll u^{\beta -\gamma -1}$ . So, $|\int _Y (1-e^{-u\tau }e^{s\bar \psi })\, ({\partial ^2}/{ \partial s\,\partial u}) v(u,s)\, d\mu _{\overline {\phi }}|\ll u^{\beta -\gamma -1}\int _Y (1- e^{-u\tau }e^{s\bar \psi }) d\mu _{\overline {\phi }}=o(u^{\beta -\gamma -1})$ , as $u,s\to 0$ . Thus, if $\beta /\gamma \in (1,2]$ , $({\partial }/{\partial s})W_2(u,s)= o(u^{\beta -\gamma -1})$ , as $u,s\to 0$ .

If $\mathit {\beta /\gamma \in (2,3)}$ , then we differentiate once more,

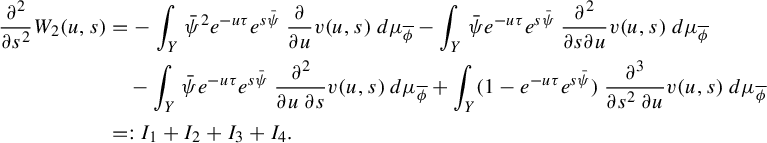$$ \begin{align*} \frac{\partial^2}{\partial s^2}W_2(u,s)& =-\int_Y \bar\psi^2 e^{-u\tau}e^{s\bar\psi}\, \frac{\partial}{\partial u}v(u,s)\, d\mu_{\overline{\phi}} -\int_Y \bar\psi e^{-u\tau}e^{s\bar\psi}\, \frac{\partial^2}{\partial s\partial u}v(u,s)\, d\mu_{\overline{\phi}}\\ &\quad-\int_Y \bar\psi e^{-u\tau}e^{s\bar\psi}\, \frac{\partial^2}{\partial u\, \partial s}v(u,s)\, d\mu_{\overline{\phi}}+\int_Y (1-e^{-u\tau}e^{s\bar\psi})\, \frac{\partial^3}{ \partial s^2\,\partial u}v(u,s)\, d\mu_{\overline{\phi}}\\ &=:I_1+I_2+I_3+I_4. \end{align*} $$

Since $\bar \psi \in L^2$ for $\beta /\gamma \in (2,3)$ , and since $\|({\partial }/{\partial u})v(u,s)\|_{\mathcal {B}_\theta }<\infty $ , $|I_1|= O(1)$ . Also, it is easy to see that $|I_2|= O(1)$ and $|I_3|= O(1)$ . For $I_4$ , we note that by Lemma 4.1(ii) (statement on $K_2$ ), $\|({\partial ^3}/{ \partial s^2\,\partial u})v(u,s)\|_{\mathcal {B}_\theta }\ll u^{\beta -2\gamma -1}$ . Thus, $|I_4|=o(u^{\beta -2\gamma -1})$ , as $u,s\to 0$ . So, if $\beta /\gamma \in (2,3)$ , then $({\partial ^2}/{\partial s^2})W_2(u,s)= o(u^{\beta -2\gamma -1})$ , as $u,s\to 0$ .

The statements on $({\partial }/{\partial s})\,d(u,s)$ for $\beta /\gamma \in (1,2]$ and on $({\partial ^2}/{\partial s^2})\,d(u,s)$ for $\beta /\gamma \in (2,3)$ follow by putting all the above estimates on $W_0, W_1, W_2$ together.

Proof of item (ii). Recalling equation (3.7) and differentiating in s,

$$ \begin{align*} \frac{\partial}{\partial s}\unicode{x3bb}(u,s) =\int_Y\bar\psi\, d\mu_{\overline{\phi}} + \int_Y \bar\psi(e^{s\bar\psi}-1)\, d\mu_{\overline{\phi}} + e(u,s) \end{align*} $$

for

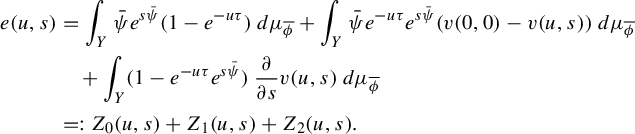(4.7) $$ \begin{align} e(u,s) & = \int_Y \bar\psi e^{s\bar\psi}(1- e^{-u\tau})\, d\mu_{\overline{\phi}} \nonumber+\int_Y\bar\psi e^{-u\tau}e^{s\bar\psi}(v(0,0)-v(u,s))\, d\mu_{\overline{\phi}} \nonumber \\ \nonumber &\quad +\int_Y (1-e^{-u\tau}e^{s\bar\psi})\, \frac{\partial}{\partial s}v(u,s)\, d\mu_{\overline{\phi}}\\ &=:Z_0(u,s)+Z_1(u,s)+Z_2(u,s). \end{align} $$

A standard calculation (already used in showing equation (4.1)) shows that, given that $\bar \psi =C_0-C_1\tau ^\gamma $ and that $\mu _Y(\tau \ge x)=c x^{-\beta }(1+o(1))$ , there exists $C, C'>0$ depending on c and $\beta /\gamma $ so that

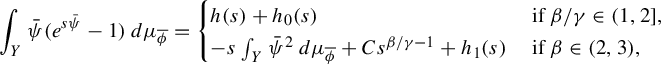(4.8) $$ \begin{align} \int_Y \bar\psi(e^{s\bar\psi}-1)\, d\mu_{\overline{\phi}} = \begin{cases} h(s)+ h_0(s) &\text{ if }\beta/\gamma\in (1,2],\\ -s\int_Y \bar\psi^2\, d\mu_{\overline{\phi}}+ Cs^{\beta/\gamma-1}+h_1(s) &\text{ if }\beta\in (2,3), \end{cases} \end{align} $$

where $h(s)=Cs^{\beta /\gamma -1}$ if $\beta /\gamma \in (1,2)$ , $h(s)=C\log (1/s)$ if $\beta /\gamma =2$ , and where $h_0$ and $h_1$ are as follows: (a) $h_0(s)=o(s^{\beta /\gamma -1})$ , $h^{\prime }_0(s)=o(s^{\beta /\gamma -2})$ if $\beta /\gamma \in (1,2)$ and $h^{\prime }_0(s)=o(\log (1/s))$ if $\beta /\gamma =2$ ; (b) $h_1(s)=o(s^{\beta /\gamma -1})$ , $h^{\prime }_1(s)=C' s^{\beta /\gamma -2}(1+o(1))$ and $h^{\prime \prime }_1(s)=C' s^{\beta /\gamma -3}(1+o(1))$ .

We continue with the study of $e(u,s)$ . It is easy to see from equation (4.7) with $u=0$ and $s=0$ , respectively, that $|e(0,s)|=O(s)$ as $s\to 0$ and that $|e(u,0)|=o(1)$ as $u\to 0$ ; to show $|e(u,0)|=o(1)$ , we also use the dominated convergence theorem. Also, it is easy to see that if $\beta /\gamma \in (1,2]$ , then

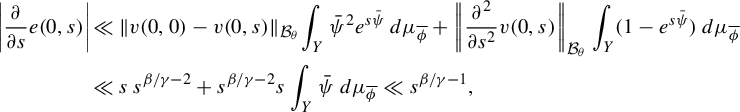$$ \begin{align*} \bigg|\frac{\partial}{\partial s}e(0,s)\bigg|\kern-2pt&\ll \|v(0,0)-v(0,s) \|_{\mathcal{B}_\theta} \kern-2pt\int_Y\bar\psi^2 e^{s\bar\psi}\, d\mu_{\overline{\phi}} +\bigg\|\frac{\partial^2}{\partial s^2}v(0,s)\bigg\|_{\mathcal{B}_\theta}\int_Y (1-e^{s\bar\psi})\, d\mu_{\overline{\phi}}\\ &\ll s\, s^{\beta/\gamma-2} +s^{\beta/\gamma-2} s \int_Y \bar\psi\, d\mu_{\overline{\phi}}\ll s^{\beta/\gamma-1}, \end{align*} $$

where in the previous to last inequality, we have used Lemma 4.1(i) (statement on $({\partial }/{\partial s})H_1(0,s)$ ) and the estimate in s in equation (4.4). If $\beta /\gamma = 2$ , then, again by Lemma 4.1(i), the same statement holds with $s^{\beta /\gamma -2}$ replaced by $\log 1/s$ . In this case, $|({\partial }/{\partial s})e(0,s)|$ is bounded by $s \log 1/s$ .

We continue with the derivatives of $Z_0, Z_1, Z_2$ in equation (4.7), when $u\ne 0$ , by considering each of the two cases.

The term $\mathit {Z_0(u,s)}$ . Differentiating in s, we obtain

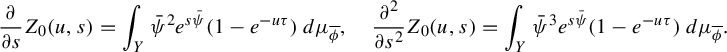$$ \begin{align*} \frac{\partial}{\partial s} Z_0(u,s) =\int_Y \bar\psi^2 e^{s\bar\psi}(1- e^{-u\tau})\, d\mu_{\overline{\phi}}, \quad \frac{\partial^2}{\partial s^2} Z_0(u,s) =\int_Y \bar\psi^3 e^{s\bar\psi}(1- e^{-u\tau})\, d\mu_{\overline{\phi}}. \end{align*} $$

Using the estimates in equation (4.4) in s in equation (4.4), as $s\to 0$ , $\int _Y \bar \psi ^2 e^{s\bar \psi }\, d\mu _{\overline {\phi }}=Cs^{\beta /\gamma -2}(1+o(1))$ if $\beta /\gamma \in (1,2)$ , $\int _Y \bar \psi ^2 e^{s\bar \psi }\, d\mu _{\overline {\phi }}=C\log (1/s)(1+o(1))$ if $\beta /\gamma =2$ and $\int _Y \bar \psi ^3 e^{s\bar \psi }\, d\mu _{\overline {\phi }}=Cs^{\beta /\gamma -3}(1+o(1))$ if $\beta /\gamma \in (2,3)$ for some $C>0$ (varying from estimate to estimate).

Thus, as $u,s\to 0$ , $({\partial }/{\partial s}) Z_0(u,s)=o(s^{\beta /\gamma -2})$ if $\mathit {\beta /\gamma \in (1,2)}$ , $({\partial }/{\partial s}) Z_0(u,s)=o(\log (1/s))$ if $\mathit {\beta /\gamma =2}$ and $({\partial ^2}/{\partial s^2}) Z_0(u,s)=o(s^{\beta /\gamma -3})$ if $\mathit {\beta /\gamma \in (2,3)}$ .

The term $\mathit {Z_1(u,s)}$ . Differentiating in s, we obtain

$$ \begin{align*} \frac{\partial}{\partial s} Z_1(u,s) =\int_Y\bar\psi^2 e^{-u\tau}e^{s\bar\psi}(v(0,0)-v(u,s))\, d\mu_{\overline{\phi}} -\int_Y\bar\psi e^{-u\tau}e^{s\bar\psi}\, \frac{\partial}{\partial s} v(u,s)\, d\mu_{\overline{\phi}}. \end{align*} $$

Recall that $\|v(0,0)-v(u,s)\|_{\mathcal {B}_\theta }\ll u+s$ . Thus, if $\mathit {\beta /\gamma \in (1,2)}$ ,

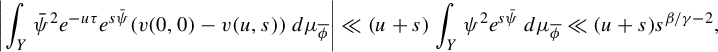$$ \begin{align*} \bigg|\kern-2pt\int_Y\bar\psi^2 e^{-u\tau}e^{s\bar\psi}(v(0,0)-v(u,s))\, d\mu_{\overline{\phi}} \bigg|\ll (u+s)\int_Y\psi^2 e^{s\bar\psi}\, d\mu_{\overline{\phi}}\ll (u+s)s^{\beta/\gamma-2}, \end{align*} $$

where we have used that $\int _Y \bar \psi ^2 e^{s\bar \psi }\, d\mu _{\overline {\phi }}=Cs^{\beta /\gamma -2}(1+o(1))$ .

Recall that by Lemma 4.1(i) (statement on $H_1$ ), $\|({\partial }/{\partial s})v(u,s)\|_{\mathcal {B}_\theta }<\infty $ . Thus, $|\kern -2pt\int _Y\bar \psi e^{-u\tau }e^{s\bar \psi }\, ({\partial }/{\partial s}) v(u,s))\, d\mu _{\overline {\phi }}|=O(1)$ . Therefore, we have the following.

If $\mathit {\beta /\gamma \in (1,2)}$ , then $({\partial }/{\partial s})Z_1(u,s)= O((u +s)s^{\beta /\gamma -2})$ .

If $\mathit {\beta /\gamma =2}$ , then we proceed the same way using $\int _Y \bar \psi ^2 e^{s\bar \psi }\, d\mu _{\overline {\phi }}=C\log (1/s) (1+o(1))$ , which gives $({\partial }/{\partial s})Z_1(u,s)= O((u+s) \log (1/s))$ .

If $\mathit {\beta /\gamma \in (2,3)}$ , differentiating once more in s and using a similar argument to the case $\beta /\gamma \in (1,2)$ above (exploiting that $\int _Y \bar \psi ^3 e^{s\bar \psi }\, d\mu _{\overline {\phi }}=Cs^{\beta /\gamma -3}(1+o(1))$ ), we obtain $({\partial ^2}/{\partial s^2})Z_1(u,s)= O((u+s) s^{\beta /\gamma -3})$ .

The term $\mathit {Z_2(u,s)}$ . Differentiating in s,

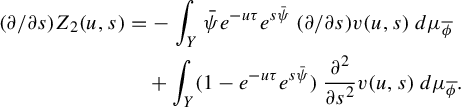$$ \begin{align*} ({\partial}/{\partial s}) Z_2(u,s)&=-\int_Y \bar\psi e^{-u\tau}e^{s\bar\psi}\, ({\partial}/{\partial s})v(u,s)\, d\mu_{\overline{\phi}}\\ &\quad +\int_Y (1-e^{-u\tau}e^{s\bar\psi})\, \frac{\partial^2}{\partial s^2}v(u,s)\, d\mu_{\overline{\phi}}. \end{align*} $$

We already know that $\|({\partial }/{\partial s})v(u,s)\|_{\mathcal {B}_\theta }<\infty $ . Hence, $|\kern -2pt\int _Y \bar \psi e^{-u\tau }e^{s\bar \psi }\, ({\partial }/{\partial s})v(u,s) d\mu _{\overline {\phi }} |=O(1)$ . Also, if $\mathit {\beta /\gamma \in (1,2]}$ , by Lemma 4.1(i) (statement on $H_1$ ), $\|({\partial ^2}/{\partial s^2}) v(u,s)\|_{\mathcal {B}_\theta }\ll u^{\beta -\gamma -1}$ . Thus, $|\kern -2pt\int _Y (1-e^{-u\tau }e^{s\bar \psi })\, ({\partial ^2}/{\partial s^2})v(u,s)\, d\mu _{\overline {\phi }} |=o(u^{\beta -\gamma -1})$ , as $u,s\to 0$ . Thus, if $\beta /\gamma \in (1,2]$ , then $({\partial }/{\partial s})Z_2(u,s)=o(u^{\beta -\gamma -1})$ , as $u,s\to 0$ .

If $\mathit {\beta /\gamma \in (2,3)}$ , differentiating once more in s and using a similar argument to the case $\beta /\gamma \in (1,2]$ above (but using the statement on $H_2$ in Lemma 4.1(ii)), we obtain $({\partial ^2}/{\partial s^2})Z_2(u,s)= o(u^{\beta -2\gamma -1})$ , as $u,s\to 0$ .

The statement on $({\partial }/{\partial s}) e(u,s)$ for $\beta /\gamma \in (1,2]$ and for $({\partial ^2}/{\partial s^2}) e(u,s)$ for $\beta /\gamma \in (2,3)$ follows by putting all the above estimates on $Z_0, Z_1, Z_2$ together.

Proof of item (iii). We continue from equation (4.5) and compute that

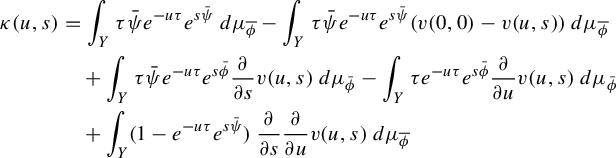$$ \begin{align*} \kappa(u,s)&=\int_Y\tau \bar\psi e^{-u\tau}e^{s\bar\psi}\, d\mu_{\overline{\phi}} -\int_Y\tau\bar\psi e^{-u\tau}e^{s\bar\psi}(v(0,0)-v(u,s))\, d\mu_{\overline{\phi}}\\ &\quad +\int_Y \tau \bar\psi e^{-u\tau} e^{s\bar\phi} \frac{\partial}{\partial s} v(u,s) \, d\mu_{\bar\phi} - \int_Y \tau e^{-u\tau} e^{s\bar\phi} \frac{\partial}{\partial u} v(u,s) \, d\mu_{\bar\phi} \\ &\quad +\int_Y (1-e^{-u\tau}e^{s\bar\psi})\, \frac{\partial}{\partial s}\frac{\partial}{\partial u}v(u,s)\, d\mu_{\overline{\phi}} \end{align*} $$

and

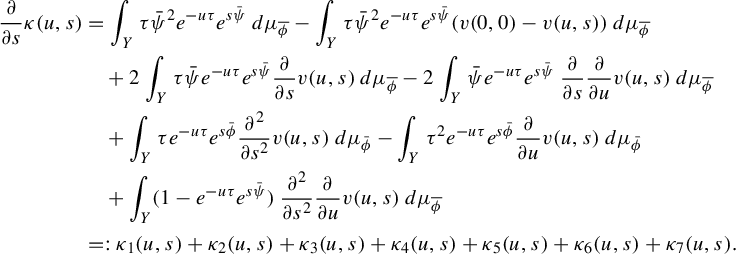(4.9) $$ \begin{align} \nonumber \frac{\partial}{\partial s}\kappa(u,s)&=\int_Y\tau \bar\psi^2 e^{-u\tau}e^{s\bar\psi}\, d\mu_{\overline{\phi}} -\int_Y\tau\bar\psi^2 e^{-u\tau}e^{s\bar\psi}(v(0,0)-v(u,s))\, d\mu_{\overline{\phi}}\\ \nonumber & \quad + 2\int_Y\tau\bar\psi e^{-u\tau}e^{s\bar\psi}\frac{\partial}{\partial s}v(u,s)\, d\mu_{\overline{\phi}} - 2\int_Y \bar\psi e^{-u\tau}e^{s\bar\psi}\, \frac{\partial}{\partial s}\nonumber \frac{\partial}{\partial u}v(u,s)\, d\mu_{\overline{\phi}}\\ \nonumber & \quad + \int_Y \tau e^{-u\tau} e^{s\bar\phi} \frac{\partial^2}{\partial s^2} v(u,s) \, d\mu_{\bar\phi} - \int_Y \tau^2 e^{-u\tau} e^{s\bar\phi} \frac{\partial}{\partial u} v(u,s) \, d\mu_{\bar\phi} \\ \nonumber & \quad +\int_Y (1-e^{-u\tau}e^{s\bar\psi})\, \frac{\partial^2}{\partial s^2}\frac{\partial}{\partial u}v(u,s)\, d\mu_{\overline{\phi}}\\ & =:\kappa_1(u,s)+\kappa_2(u,s)+\kappa_3(u,s) +\kappa_4(u,s) +\kappa_5(u,s) +\kappa_6(u,s) +\kappa_7(u,s). \end{align} $$

We provide the argument for the case $\beta /\gamma \in (1,2]$ . The case $\beta /\gamma \in (2,3)$ follows by a similar argument after differentiating equation (4.9) once more in s.

Using Lemma 4.1(i),

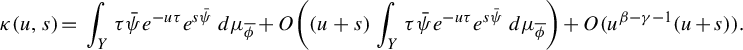$$ \begin{align*} \kappa(u,s)\kern1.3pt{=}\kern1.3pt\int_Y\tau \bar\psi e^{-u\tau}e^{s\bar\psi}\, d\mu_{\overline{\phi}} \kern1.3pt{+}\kern1.3pt O\bigg((u+s)\int_Y\tau\bar\psi e^{-u\tau}e^{s\bar\psi}\, d\mu_{\overline{\phi}}\bigg) \kern1.3pt{+}\kern1.3pt O(u^{\beta-\gamma-1} (u\kern1.3pt{+}\kern1.3pt s)). \end{align*} $$

Taking $s=0$ in this equation, we get that there exists $C>0$ so that

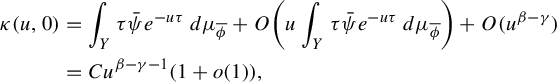$$ \begin{align*} \kappa(u,0)&=\int_Y\tau \bar\psi e^{-u\tau}\, d\mu_{\overline{\phi}} +O\bigg(u\int_Y\tau\bar\psi e^{-u\tau}\, d\mu_{\overline{\phi}}\bigg) +O(u^{\beta-\gamma} )\\ &=C u^{\beta-\gamma-1}(1+o(1)), \end{align*} $$

where in the last equality, we have used equation (4.1).

We estimate $\kappa _1,\ldots ,\kappa _7$ in equation (4.9). Note that differentiating once more in equation (4.6) and using the estimates in §4.1, $\int _Y\tau \bar \psi ^2 e^{-u\tau }\, d\mu _{\overline {\phi }}=Cu^{\beta -2\gamma -1}(1+o(1))$ . Thus, as $u,s\to 0$ ,

$$ \begin{align*} \kappa_1(u,s)=\int_Y\tau \bar\psi^2 e^{-u\tau}\, d\mu_{\overline{\phi}} +\int_Y\tau \bar\psi^2 (e^{s\bar\psi}-1)e^{-u\tau}\, d\mu_{\overline{\phi}} =Cu^{\beta-2\gamma-1}(1+o(1)). \end{align*} $$

By arguments already used in estimating quantities in proof of items (i) and (ii) above, $\kappa _2(u,s), \kappa _3(u,s),\kappa _4(u,s),\kappa _6(u,s)=o(u^{\beta -2\gamma -1})$ , as $u,s\to 0$ . Finally, by Lemma 4.1(i) (statement on $K_2$ ), $\|({\partial ^2}/{\partial s^2})({\partial }/{\partial u})v(u,s)\|_{\mathcal {B}_\theta }\ll u^{\beta -2\gamma -1}$ . Thus, $\kappa _5(u,s),\kappa _7(u,s)=o(u^{\beta -2\gamma -1})$ , as $u,s\to 0$ .

5 Proof of Proposition 2.6

Using the technical results in §4, we can proceed to the proof of Proposition 2.6. We recall that this is a refined version of Proposition 2.4 under somewhat stronger assumptions (that is, regular variation of the tail behaviour). In this sense, the task of this section is to go over the steps of the proof of Proposition 2.4 and obtain higher order expansions. From this proof, we recall that a first step is to refine the estimate on $({\partial }/{\partial s})({\partial }/{\partial u})\bar p(u,s)$ (see equation (3.10)). For the proof of Proposition 2.6, we shall need to understand $({\partial ^2}/{\partial s^2})({\partial }/{\partial u})\bar p(u,s)$ as $u,s\to 0$ .

Lemma 5.1. Assume the setup of Proposition 2.6 with a larger range of $\gamma $ , namely ${\gamma \in (\beta -1,\beta )}$ . There exist $C_2, C_3, C_4, C_5>0$ (varying from line to line) so that the following hold as $u,s\to 0$ .

1. (i) If $\beta /\gamma\ \in\ (1,2)$ , then $ ({\partial ^2}/{\partial s^2})({\partial }/{\partial u})\bar p(u,s)\ =\ -C_2s^{\beta /\gamma -2}(1\ +\ o(1)+ C_3 u^{\beta -2\gamma -1}(1+o(1)).$ Also, $({\partial }/{\partial s})({\partial }/{\partial u})\bar p(u,s)= C_4u^{\beta -\gamma -1}(1+o(1))+C_5 s u^{\beta -2\gamma -1}(1+o(1))$ .

2. (ii) If $\beta /\gamma =2$ , then $ ({\partial ^2}/{\partial s^2})({\partial }/{\partial u})\bar p(u,s)=-C_2\log (1/s)(1+o(1))+C_3 u^{-1}(1+o(1)).$ Also, $({\partial }/{\partial s})({\partial }/{\partial u})\bar p(u,s)= C_4u^{\beta -\gamma -1}(1+o(1))+ C_3s u^{-1}(1+o(1))-C_2 s\log (1/s)(1+o(1))$ .

3. (ii) If $\beta /\gamma \in (2,3)$ , then $ ({\partial ^3}/{\partial s^3})({\partial }/{\partial u})\bar p(u,s)\ =\ -C_2s^{\beta /\gamma -3}(1+o(1))\ {-} C_3 u^{\beta -3\gamma -1} (1+o(1)).$ Also, $({\partial ^2}/{\partial s^2})({\partial }/{\partial u})\bar p(u,s)|_{s=0}=- C_4u^{\beta -2\gamma -1} (1+o(1))+ C_3 s u^{\beta -3\gamma -1} (1+o(1))$ .

Proof. First, we recall from equation (3.10) that

$$ \begin{align*} \frac{\partial}{\partial s}\frac{\partial}{\partial u}\bar p(u,s) &= -\frac{({\partial}/{\partial u})\unicode{x3bb}(u,s)({\partial}/{\partial s})\unicode{x3bb}(u,s)}{\unicode{x3bb}(u,s)^2}+\frac{({\partial}/{\partial s})({\partial}/{\partial u})\unicode{x3bb}(u,s)}{\unicode{x3bb}(u,s)}. \end{align*} $$

Set $A(u,s):=({\partial }/{\partial u})\unicode{x3bb} (u,s)({\partial }/{\partial s})\unicode{x3bb} (u,s)$ and recall (for instance, from Lemma 4.2(iii)) that $\kappa (u,s)=({\partial }/{\partial s})({\partial }/{\partial u})\unicode{x3bb} (u,s)$ . Compute that

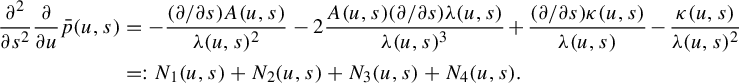$$ \begin{align*} \frac{\partial^2}{\partial s^2}\frac{\partial}{\partial u}\bar p(u,s) &= -\frac{({\partial}/{\partial s})A(u,s)}{\unicode{x3bb}(u,s)^2}-2\frac{A(u,s)({\partial}/{\partial s})\unicode{x3bb}(u,s) }{\unicode{x3bb}(u,s)^3} \kern1.3pt{+}\kern1.3pt\frac{({\partial}/{\partial s})\kappa(u,s)}{\unicode{x3bb}(u,s)}\kern1.3pt{-}\kern1.3pt\frac{\kappa(u,s)}{\unicode{x3bb}(u,s)^2}\\ &=:N_1(u,s)+N_2(u,s)+N_3(u,s)+N_4(u,s). \end{align*} $$

We provide the proof of item (i). Item (ii) follows by the same argument using the statements for the case $\beta /\gamma =2$ in Lemma 4.2(i) and (ii). Item (iii) follows by a similar argument after differentiating once more and using the statements for the case $\beta /\gamma \in (2,3)$ in Lemma 4.2(i) and (ii).

From the estimates of Lemma 4.2(i) and (ii) (the statements for the case $\beta /\gamma \in (1,2)$ ), it is easy to see that $N_2$ and $N_4$ do not contribute to the main asymptotics (because they go to a constant as $u,s\to 0$ ). We need to look at $N_1$ and $N_3$ .

The term $N_1(u,s)$ . Using the same notation as in Lemma 4.2(i) and (ii),

$$ \begin{align*} A(u,s)= (-\tau^*+d(u,s))(\bar\psi^*+ C s^{\beta/\gamma-1}+h(s)+h_0(s) +e(u,s) ) \end{align*} $$

and

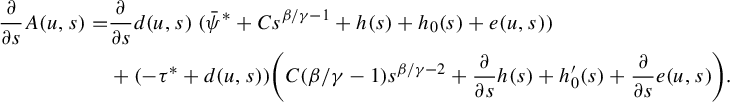$$ \begin{align*} \frac{\partial}{\partial s} A(u,s)=& \frac{\partial}{\partial s} d(u,s)\, (\bar\psi^*+ C s^{\beta/\gamma-1}+h(s)+h_0(s) +e(u,s) )\\ &+ (-\tau^*+d(u,s))\bigg( C(\beta/\gamma-1) s^{\beta/\gamma-2}+\frac{\partial}{\partial s} h(s)+h_0'(s) +\frac{\partial}{\partial s} e(u,s) \bigg).\end{align*} $$

Using all the estimates on $d, h_0, e$ in Lemma 4.2(i) and (ii) (the statements for the case $\beta /\gamma \in (1,2)$ ), we obtain that there exist $C_2, C_2'>0$ so that

$$ \begin{align*} \frac{\partial}{\partial s} A(u,s)&=-C_2 s^{\beta/\gamma-2}(1+o(1)) + C_2' u^{\beta-\gamma-1}(1+o(1)), \end{align*} $$

which gives the asymptotics for $N_1(u,s)$ . In the previous displayed equation, apart from the estimates on $({\partial }/{\partial s}) d(u,s)$ and $({\partial }/{\partial s}) e(u,s)$ , we have used the immediate consequence of Lemma 4.2(ii) that $d(u,s)=O(s u^{\beta -\gamma -1})$ and that $ e(u,s)= o(s u^{\beta -\gamma -1})$ .

The term $N_3(u,s)$ . By Lemma 4.2(iii) (the statement for the case $\beta /\gamma \in (1,2)$ ), $({\partial }/{\partial s})\kappa (u,s)=C_3 u^{\beta -2\gamma -1}(1+o(1))$ for some $C_3>0$ . This gives the same asymptotics for $N_3$ . Therefore,

$$ \begin{align*} N_1(u,s)+N_3(u,s)=-C_2 s^{\beta/\gamma-2}(1+o(1))+C_3 u^{\beta-2\gamma-1}(1+o(1)),\end{align*} $$

which gives the first statement in item (i).

The second statement in item (i) follows immediately from the first together with the asymptotics of $\kappa (u,0)$ in Lemma 4.2(iii).

We can now proceed to the following proof.

Proof of Proposition 2.6

We redo all steps in the proof of Proposition 2.4(ii) using Lemma 4.2.

Recall $\bar p(u,s)=\log \unicode{x3bb} (u,s)$ . The analogue of equation (3.8) is

(5.1) $$ \begin{align} \frac{\partial}{\partial u}\bar p(u,s)=-\tau^*+D(u,s),\quad \frac{\partial}{\partial s}\bar p(u,s)= \bar\psi^*+E(u,s), \end{align} $$

where:

1. (a) $D(u,s)$ satisfies the same properties as $d(u,s)$ in Lemma 4.2(i);

2. (b) $E(u,s)$ satisfies the same properties as $e(u,s)$ in Lemma 4.2(ii).

By Lemma 4.2(i) and (ii), we have the following refined version of equation (3.9) (with C varying from line to line):

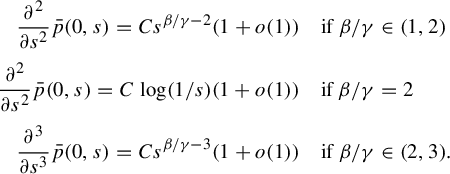(5.2) $$ \begin{align} \nonumber \frac{\partial^2}{\partial s^2}\bar p(0,s)=Cs^{\beta/\gamma-2}(1+o(1)) \quad&\text{if }\beta/\gamma\in (1,2)\\[1mm] \nonumber \frac{\partial^2}{\partial s^2}\bar p(0,s)=C\log(1/s)(1+o(1)) \quad & \text{if }\beta/\gamma=2 \\[1mm] \frac{\partial^3}{\partial s^3}\bar p(0,s)=Cs^{\beta/\gamma-3}(1+o(1)) \quad &\text{if }\beta/\gamma\in (2,3). \end{align} $$

The analogue of equation (3.12) for any small $u_0>0$ is

$$ \begin{align*} \bar p(u_0,s)-\bar p(0,s)=-\tau^* u_0+ \int_0^{u_0} D(u,s)\, du:=-\tau^* u_0+ L(u_0,s), \end{align*} $$

where $D(u,s)$ satisfies the same properties as $d(u,s)$ in Lemma 4.2(i). Moreover, as in the proof of Proposition 2.4(ii),

(5.3) $$ \begin{align} \frac{\partial}{\partial s}D(u,s)=\frac{\partial}{\partial s}\frac{\partial}{\partial u}\bar p(u,s). \end{align} $$

By the argument used in the proof of Proposition 2.4 in deriving equation (3.15),

(5.4) $$ \begin{align} u_0'(s) = \frac{({\partial}/{\partial s}) M(u_0,s)}{\tau^*-({\partial}/{\partial u_0}) M(u_0,s)}, \end{align} $$

where, as in the proof of Proposition 2.4,

(5.5) $$ \begin{align} M(u_0,s)=L(u_0,s)+\bar p(0,s) \quad \text{with } \frac{\partial}{\partial u_0} L(u_0,s)=D(u_0,s). \end{align} $$

Differentiating equation (5.4) once more in s,

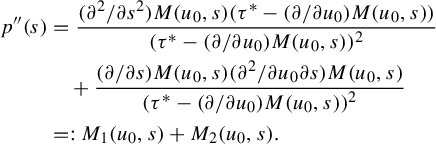(5.6) $$ \begin{align} \nonumber p"(s)& =\frac{({\partial^2}/{\partial s^2}) M(u_0,s)(\tau^*-({\partial}/{\partial u_0}) M(u_0,s)) } {(\tau^*-({\partial}/{\partial u_0}) M(u_0,s))^2}\\ \nonumber&\quad +\frac{({\partial}/{\partial s}) M(u_0,s)({\partial^2}/{\partial u_0\partial s}) M(u_0,s)}{(\tau^*-({\partial}/{\partial u_0}) M(u_0,s))^2}\\ &=:M_1(u_0,s)+M_2(u_0,s). \end{align} $$

We complete the proof of item (i), that is, we treat the case $\beta /\gamma \in (1,2)$ using the estimates in Lemma 4.2. The precise asymptotics in item (ii) for the case $\beta /\gamma = 2$ follow by the same argument using the corresponding estimates in Lemma 4.2. Item (iii), the case $\beta /\gamma \in (2,3)$ , (after taking one more derivative in s) is similar and omitted.

Proof of (i), the case $\mathit {\beta /\gamma \in (1,2)}$ .

The term $\mathit {M_1(u_0,s)}$ defined in equation (5.6). Differentiating equation (5.5),

(5.7) $$ \begin{align} \frac{\partial}{\partial s} M(u_0,s)=\frac{\partial}{\partial s} L(u_0,s)+\frac{\partial}{\partial s}\bar p(0,s). \end{align} $$

Using equations (3.11), (5.3) and Lemma 5.1(i),

$$ \begin{align*} \frac{\partial}{\partial s} L(u_0,s)&=\int_0^{u_0}\frac{\partial}{\partial s}D(u,s)\, du = C_4 u_0^{\beta-\gamma}(1+o(1))+ C_3 s\, u_0^{\beta-2\gamma}(1+o(1)). \end{align*} $$

By Proposition 2.4(ii), $p(s)=u_0(s)={\bar p(0,s)}/{\tau ^*}=s ({\bar \psi ^*}/{\tau ^*})(1+o(1))$ , as $s\to 0$ . Thus,

$$ \begin{align*} \frac{\partial}{\partial s} L(u_0,s)&=C_4 s^{\beta-\gamma}(1+o(1))+ C_3 s^{\beta-2\gamma+1}(1+o(1))=C_4 s^{\beta-\gamma}(1+o(1)), \end{align*} $$

where in the last equality, we have used that $\gamma <1$ .

By Lemma 4.2(ii), $({\partial }/{\partial s})\bar p(0,s)=\bar \psi ^*+Cs^{\beta /\gamma -1}(1+o(1))$ . Since $\beta>\gamma $ ,

(5.8) $$ \begin{align} \frac{\partial}{\partial s} M(u_0,s) =\bar\psi^*+Cs^{\beta/\gamma-1}(1+o(1))=\bar\psi^*(1+o(1)). \end{align} $$

Differentiating equation (5.7) once more in s and using equation (5.2),

$$ \begin{align*} \frac{\partial^2}{\partial s^2} M(u_0,s)=\frac{\partial^2}{\partial s^2} L(u_0,s)+\frac{\partial^2}{\partial s^2}\bar p(0,s) =\frac{\partial^2}{\partial s^2} L(u_0,s)+Cs^{\beta/\gamma-2}(1+o(1)). \end{align*} $$

Next, recall equation (5.3) and note that $({\partial ^2}/{\partial s^2})D(u,s)=({\partial ^2}/{\partial s^2})({\partial }/{\partial u})\bar p(u,s)$ . By Lemma 5.1(i), $ ({\partial ^2}/{\partial s^2})({\partial }/{\partial u})\bar p(u,s)=-C_2s^{\beta /\gamma -2}(1+o(1)+C_3 u^{\beta -2\gamma -1}(1+o(1)).$ Also, recall that $u_0(s)=s ({\bar \psi ^*}/{\tau ^*})(1+o(1))$ , as $s\to 0$ for $C_2, C_3>0$ . Thus,

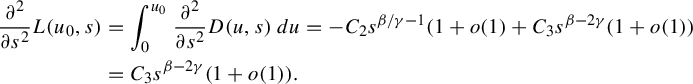(5.9) $$ \begin{align} \frac{\partial^2}{\partial s^2} L(u_0,s)&=\int_0^{u_0}\frac{\partial^2}{\partial s^2}D(u,s)\, du =-C_2s^{\beta/\gamma-1}(1+o(1)+C_3 s^{\beta-2\gamma}(1+o(1))\nonumber\\ &=C_3 s^{\beta-2\gamma}(1+o(1)). \end{align} $$

Remark 5.2. If we do not assume regular variation for the tail $\mu _{\overline \phi }(\psi _0\ge x)=\mu _{\overline \phi }(\tau ^\gamma \ge x)$ , we can still use the same steps as above in obtaining equation (5.9) and rougher calculations, similar to those used in obtaining equation (3.5), to show that $|({\partial ^2}/{\partial s^2}) L(u_0,s)|=O(s^{\gamma (\beta /\gamma -2)})$ . In particular, following these steps, one has that if $\psi _0\in L^{q_1}(\mu _{\overline \phi })$ , then $|({\partial ^2}/{\partial s^2}) L(u_0,s)|=O(s^{a(q_1-2)})$ for some $a>0$ , so $|({\partial ^2}/{\partial s^2}) L(u_0,s)|=o(1)$ as ${s\to 0}$ .

Putting the previous three displayed equations together and noticing that $s^{\beta -2\gamma }>s^{\beta /\gamma -2}$ (since $\gamma <1$ ), we obtain

(5.10) $$ \begin{align} \frac{\partial^2}{\partial s^2} M(u_0,s)=C_3 s^{\beta-2\gamma}(1+o(1)). \end{align} $$

We have ${1}/({\tau ^*-({\partial }/{\partial u_0}) M(u_0,s)})={1}/({\tau ^*-D(u_0,s)}) ={1}/{\tau ^*}(1+O(D(u_0,s))$ as in the proof of Proposition 2.4(ii). Using the properties of $D_0(u,s)$ in item (a) after equation (3.8) (both smoothness in s and asymptotics of $D(u_0, 0)$ ), and using that $u_0(s)=O(s)$ , we have

$$ \begin{align*} \frac{1}{\tau^*-({\partial}/{\partial u_0}) M(u_0,s)}=\frac{1}{\tau^*}(1+O(s^{\beta-1}+s)) \end{align*} $$

as $s\to 0$ . This, together with equation (5.10), gives that as $s\to 0$ ,

(5.11) $$ \begin{align} M_1(u_0,s)=C_3 s^{\beta-2\gamma}(1+o(1)). \end{align} $$

The term $\mathit {M_2(u_0,s)}$ defined in equation (5.6).

Differentiating equation (5.7) once more in $u_0$ , $({\partial ^2}/{\partial u_0\partial s}) M(u_0,s)=({\partial ^2}/{\partial u_0\partial s}) L(u_0,s)$ . Recall that $ ({\partial }/{\partial s}) L(u_0,s)=\int _0^{u_0}({\partial }/{\partial s})D(u,s)\, du$ and that $D(u,s)$ is uniformly continuous in u. Thus, $({\partial ^2}/{\partial u_0\partial s}) M(u_0,s)= ({\partial }/{\partial s})D(u_0,s)$ . Recalling equation (5.3),

$$ \begin{align*} \frac{\partial^2}{\partial u_0\partial s} M(u_0,s)=\frac{\partial}{\partial s}\frac{\partial}{\partial u}\bar p(u,s)\bigg|_{u=u_0}. \end{align*} $$

By Lemma 5.1(i),

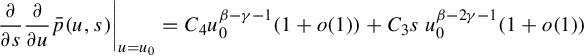$$ \begin{align*} \frac{\partial}{\partial s}\frac{\partial}{\partial u}\bar p(u,s)\bigg|_{u=u_0} = C_4 u_0^{\beta-\gamma-1}(1+o(1))+ C_3 s\, u_0^{\beta-2\gamma-1}(1+o(1)) \end{align*} $$

for $C_3, C_4>0$ . Since $u_0(s)=s ({\bar \psi ^*}/{\tau ^*})(1+o(1))$ , as $s\to 0$ ,

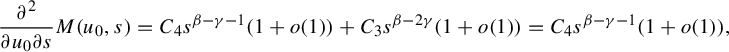$$ \begin{align*} \frac{\partial^2}{\partial u_0\partial s} M(u_0,s)=C_4 s^{\beta-\gamma-1}(1+o(1))+ C_3 s^{\beta-2\gamma}(1+o(1))=C_4 s^{\beta-\gamma-1}(1+o(1)), \end{align*} $$

where in the last equation, we have used again that $\gamma <1$ .

Recalling equation (5.8) and that ${1}/({\tau ^*-({\partial }/{\partial u_0}) M(u_0,s)})= ={1}/{\tau ^*}(1+o(1))$ , we have $M_2(u_0,s)= ({\bar \psi ^*}/{\tau ^*})C_4 s^{\beta -\gamma -1}(1+o(1))$ . This together with equation (5.11) gives the conclusion after recalling again that $\gamma <1$ , which ensures that $s^{\beta -\gamma -1}> s^{\beta -2\gamma }$ .

6 Proofs of the main abstract results

The proofs of the main results will make use of the restricted pressure. Analogous to [RS, Definition 5.1], we define

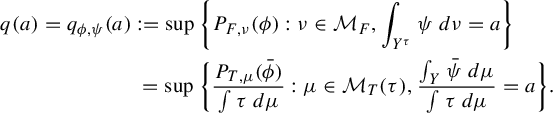$$ \begin{align*} q(a) = q_{\phi, \psi}(a) & := \sup\bigg\{P_{F, \nu}(\phi):\nu\in\mathcal{M}_{F},\int_{Y^\tau}\psi\, d\nu=a \bigg\} \\ &\ = \sup\bigg\{\frac{P_{T, \mu}(\bar\phi)}{\int\tau~d\mu}:\mu\in\mathcal{M}_T(\tau),\frac{\int_{Y}\bar\psi\, d\mu}{\int\tau~d\mu}=a \bigg\}. \end{align*} $$

6.1 Proof of Theorem 2.8

Proof of Theorem 2.8

Given Proposition 2.4 with $q_1>3$ , the details are very similar to those in [RS, Proof of Lemma 5.2] (and also the main line of the argument in [RS, Proof of Proposition 6.1]). We recall most of the details, partly for completeness, partly because our setup is different (unbounded potential but more restricted $\psi $ ).

By Proposition 2.4(ii), $p'(0)={\int _Y\overline {\psi }\, d\mu _{\bar \phi }}/{\int _Y\tau \, d\mu _{\bar \phi }}=\int _{Y^\tau }\psi \, d\nu _{\phi }=a_0$ . By assumption, $\nu _{\phi }$ is the unique equilibrium measure for $\phi $ . Since $p"(s) \geq 0$ is continuous with $p"(0) = \sigma ^2> 0$ (by Proposition 2.4), $p'$ is strictly increasing near $0$ .

Given $h\in (0, \delta _0)$ , for $\delta _0$ as in Proposition 2.4, let $a\in (p'(0), p'(h))$ . By the intermediate value theorem, there exists $s\in (0,h)$ so that $p'(s)=a$ . By Proposition 2.4(ii) and (iii), the second derivative is well defined whenever $q_1>2$ .

We next show that p is strictly convex in our domain of interest. Throughout the rest of the proof, let $K> \sigma ^2$ , so $\delta _0({\sigma ^2}/{K})<\delta _0$ . By the assumption $q_1> 3$ , the third derivative $p"'$ is well defined and we can assume $|p"'|<K$ by taking K larger if necessary. We use this to show strict convexity and that the solution to the equation $p'(s)=a$ in s is unique. To see this, we recall the argument by contradiction in [RS, Proof of Lemma 5.2]. As in [RS, Proof of Lemma 5.2], if there exists $s_0\ne s, s\in (0,\delta _0({\sigma ^2}/{K}))$ so that $p'(s_0)=a$ , then $p"$ would have vanished in this interval. This is not possible because for some $s'\in (0,s)$ ,

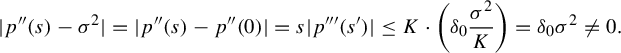$$ \begin{align*} |p"(s)-\sigma^2|=|p"(s)-p"(0)|= s |p"'(s')|\le K \cdot \bigg(\delta_0\frac{\sigma^2}{K}\bigg)=\delta_0\sigma^2\ne 0. \end{align*} $$

Next, we find useful relationships between a, s and $\nu _s$ for the appropriate s. For the unique s so that $p'(s)=a$ , we know that $R(u,s)$ satisfies the spectral gap: this follows since $R(0,0)$ has a spectral gap in $\mathcal {B}$ and $R(u,s)$ is continuous in $u, s$ (by Lemma 3.1). Thus, the potential $\overline {\phi +s\psi -p(s)}$ has a unique equilibrium state ${\mu }_s$ . This projects to an equilibrium state $\nu _s$ for the potential $\phi +s\psi $ (the unique such measure), as follows. First, note that from the Gibbs property and since $s, p(s)>0$ and $\bar \psi <\infty $ , we get

$$ \begin{align*} \int\tau~d\mu_s\ll \int \tau e^{s\bar\psi-\tau p(s) }~d\mu_{\bar\phi} \ll \int\tau~d\mu_{\bar\phi}<\infty, \end{align*} $$

so $\mu _s\in \mathcal {M}_T(\tau )$ and we obtain $\nu _s\in \mathcal {M}_F$ from equation (2.2). Moreover, by the Abramov formula, $P_{F, \nu _s}(\phi +s\phi -p(s)) =0$ , which first implies that $\nu _s$ is an equilibrium state for $\phi +s\psi $ . It is also standard to show that this is the unique equilibrium state for this potential and that $\int \psi ~d\nu _s = p'(s) =a$ , as above. Moreover, if $\nu \in \mathcal {M}_F$ has $P_\nu (\phi )>P_{\nu _s}(\phi )$ and $\int \psi ~d\nu =a$ , then

$$ \begin{align*}P_\nu(\phi+s\psi) = P_\nu(\phi)+sa>P_{\nu_s}(\phi)+sa = P_{\nu_s}(\phi+s\psi)=p(s),\end{align*} $$

which is a contradiction. Therefore,

(6.1) $$ \begin{align} P_\nu(\phi)\le p(s) - s\int\psi~d\nu_s= P_{\nu_s}(\phi)=q(a) \end{align} $$

for any $\nu \in \mathcal {M}_F$ with $\int \psi ~d\nu =a$ .

The final task here is to get a relation for $a-a_0$ in terms of $P(\phi )-P_{\nu }(\phi )$ . Recall $q_1> 3$ . By Proposition 2.4(ii), $p"'$ is $C^{q_1-[q_1]}$ . Thus,

$$ \begin{align*} p(s) = p(0)+ sp'(0)+ \frac{s^2}{2}p"(0)+ \frac{s^3}{6}p"'(0)+ O(s^{3+{\epsilon}}) \end{align*} $$

for some ${\epsilon }>0$ , so $p'(s) = p'(0)+ sp"(0)+({s^2}/{2})p"'(0)+O(s^{2+{\epsilon }})$ . Then, for s so that $p'(s)=a$ and recalling that $p"(0)=\sigma ^2$ ,

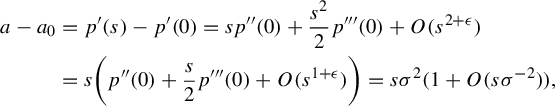$$ \begin{align*} a-a_0&=p'(s)-p'(0)=sp"(0)+\frac{s^2}{2}p"'(0)+O(s^{2+{\epsilon}})\\ &= s\bigg(p"(0)+\dfrac{s}{2}p"'(0)+O(s^{1+{\epsilon}})\bigg) =s\sigma^2(1+O(s\sigma^{-2})), \end{align*} $$

where in the last step, we have used that $s\in (0,\delta _0({\sigma ^2}/{K}))$ and that $|p"'(0)|<K$ . Hence,

(6.2) $$ \begin{align} s=\frac{a-a_0}{\sigma^2}(1+O(s^{1+{\epsilon}}\sigma^{-2})). \end{align} $$

Next, arguing word for word as in the [RS, Proof of Lemma 5.2, item (4)], $q(a_0)=P_{\nu _\phi }(\phi )$ and since, by assumption, $P_{\nu _\phi }(\phi )=p(0)=0$ , we have $q(a_0)=0$ . This, together with equation (6.1), the fact that $a=p'(s)$ , the expansions of $p(s)$ and $p'(s)$ , and equation (6.1), implies that for some ${\epsilon }>0$ ,

$$ \begin{align*} q(a_0)-q(a)&=sp'(s)-p(s) = \frac{s^2}{2}\sigma^2+ \frac{s^3}{6}p"'(0)+O(s^{3+{\epsilon}}). \end{align*} $$

This, together with equation (6.2), gives

$$ \begin{align*} q(a_0)-q(a)=\frac{(a-a_0)^2}{2\sigma^2}(1+O(\sigma^{-2}(a-a_0))). \end{align*} $$

So for $\nu \in \mathcal {M}_F$ with $\int \psi ~d\nu =a$ , the above equation and equation (6.1) imply

(6.3) $$ \begin{align} P_{\nu_\phi}(\phi)- P_\nu(\phi) \ge P_{\nu_\phi}(\phi)- P_{\nu_s}(\phi) = \frac{(a-a_0)^2}{2\sigma^2} (1+O(\sigma^{-2}(a-a_0))). \end{align} $$

Making $a-a_0 = \int \psi ~d\nu - \int \psi ~d\nu _\phi $ subject of this equation gives

$$ \begin{align*} \int\psi~d\nu- \int\psi~d\nu_\phi \le C_{\phi, \psi}\sqrt2 \sigma\sqrt{P_{\nu_\phi}(\phi)- P_\nu(\phi)}, \end{align*} $$

where the constant $C_{\phi , \psi } \geq 1$ tends to $1$ as $\int \psi \, d\nu \to \int \psi \, d\nu _{\phi }$ . Continuing with $\nu _s$ , the equilibrium state of $\phi + s\psi $ , we get the more precise form

$$ \begin{align*} \int\psi~d\nu_s - \int\psi~d\nu_\phi = \sqrt2 \sigma\sqrt{ P_{\nu_\phi}(\phi)- P_{\nu_s}(\phi) } + O(P_{\nu_\phi}(\phi)- P_{\nu_s}(\phi)), \end{align*} $$

which can be rewritten as equation (2.7) as required.

6.2 Proof of Theorem 2.9

We shall need the following fact, which relies on the positivity of $p"(s)$ given by Proposition 2.6.

Lemma 6.1. Take $\beta /\gamma \in (1,3)$ and $a \in (p'(0), p'(\delta _0))$ , where $\delta _0$ is as in Proposition 2.4. Then, $p"(s)>0$ for $s\in (0,\delta _0)$ and there exists a unique $s\in (0,\delta _0)$ satisfying $p'(s) = a$ .

Proof. By Proposition 2.6, both for $\beta /\gamma \in (1,2]$ and for $\beta /\gamma \in (2,3)$ , the first derivative $p'$ is bounded. For $\beta /\gamma \in (1,2)$ , the positivity of $p"(s)$ is given by Proposition 2.6(i). For the case $\beta /\gamma \in (2,3)$ , Proposition 2.4(iii) ensures that $p"(0)=\sigma ^2$ . This together with Proposition 2.6(ii) gives the positivity of $p"(s)$ when $\beta /\gamma \in (2,3)$ . It follows that $p'$ is a strictly increasing function and the conclusion follows.

Proof of Theorem 2.9

Let $a_0=\int \psi ~d\nu _\phi $ and $a=\int \psi ~d\nu $ , and assume $a>a_0$ . By Lemma 6.1, $p'(s)=a$ has a unique solution. This allows us to repeat the argument recalled in obtaining equation (6.1) and to obtain $q(a)=p(s)-sa$ . As in the proof of Theorem 2.8, recall that $q(a_0)=P_{\nu _\phi }(\phi )$ and $q(a)=P_{\nu _s}(\phi )$ , where $\nu _s$ is the unique equilibrium measure for $\psi +s\psi $ . Let $\nu $ be any F-invariant probability measure so that $a=\int _{Y^\tau }\psi \, d\nu>a_0=\int _{Y^\tau }\psi \, d\nu _{\phi }$ .

Proof of item (a), the case $\mathit {\beta /\gamma \in (1,2]}$ . Note that $a-a_0=p'(s)-p'(0)$ . Using Proposition 2.6(i),

$$ \begin{align*} a-a_0= s p"(s) (1+o(1))=C_2\, s\, s^{\beta-\gamma-1}(1+o(1))=C_2s^{\beta-\gamma}(1+o(1)) \end{align*} $$

and so,

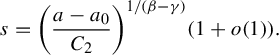(6.4) $$ \begin{align} s=\bigg(\frac{a-a_0}{C_2}\bigg)^{1/(\beta-\gamma)}(1+o(1)). \end{align} $$

Since $q(a_0)=0$ , $q(a_0)-q(a) = sp'(s)-p(s)$ . The Taylor expansion with remainder gives $p(y)=p(x)+p'(x)(y-x)+\int _x^y (y-\xi ) p"(\xi )\, d\xi $ . Taking $y=0$ and $x=s$ , $ q(a_0)-q(a) =sp'(s)-p(s)=\int _0^s \xi p"(\xi )\, d\xi. $ By Proposition 2.6(i), we have

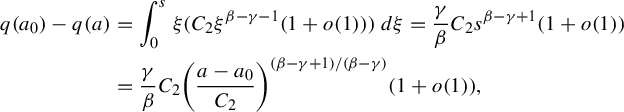(6.5) $$ \begin{align} q(a_0)-q(a) &=\int_0^s \xi (C_2 \xi^{\beta-\gamma-1}(1+o(1)))\, d\xi= \frac{\gamma}{\beta} C_2 s^{\beta-\gamma+1} (1+o(1)) \nonumber \\ &=\frac{\gamma}{\beta} C_2\bigg(\frac{a-a_0}{C_2}\bigg)^{({\beta-\gamma+1})/({\beta-\gamma})}(1+o(1)), \end{align} $$

where in the second equality, we have used equation (6.4). So, there is $c_2> 0$ such that

$$ \begin{align*} a-a_0=c_2 (q(a_0)-q(a))^{({\beta-\gamma})/({\beta-\gamma+1})}(1+o(1)). \end{align*} $$

For an arbitrary measure $\nu $ , we have $P_{\nu _\phi }(\phi )- P_\nu (\phi ) \ge P_{\nu _\phi }(\phi )- P_{\nu _s}(\phi )$ as in equation (6.3), and we have

$$ \begin{align*} \int\psi\,d\nu-\int\psi\,d\nu_{\phi}\le c_2 (P_{\nu_\phi}(\phi)-P_\nu(\phi))^{({\beta-\gamma})/({\beta-\gamma+1})} \end{align*} $$

as required. For the equilibrium state $\nu _s$ itself, we have the more precise estimate with $c_2 = ({\beta }/{\gamma })C_2$ :

$$ \begin{align*} \int\psi\,d\nu_s-\int\psi\,d\nu_{\phi} = c_2 (P_{\nu_\phi}(\phi)-P_{\nu_s}(\phi))^{({\beta-\gamma})/({\beta-\gamma+1})} (1+o(1)), \end{align*} $$

which can be rewritten to equation (2.8).

Proof of item (b), the case $\mathit {\beta /\gamma \in (2,3)}$ . Using Proposition 2.6(ii) and Taylor’s theorem, we have

(6.6) $$ \begin{align} a-a_0&= p'(s) - p'(0) = s p^{\prime\prime}(0) + \int_0^s \xi p^{\prime\prime\prime}(\xi) \, d\xi = s\sigma^2 + O(s^{\beta-2\gamma+1}). \end{align} $$

Therefore,

(6.7) $$ \begin{align} s=\frac{a-a_0}{\sigma^2}(1+O(s^{\beta-2\gamma})). \end{align} $$

By Taylor’s theorem, $p(s)=p(0)+ sp^{\prime }(0)+ {s^2}/{2}p^{\prime \prime }(0)+\int _0^s\xi ^2 p^{\prime \prime \prime }(\xi )\, d\xi $ . This, together with Proposition 2.6(ii) (and recalling $p^{\prime \prime }(0)=\sigma ^2$ and $p(0)=0$ ), gives

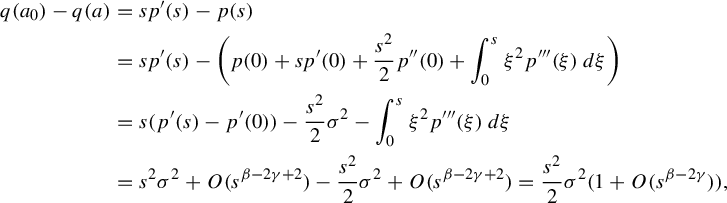$$ \begin{align*} q(a_0)-q(a) &=sp^{\prime}(s)-p(s)\\ &=sp^{\prime}(s) - \bigg(p(0) + sp^{\prime}(0) + \frac{s^2}{2} p^{\prime\prime}(0) + \int_0^s \xi^2 p^{\prime\prime\prime}(\xi) \, d\xi \bigg)\\ &=s(p^{\prime}(s)-p^{\prime}(0)) - \frac{s^2}{2} \sigma^2 - \int_0^s \xi^2 p^{\prime\prime\prime}(\xi) \, d\xi\\ &=s^2\sigma^2 + O(s^{\beta-2\gamma +2}) - \frac{s^2}{2} \sigma^2 + O(s^{\beta-2\gamma +2}) = \frac{s^2}{2} \sigma^2 (1 + O(s^{\beta-2\gamma})), \end{align*} $$

where we used equation (6.6) in the last line. This, together with equation (6.7), gives

(6.8) $$ \begin{align} q(a_0)-q(a) &= \frac{(a-a_0)^2}{2\sigma^2} ( 1+ O((a-a_0)^{\beta-2\gamma}) ). \end{align} $$

Since, for an arbitrary measure $\nu $ , we have again

$$ \begin{align*} \int\psi\,d\nu-\int\psi\,d\nu_{\phi}\le c_3 \sqrt{ P_{\nu_\phi}(\phi)-P_\nu(\phi)} \end{align*} $$

for some $c_3 \geq 1$ . For the equilibrium state $\nu _s$ itself, we have the more precise estimate:

$$ \begin{align*} \int\psi\,d\nu_s-\int\psi\,d\nu_{\phi} = \sigma \sqrt{2} \sqrt{ P_{\nu_\phi}(\phi)-P_{\nu_s}(\phi) } ( 1+O((P_{\nu_\phi}(\phi)-P_{\nu_s}(\phi) )^{({\beta-2\gamma})/{2}}) ). \end{align*} $$

This can be rewritten to equation (2.9)

6.3 When $a=\int \psi ~d\nu $ is much larger than $\int \psi ~d\nu _\phi $

Proof of Theorem 2.14

First notice that from assumption (GM1) and Abramov’s formula that $\int \psi ~d\nu <C_0$ , so $C_{\phi , \psi }^{\prime \prime }:=\max \{\int \psi ~d\nu _\phi , C_0\}$ and set $\psi ^{\prime }:={\psi }/{C_{\phi , \psi }^{\prime \prime }}$ . We will use $q= q_{\phi , \psi ^{\prime }}$ and (implicitly) $p=p_{\phi , \psi ^{\prime }}$ here.

We follow the proof of [RS, Theorem 7.1]. The following is an analogue of [RS, Lemma 5.1].

Lemma 6.2.

1. (a) $q= q_{\phi , \psi ^{\prime }}$ is well defined and finite on $(\int \psi ^{\prime } d\nu _\phi , \sup _{\nu \in \mathcal {M}_F} \int \psi ^{\prime } d\nu )$ ;

2. (b) $q= q_{\phi , \psi }$ is concave on the domain on $(\int \psi ~d\nu _\phi , \sup _{\nu \in \mathcal {M}_F} \int \psi ^{\prime }~d\nu )$ .

Proof. For part (a), we follow the proof of [RS, Lemma 5.1], but since in general we do not have information on $p_{\phi , \psi ^{\prime }}(t)$ for $t<0$ , or the topological entropy of F, we start by assuming that $a\in (\int \psi ^{\prime }~d\nu _\phi , \sup _{\nu \in \mathcal {M}_F} \int \psi ^{\prime }~d\nu )$ . Note that the theory above (more precisely, the arguments used inside the proofs of Theorems 2.8 and 2.9) shows that q is well defined in a subset of this set, but here we look to extend this. The choice of a implies there exist $\nu _1, \nu _2\in \mathcal {M}_F$ such that

$$ \begin{align*} \int\psi^{\prime}~d\nu_1<a<\int\psi^{\prime}~d\nu_2, \end{align*} $$

so as in [RS, Lemma 5.1], $\int \psi ^{\prime } d\nu =a$ for some convex combination of $\nu _1$ and $\nu _2$ , and the supremum defining q is over a non-empty set and it is well defined. The same argument pushed to the suspension flow of [RS, Lemma 5.1] implies that $q(a)>-\infty $ .

Finally, the proof of part (b) is identical to the latter part of the proof of [RS, Lemma 5.1].

For the next step, we follow a slightly coarser version of the proof of [RS, Corollary 5.1(2)]. The first step is to show that q is strictly decreasing. We note that the proofs of Propositions 2.4 or 2.6 imply that p is analytic in some interval $({\epsilon }_1, {\epsilon }_2)$ for ${\epsilon }_1, {\epsilon }_2>0$ , where ${\epsilon }_1$ can be taken arbitrarily close to 0. The same arguments as in [RS, Lemma 5.2], see in particular equation (5.3), then also imply that q is differentiable and strictly concave on some interval $(a_0^{\prime }, a_1)$ , where $a_0^{\prime }$ can be taken arbitrarily close to $a_0=\int \psi ^{\prime }~d\nu _\phi =p^{\prime }(0)$ , and moreover $q^{\prime }(p^{\prime }(t))=-t$ for $p^{\prime }(t)\in (a_0^{\prime }, a_1)$ . The key fact we then take from this is that $q(a_1)<q(a_0)$ , so we set $\eta := ({q(a_0)-q(a_1)})/({a_1-a_0})>0$ . Then, since Lemma 6.2 implies that q is concave for $a>a_0$ , so for $a>a_1$ , we have $q(a)-q(a_0)< -\eta (a-a_0)$ .

Given that $a=\int \psi ^{\prime }~d\nu $ , as in the proof of Theorem 2.8 or 2.9, the definition of q implies $P_\nu (\phi )\le q(a)$ and hence we can interpret the inequality above as: if $a\ge a_1$ , then

(6.9) $$ \begin{align} q(a_0)-q(a)\ge \eta(a-a_0)\Longrightarrow \int\psi^{\prime}~d\nu-\int\psi^{\prime}~d\nu_\phi\le \frac1{\eta} (P(\phi)-P_\nu(\phi)). \end{align} $$

Then, following the argument of the proof of [RS, Theorem 7.1], from equation (6.9), if $\int \psi ~d\nu>a_1$ , then

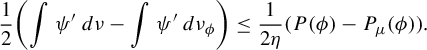$$ \begin{align*}\frac12\bigg(\kern-2pt\int\psi^{\prime}~d\nu-\int\psi^{\prime}~d\nu_\phi\bigg)\le \frac1{2\eta} (P(\phi)-P_\mu(\phi)).\end{align*} $$

Also then, noticing that $\frac 12(\int \psi ^{\prime }~d\nu -\int \psi ^{\prime }~d\nu _\phi )\le 1$ , we trivially have

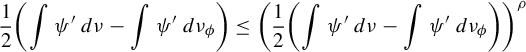$$ \begin{align*}\frac12\bigg(\kern-2pt\int\psi^{\prime}~d\nu-\int\psi^{\prime}~d\nu_\phi\bigg)\le \bigg(\frac12\bigg(\kern-2pt\int\psi^{\prime}~d\nu-\int\psi^{\prime}~d\nu_\phi\bigg)\bigg)^\rho\end{align*} $$

for any $\rho \in (0,1)$ (for example, $\rho =1/2$ ). Thus,

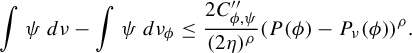$$ \begin{align*}\int\psi~d\nu-\int\psi~d\nu_\phi\le \frac{2C_{\phi, \psi}^{\prime\prime}}{(2\eta)^\rho}(P(\phi)-P_\nu(\phi))^\rho.\end{align*} $$

We set $C_{\phi , \psi }^{\prime }$ to be the maximum of $ ({2C_{\phi , \psi }^{\prime \prime }}/{(2\eta )^\rho })$ and the constant coming from our main theorems.

7 Applications

We provide examples of systems, both of discrete and continuous time, for which our main results apply. These are systems with weak forms of hyperbolicity that have not been studied before from this point of view.

7.1 Intermittent interval maps

Zweimüller [Z] introduced a class of interval maps $f:[0,1] \to [0,1]$ that he called AFN maps, that is, non-uniformly expanding maps with finitely many branches, finitely many neutral fixed points and satisfying Adler’s distortion property ( $f^{\prime \prime }/f^{\prime 2}$ bounded). Note that AFN maps are, in general, non-Markov. We stress that these are maps with weak hyperbolicity properties. Let $\alpha \in (0,1)$ and $b\in (0, 1]$ consider the family of AFN maps defined by

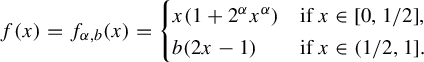$$ \begin{align*} f(x) = f_{\alpha, b}(x) = \begin{cases} x(1+ 2^\alpha x^\alpha) & \text{if } x\in [0, 1/2],\\ b(2x-1) & \text{if } x\in (1/2, 1]. \end{cases} \end{align*} $$

It follows from [Z] that for this range of values of the parameters $\alpha $ and b, there exists an absolutely continuous probability measure $\mu $ . Moreover, the first return time map to $Y= (1/2, 1]$ is uniformly expanding, although it may not be Markov. In [BT, §9], a Gibbs–Markov inducing scheme for Y with return time $\tau $ is constructed. That is, there exists a countable partition of Y so that $\tau $ is constant on each of the elements of the partition and the map $T:Y\to Y$ defined by $T=f^\tau $ is Gibbs–Markov. The map T can be thought of as a discrete suspension of f with roof function $\tau $ . Moreover, for a potential $\psi :[0,1] \to \mathbb {R}$ , its induced version $\bar \psi : Y \to \mathbb {R}$ is defined by $\bar \psi = \sum _{j=0}^{\tau -1} \psi \circ f^j$ . In particular, our main results can be applied to this discrete time system. We now verify that under certain conditions, the assumptions of our results are indeed satisfied. We begin with Theorem 2.8.

It was was established in [BT, §9] that for $\beta =1/\alpha $ , there exists $c>0$ such that the following bound on the tails holds:

$$ \begin{align*} \mu_Y(\tau\ge n)\sim cn^{-\beta}. \end{align*} $$

That is, assumption (GM0) is fulfilled.

Note that if $\alpha \in (0, 1/2)$ , then $\beta> 2$ and if $\alpha \in (1/2,1)$ , then $\beta \in (1,2)$ .

Recall that assumption (GM1) is an assumption on the induced version of a potential $\psi $ . It states that there exists $\gamma \in (\beta -1, \beta )$ such that $\bar \psi =C_0 - \psi _0$ with $0 \leq \psi _0 \leq C_1 \tau ^{\gamma }$ . The last assumption in Theorem 2.8, besides assumptions (GM0) and (GM1), is that $q_1>3$ , which in particular implies that $\beta / \gamma>3$ . Under assumption (GM1), we have that $\beta / \gamma \in (1, \beta / (\beta -1))$ . Also, for $\beta>2$ , we have $\beta / (\beta -1)<2$ . Thus, if $\alpha \in (0, 1/2)$ , then the assumptions of Theorem 2.8 cannot be satisfied ( $q_1$ is always smaller than 3). However, for $\alpha \in (1/2, 1)$ , the result holds.

Proposition 7.1. The conclusions of Theorem 2.8 hold for the induced system $(T, \mu _Y)$ with $\alpha \in (1/2,1)$ and $\psi :[0,1] \to \mathbb {R}$ a Hölder function such that $\psi (x) = -x^{(1-\gamma )\alpha }$ for $\gamma \in ((1-\alpha )/\alpha , \alpha /(\alpha +1))$ , $\beta / \gamma>3$ and x in a neighbourhood of $0$ .

In the case $\beta>3$ , we can consider the case $\gamma =1$ in this setting. Here, we can for example choose $\psi $ to be Hölder and negative (bounded below by $-C_1$ ) in $Y^c$ and to be equal to $C_0$ and Theorem 2.8 holds.

Proof. We already established that assumption (GM0) is satisfied. It was proved in [BTT1, Proposition 8.5] that if $\gamma \in (0, \alpha / (\alpha +1))$ , then the induced potential satisfies $\bar \psi (x) \sim C-\tau (x)^\gamma $ as $x\to 1/2$ . Thus, the parameter $\gamma $ has to be chosen from the set $(\beta -1, \beta ) \cap (0, \alpha / (\alpha +1))$ so as $\beta / \gamma>3$ . These conditions are compatible, so we can assume that $q_1>3$ and that assumption (GM1) is fulfilled.

For the final statement, note that in this setting, $\bar \psi (x) = C_0-\psi _0(x)$ , where $0\le \psi _0(x) \le C_1\tau (x)$ .

Similarly, we obtain a version of Theorem 2.9 in the same range of values of $\alpha $ , but for a different range of values of $\gamma $ .

Proposition 7.2. The conclusions of Theorem 2.9 hold for the induced system $(T, \mu _Y)$ with $\alpha \in (1/2,1)$ and $\psi :[0,1] \to \mathbb {R}$ a function such that there exists $\gamma \in (\beta -1, 1)$ for which $\bar \psi = C_0-C_1 \tau ^{\gamma }$ . Both cases, $\beta /\gamma \in (1,2]$ and $\beta /\gamma \in (2,3)$ , occur.

In the case where $b=1$ , a construction to produce $\psi $ as above is given as follows. Let $x_0=1$ and $x_n=f_L^{-n}(1/2)$ , where $f_L$ is the left branch of f. Then, on the intervals $X_n:= (x_n, x_{n-1}]$ , define $\psi |_{X_1} = C_0-C_1$ and $\psi |_{X_n} =C_1(-n^\gamma +(n-1)^\gamma )$ , so for x having $\tau (x) = n$ , $\bar \psi = C_0+C_1\sum _{k=1}^n(-n^\gamma +(n-1)^\gamma ) = C_0 - C_1n^\gamma $ , as required.

Observe that for $\alpha \in (0, 1/2)$ , we have $\beta>2$ and for Theorem 2.9 to hold, we require $\beta \in (1,2)$ . Therefore, the appropriate range of values of $\alpha $ to apply our main results is $(1/2, 1)$ .

7.2 Suspensions over intermittent interval maps

In this section, we consider suspension flows over the induced map T defined in §7.1. Essentially, this is a continuous time representation of T that preserves its main properties. Let $\rho : Y \to \mathbb {R}^+$ be a Hölder function bounded away from zero. Let $\bar \tau : Y \to \mathbb {R}^+$ be defined by $\bar \tau (x)= \sum _{j=0}^{\tau (x)-1} \rho (f^j x)$ . Let $(F_t)_t$ be the suspension (semi)flow with base map T and roof function $\bar \tau $ . Since $\rho $ is bounded, assumption (GM0) is satisfied (as in §7.1) for the measure $\mu _Y$ .

A standard tool to construct examples in suspension flows is the following. Given a regular potential defined on the base space $g: Y \to \mathbb {R}$ , construct a continuous potential $\psi : Y^{\bar \tau } \to \mathbb {R}$ so that its induced version coincides with g, that is, $\bar \psi = g$ . Details of this type of construction can be found in [BRW], but minor adaptations are required in this setting. Since the assumptions of our main results are in terms of the induced potentials, this tool allows us to state flow versions of Propositions 7.1 and 7.2. Indeed, we just need to consider potentials $\psi : Y^{\bar \tau } \to \mathbb {R}$ so that its induced versions satisfy the properties of the induced potentials $\bar \psi $ in Propositions 7.1 and 7.2.