No CrossRef data available.
Article contents
Hyperbolic Lyapunov–Perron regular points and smooth invariant measures
Published online by Cambridge University Press: 17 June 2022
Abstract
For a 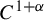 $C^{1+\alpha }$ diffeomorphism f of a compact smooth manifold, we give a necessary and sufficient condition that guarantees that if the set of hyperbolic Lyapunov–Perron regular points has positive volume, then f preserves a smooth measure. We use recent results on symbolic coding of
$C^{1+\alpha }$ diffeomorphism f of a compact smooth manifold, we give a necessary and sufficient condition that guarantees that if the set of hyperbolic Lyapunov–Perron regular points has positive volume, then f preserves a smooth measure. We use recent results on symbolic coding of 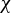 $\chi $-non-uniformly hyperbolic sets and results concerning the existence of SRB measures for them.
$\chi $-non-uniformly hyperbolic sets and results concerning the existence of SRB measures for them.
MSC classification
Secondary:
37D05: Hyperbolic orbits and sets
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
Alves, J. F., Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140(2) (2000), 351–98.10.1007/s002220000057CrossRefGoogle Scholar
Barreira, L. and Pesin, Y.. Nonuniform Hyperbolicity: Dynamics of Systems with Nonzero Lyapunov Exponents (Encyclopedia of Mathematics and Its Applications, 115). Cambridge University Press, Cambridge, 2007.10.1017/CBO9781107326026CrossRefGoogle Scholar
Ben Ovadia, S.. Symbolic dynamics for non-uniformly hyperbolic diffeomorphisms of compact smooth manifolds. J. Mod. Dyn. 13 (2018), 43–113.CrossRefGoogle Scholar
Ben Ovadia, S.. Hyperbolic SRB measures and the leaf condition. Comm. Math. Phys. 387 (2021), 1353–1404.CrossRefGoogle Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115(1) (2000), 157–193.10.1007/BF02810585CrossRefGoogle Scholar
Bowen, R. E.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470), 2nd edn. Ed. Chazottes, J.-R.. Springer-Verlag, Berlin, 2008.10.1007/978-3-540-77695-6CrossRefGoogle Scholar
Burns, K., Dolgopyat, D., Pesin, Y. and Pollicott, M.. Stable ergodicity for partially hyperbolic attractors with negative central exponents. J. Mod. Dyn. 2(1) (2008), 1–19.Google Scholar
Climenhaga, V., Dolgopyat, D. and Pesin, Y.. Non-stationary non-uniform hyperbolicity: SRB measures for dissipative maps. Comm. Math. Phys. 346(2) (2016), 553–602.10.1007/s00220-016-2710-zCrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms: part I: characterization of measures satisfying Pesin’s entropy formula. Ann. of Math. (2) 122(3) (1985), 509–39.10.2307/1971328CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms: part II: relations between entropy, exponents and dimension. Ann. of Math. (2) 122(3) (1985), 540–74.10.2307/1971329CrossRefGoogle Scholar
Pesin, Y. B. and Sinai, Y. G.. Gibbs measures for partially hyperbolic attractors. Ergod. Th. & Dynam. Sys. 2(3–4) (1982), 417–38.CrossRefGoogle Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A., Tahzibi, A. and Ures, R.. A criterion for ergodicity for non-uniformly hyperbolic diffeomorphisms. Electron. Res. Announc. Math. Sci. 14, (2007), 74.Google Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A., Tahzibi, A. and Ures, R.. Uniqueness of SRB measures for transitive diffeomorphisms on surfaces. Comm. Math. Phys. 306(1) (2011), 35–49.CrossRefGoogle Scholar
Ruelle, D.. A measure associated with Axiom-A attractors. Amer. J. Math. 98(3) (1976), 619–654.10.2307/2373810CrossRefGoogle Scholar
Sarig, O.. Symbolic dynamics for surface diffeomorphisms with positive entropy. J. Amer. Math. Soc. 26(2) (2013), 341–426.CrossRefGoogle Scholar
Sinai, Y. G.. Gibbs measures in ergodic theory. Russian Math. Surveys 27(4) (1972), 21–64.CrossRefGoogle Scholar
Tsujii, M.. Regular points for ergodic Sinai measures. Trans. Amer. Math. Soc. 328(2) (1991), 747–766.Google Scholar


