No CrossRef data available.
Article contents
Immediate conditional hyperbolicity in dynamical systems
Published online by Cambridge University Press: 19 September 2008
Abstract
For many diffeomorphisms of a compact manifold X, eventual conditional hyperbolicity implies immediate conditional hyperbolicity in some (possibly new) Finsler structures. That is, if A and B are vector bundle isomorphisms over the mapping ƒ of the base X, such that 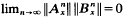 uniformly on X, then there exist new norms for A and B such that
uniformly on X, then there exist new norms for A and B such that 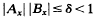 uniformly on X, whenever the mapping ƒ satisfies the condition that there exist infinitely many N ≥ 1 such that any ƒ-invariant. For example, this condition on ƒ holds if any one of the following conditions holds: (1) ƒ is periodic; (2) ƒ is periodic on its non-wandering set; (3) ƒ has a finite non-wandering set (for example, ƒ is a Morse-Smale diffeomorphism); (4) ƒ is an almost periodic mapping of a connected base X; (5) ƒ is a mapping of the circle with no periodic points; or (6) ƒ and all its powers are uniquely ergodic. We consider various types of eventually conditionally hyperbolic systems and describe sufficient conditions on ƒ to have immediate conditional hyperbolicity of these systems in some new Finsler structures. Thus, for a sizable class of dynamical systems, we settle, in the affirmative, a question raised by Hirsch, Pugh, and Shub.
uniformly on X, whenever the mapping ƒ satisfies the condition that there exist infinitely many N ≥ 1 such that any ƒ-invariant. For example, this condition on ƒ holds if any one of the following conditions holds: (1) ƒ is periodic; (2) ƒ is periodic on its non-wandering set; (3) ƒ has a finite non-wandering set (for example, ƒ is a Morse-Smale diffeomorphism); (4) ƒ is an almost periodic mapping of a connected base X; (5) ƒ is a mapping of the circle with no periodic points; or (6) ƒ and all its powers are uniquely ergodic. We consider various types of eventually conditionally hyperbolic systems and describe sufficient conditions on ƒ to have immediate conditional hyperbolicity of these systems in some new Finsler structures. Thus, for a sizable class of dynamical systems, we settle, in the affirmative, a question raised by Hirsch, Pugh, and Shub.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1983

