Article contents
Indiscriminate covers of infinite translation surfaces are innocent, not devious
Published online by Cambridge University Press: 04 December 2017
Abstract
We consider the interaction between passing to finite covers and ergodic properties of the straight-line flow on finite-area translation surfaces with infinite topological type. Infinite type provides for a rich family of degree-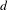 $d$ covers for any integer
$d$ covers for any integer  $d>1$. We give examples which demonstrate that passing to a finite cover can destroy ergodicity, but we also provide evidence that this phenomenon is rare. We define a natural notion of a random degree
$d>1$. We give examples which demonstrate that passing to a finite cover can destroy ergodicity, but we also provide evidence that this phenomenon is rare. We define a natural notion of a random degree 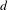 $d$ cover and show that, in many cases, ergodicity and unique ergodicity are preserved under passing to random covers. This work provides a new context for exploring the relationship between recurrence of the Teichmüller flow and ergodic properties of the straight-line flow.
$d$ cover and show that, in many cases, ergodicity and unique ergodicity are preserved under passing to random covers. This work provides a new context for exploring the relationship between recurrence of the Teichmüller flow and ergodic properties of the straight-line flow.
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 3
- Cited by

