Article contents
Inhomogeneous self-similar sets with overlaps
Published online by Cambridge University Press: 04 May 2017
Abstract
It is known that if the underlying iterated function system satisfies the open set condition, then the upper box dimension of an inhomogeneous self-similar set is the maximum of the upper box dimensions of the homogeneous counterpart and the condensation set. First, we prove that this ‘expected formula’ does not hold in general if there are overlaps in the construction. We demonstrate this via two different types of counterexample: the first is a family of overlapping inhomogeneous self-similar sets based upon Bernoulli convolutions; and the second applies in higher dimensions and makes use of a spectral gap property that holds for certain subgroups of 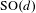 $\text{SO}(d)$ for
$\text{SO}(d)$ for  $d\geq 3$. We also obtain new upper bounds, derived using sumsets, for the upper box dimension of an inhomogeneous self-similar set which hold in general. Moreover, our counterexamples demonstrate that these bounds are optimal. In the final section we show that if the weak separation property is satisfied, that is, the overlaps are controllable, then the ‘expected formula’ does hold.
$d\geq 3$. We also obtain new upper bounds, derived using sumsets, for the upper box dimension of an inhomogeneous self-similar set which hold in general. Moreover, our counterexamples demonstrate that these bounds are optimal. In the final section we show that if the weak separation property is satisfied, that is, the overlaps are controllable, then the ‘expected formula’ does hold.
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 8
- Cited by

