No CrossRef data available.
Article contents
Interval projections of self-similar sets
Published online by Cambridge University Press: 14 June 2018
Abstract
We show if 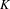 $K$ is a self-similar
$K$ is a self-similar  $1$-set that either satisfies the strong separation condition or is defined via homotheties then there are at most finitely many lines through the origin such that the projection of
$1$-set that either satisfies the strong separation condition or is defined via homotheties then there are at most finitely many lines through the origin such that the projection of 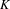 $K$ onto them is an interval.
$K$ onto them is an interval.
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2018
References
Besicovitch, A. S.. On the fundamental geometrical properties of linearly measurable plane sets of points (III). Math. Ann.
116 (1939), 349–357.Google Scholar
Falconer, K. and Fraser, J. M.. The visible part of plane self-similar sets. Proc. Amer. Math. Soc.
141 (2013), 269–278.10.1090/S0002-9939-2012-11312-7Google Scholar
Farkas, Á.. Projections of self-similar sets with no separation condition. Israel J. Math.
214 (2016), 67–107.Google Scholar
Federer, H.. The (𝜑, k) rectifiable subsets of n-space. Trans. Amer. Math. Soc.
62 (1947), 114–192.Google Scholar
Hutchinson, J. E.. Fractals and self-similarity. Indiana Univ. Math. J.
30 (1981), 713–747.Google Scholar
Kenyon, R.. Projecting the one-dimensional Sierpinski gasket. Israel J. Math.
97 (1997), 221–238.Google Scholar
Marstrand, J. M.. Some fundamental geometrical properties of plane sets of fractional dimensions. Proc. Lond. Math. Soc. (3)
4 (1954), 257–302.Google Scholar
Mattila, P.. Hausdorff dimension, orthogonal projections and intersections with planes. Ann. Acad. Sci. Fenn. Ser. A
1 (1975), 227–244.Google Scholar
Mattila, P.. Pertti On the structure of self-similar fractals. Ann. Acad. Sci. Fenn. Ser. A
7 (1982), 189–195.Google Scholar
Mattila, P.. Geometry of Sets and Measures in Euclidean Spaces. Cambridge University Press, Cambridge, 1995.Google Scholar
Schief, A.. Separation properties for self-similar sets. Proc. Amer. Math. Soc.
122 (1994), 111–115.10.1090/S0002-9939-1994-1191872-1Google Scholar
Wang, J. L.. The open set conditions for graph directed self-similar sets. Random Comput. Dynam.
5 (1997), 283–305.Google Scholar

