Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Amour, L
1993.
Inverse spectral theory for the AKNS system with separated boundary conditions.
Inverse Problems,
Vol. 9,
Issue. 5,
p.
507.
Gesztesy, F.
and
Weikard, R.
1993.
Differential Equations with Applications to Mathematical Physics.
Vol. 192,
Issue. ,
p.
101.
Vanini, Paolo
1994.
Mixed quantum mechanical periodic and potential wall problem.
Letters in Mathematical Physics,
Vol. 32,
Issue. 4,
p.
331.
Carlson, R
1994.
Inverse Sturm-Liouville problems with a singularity at zero.
Inverse Problems,
Vol. 10,
Issue. 4,
p.
851.
Amour, L.
and
Guillot, J. C.
1996.
Isospectral sets for akns systems on the unit interval with generalized periodic boundary conditions.
Geometric and Functional Analysis,
Vol. 6,
Issue. 1,
p.
1.
Gesztesy, F.
Simon, B.
and
Teschl, G.
1996.
Spectral deformations of one-dimensional Schrödinger operators.
Journal d'Analyse Mathématique,
Vol. 70,
Issue. 1,
p.
267.
Carlson, Robert
1997.
A Borg–Levinson theorem for Bessel operators.
Pacific Journal of Mathematics,
Vol. 177,
Issue. 1,
p.
1.
Caudill, Lester F.
Perry, Peter A.
and
Schueller, Albert W.
1998.
Isospectral Sets for Fourth-Order Ordinary Differential Operators.
SIAM Journal on Mathematical Analysis,
Vol. 29,
Issue. 4,
p.
935.
Amour, L.
2001.
Isospectral Flows of Third Order Operators.
SIAM Journal on Mathematical Analysis,
Vol. 32,
Issue. 6,
p.
1375.
Carlson, Robert
2004.
A Spectral Transform for the Matrix Hill's Equation.
Rocky Mountain Journal of Mathematics,
Vol. 34,
Issue. 3,
Binding, P.A.
and
Volkmer, H.
2006.
Interlacing and oscillation for Sturm–Liouville problems with separated and coupled boundary conditions.
Journal of Computational and Applied Mathematics,
Vol. 194,
Issue. 1,
p.
75.
Binding, P A
and
Volkmer, H
2007.
Inverse oscillation theory for Sturm–Liouville problems with non-separated boundary conditions.
Inverse Problems,
Vol. 23,
Issue. 1,
p.
343.
Koyunbakan, Hikmet
and
Panakhov, Etibar S.
2007.
Half-inverse problem for diffusion operators on the finite interval.
Journal of Mathematical Analysis and Applications,
Vol. 326,
Issue. 2,
p.
1024.
Amour, L
2009.
Explicit isospectral flows for the AKNS operator on the unit interval.
Inverse Problems,
Vol. 25,
Issue. 9,
p.
095008.
Damanik, David
Killip, Rowan
and
Simon, Barry
2010.
Perturbations of orthogonal polynomials with periodic recursion coefficients.
Annals of Mathematics,
Vol. 171,
Issue. 3,
p.
1931.
Amour, Laurent
2012.
Explicit isospectral flows associated to the AKNS operator on the unit interval. II.
Journal of Mathematical Physics,
Vol. 53,
Issue. 10,
Hantáková, Jana
and
Roth, Samuel
2021.
On backward attractors of interval maps*
.
Nonlinearity,
Vol. 34,
Issue. 11,
p.
7415.
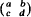 in SL(2, R) for the Sturm-Liouville equation on the unit interval. This is done by first studying the larger manifold M of all pairs of boundary conditions and potentials with a given spectrum and characterizing the critical points of the map from M to the trace a + d Isospectral sets appear as slices of M whose geometry is determined by the critical point structure of the trace function. This paper completes the classification of isospectral sets for all real self-adjoint boundary conditions.
in SL(2, R) for the Sturm-Liouville equation on the unit interval. This is done by first studying the larger manifold M of all pairs of boundary conditions and potentials with a given spectrum and characterizing the critical points of the map from M to the trace a + d Isospectral sets appear as slices of M whose geometry is determined by the critical point structure of the trace function. This paper completes the classification of isospectral sets for all real self-adjoint boundary conditions.
