Article contents
Joint ergodicity for group actions
Published online by Cambridge University Press: 19 September 2008
Abstract
Let T1,…,Tn be continuous representations of a σ-compact separable locally compact amenable group G as measure-preserving transformations of a non-atomic separable probability space (X, β, m). Let (Kn) be a right Følner sequence of compact sets in G. If T1,…,Tn are pairwise commuting in the sense that Ti(g)Tj(h) = Tj(h)Ti(g) for i ≠ j and g, h ∈ G, then necessary and sufficient conditions can be given, in terms of the ergodicity of certain tensor products, for the following to hold: for all F1,…,Fn∈L∞, the sequence AN(x) where
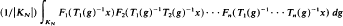
converges in L2(X) to 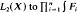 . The necessary and sufficient conditions are that each of the following representations are ergodic: Tn, Tn−1⊗Tn−1Tn,…,T2⊗T2T3⊗…⊗T2…Tn, T1⊗T1T2⊗…⊗T1…Tn.
. The necessary and sufficient conditions are that each of the following representations are ergodic: Tn, Tn−1⊗Tn−1Tn,…,T2⊗T2T3⊗…⊗T2…Tn, T1⊗T1T2⊗…⊗T1…Tn.
In order to prove this theorem, specific properties of the decomposition of L2(X) into its weakly mixing and compact subspaces with respect to a representation Ti are needed. These properties are also used to prove some generalizations of wellknown facts from ergodic theory in the case where G is the integer group Z.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1988
References
REFERENCES
- 5
- Cited by

