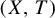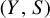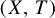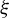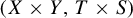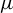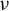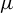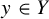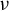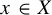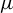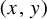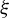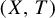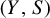1. Introduction
All terminology used freely in this introduction is explained in the preliminaries (§2).
Let
![]() $\pi :(X,T) \rightarrow (Y,S)$
be an extension of a compact dynamical system
$\pi :(X,T) \rightarrow (Y,S)$
be an extension of a compact dynamical system
![]() $(Y,S)$
and suppose that
$(Y,S)$
and suppose that
![]() $\nu $
is an ergodic measure for S. This measure can always be lifted to an invariant measure on X (by the Hahn–Banach theorem). It then follows that there exists an ergodic measure
$\nu $
is an ergodic measure for S. This measure can always be lifted to an invariant measure on X (by the Hahn–Banach theorem). It then follows that there exists an ergodic measure
![]() $\mu $
that projects to
$\mu $
that projects to
![]() $\nu $
. Clearly, any generic point for
$\nu $
. Clearly, any generic point for
![]() $\mu $
will project to a generic point for
$\mu $
will project to a generic point for
![]() $\nu $
. It is natural to ask whether all
$\nu $
. It is natural to ask whether all
![]() $\nu $
-generic points can be obtained in this way. In other words: does every
$\nu $
-generic points can be obtained in this way. In other words: does every
![]() $\nu $
-generic point have a
$\nu $
-generic point have a
![]() $\mu $
-generic lift? It is not difficult to show that if
$\mu $
-generic lift? It is not difficult to show that if
![]() $\mu $
is a unique lift of
$\mu $
is a unique lift of
![]() $\nu $
then the answer is yes. In fact, in this case if
$\nu $
then the answer is yes. In fact, in this case if
![]() $y \in Y$
is generic for
$y \in Y$
is generic for
![]() $\nu $
then any
$\nu $
then any
![]() $x\in \pi ^{-1}(y)$
will be generic for
$x\in \pi ^{-1}(y)$
will be generic for
![]() $\mu $
. However, if the extension of
$\mu $
. However, if the extension of
![]() $\nu $
is not unique then the answer might be negative. Such examples can be obtained as follows.
$\nu $
is not unique then the answer might be negative. Such examples can be obtained as follows.
Consider a minimal almost one-to-one extension
![]() $\pi :X \rightarrow Y$
where Y is strictly ergodic but X is not (cf. Furstenberg and Weiss [Reference Furstenberg and WeissFW] for examples of such systems). Then all invariant measures on X project to the unique measure
$\pi :X \rightarrow Y$
where Y is strictly ergodic but X is not (cf. Furstenberg and Weiss [Reference Furstenberg and WeissFW] for examples of such systems). Then all invariant measures on X project to the unique measure
![]() $\nu $
on Y. In this situation all points in Y are generic for
$\nu $
on Y. In this situation all points in Y are generic for
![]() $\nu $
. Now, let
$\nu $
. Now, let
![]() $y\in Y$
be a point with a unique preimage
$y\in Y$
be a point with a unique preimage
![]() $x\in X$
(by assumption such a point exists). Then either x is not generic for any invariant measure on X or it is generic for one such measure (say,
$x\in X$
(by assumption such a point exists). Then either x is not generic for any invariant measure on X or it is generic for one such measure (say,
![]() $\mu _0$
). In either case, there exists an invariant measure
$\mu _0$
). In either case, there exists an invariant measure
![]() $\mu _1$
on X such that x is not generic for
$\mu _1$
on X such that x is not generic for
![]() $\mu _1$
. Thus, the point y generic for
$\mu _1$
. Thus, the point y generic for
![]() $\nu $
does not lift to a point generic for the lift
$\nu $
does not lift to a point generic for the lift
![]() $\mu _1$
of
$\mu _1$
of
![]() $\nu $
.
$\nu $
.
However, this example does not provide an answer to a more subtle question: does every
![]() $\nu $
-generic point have a generic lift (without specifying for which measure extending
$\nu $
-generic point have a generic lift (without specifying for which measure extending
![]() $\nu $
)? In general, the answer to such a relaxed question is also negative. We will show this using the same example as before and the following theorem.
$\nu $
)? In general, the answer to such a relaxed question is also negative. We will show this using the same example as before and the following theorem.
Theorem 1.1. Let
![]() $(X,T)$
be a topological dynamical system with (at least) two different ergodic measures
$(X,T)$
be a topological dynamical system with (at least) two different ergodic measures
![]() $\mu $
and
$\mu $
and
![]() $\nu $
, both having full topological support. Then there exist a dense
$\nu $
, both having full topological support. Then there exist a dense
![]() $G_{\delta }$
-set
$G_{\delta }$
-set
![]() $B\subset X$
and a continuous function f on X such that for any
$B\subset X$
and a continuous function f on X such that for any
![]() $x\in B$
the ergodic averages
$x\in B$
the ergodic averages
 $$ \begin{align*} A_n(f,x)=\frac1n\sum_{i=0}^{n-1}f(T^ix) \end{align*} $$
$$ \begin{align*} A_n(f,x)=\frac1n\sum_{i=0}^{n-1}f(T^ix) \end{align*} $$
oscillate.
Proof. Since the measures differ, there exists a continuous function f on X whose integral with respect to
![]() $\mu $
is greater than one while its integral with respect to
$\mu $
is greater than one while its integral with respect to
![]() $\nu $
is less than zero. Now, for a natural number N we define
$\nu $
is less than zero. Now, for a natural number N we define
 $$ \begin{align*} E_N = \bigg\{ x \in X :\text{ there exists }_{n> N}\ \frac{1}n\sum_{i=0}^{n-1} f(T^ix) > 1\bigg\}. \end{align*} $$
$$ \begin{align*} E_N = \bigg\{ x \in X :\text{ there exists }_{n> N}\ \frac{1}n\sum_{i=0}^{n-1} f(T^ix) > 1\bigg\}. \end{align*} $$
This set is clearly open, and it is dense since the generic points for
![]() $\mu $
are dense. Define a similar set
$\mu $
are dense. Define a similar set
![]() $F_N$
replacing ‘
$F_N$
replacing ‘
![]() $>1$
’ by ‘
$>1$
’ by ‘
![]() $<0$
’. Then the desired set B is the countable intersection
$<0$
’. Then the desired set B is the countable intersection
By the Baire theorem, this set is a dense
![]() $G_\delta $
, and clearly no
$G_\delta $
, and clearly no
![]() $x\in B$
is generic for any measure.
$x\in B$
is generic for any measure.
Now let us go back to the example. Since the system
![]() $(X,T)$
is minimal, all its invariant measures have full topological support. By Theorem 1.1, there is a dense
$(X,T)$
is minimal, all its invariant measures have full topological support. By Theorem 1.1, there is a dense
![]() $G_\delta $
-set B of points which are not generic for any measure. As in any minimal almost one-to-one extension, the ‘singleton fibers’ (that is, points which are unique preimages of their images) also form a dense
$G_\delta $
-set B of points which are not generic for any measure. As in any minimal almost one-to-one extension, the ‘singleton fibers’ (that is, points which are unique preimages of their images) also form a dense
![]() $G_\delta $
-set (call it A) in X. Then the intersection
$G_\delta $
-set (call it A) in X. Then the intersection
![]() $A\cap B$
is non-empty and any point in its image is generic (for
$A\cap B$
is non-empty and any point in its image is generic (for
![]() $\nu $
) but has no generic lift.
$\nu $
) but has no generic lift.
An even more extreme situation occurs in yet another example. In [Reference FurstenbergF], Furstenberg constructs a non-uniquely ergodic minimal skew product on the
![]() $2$
-torus over an irrational rotation, where the fiber maps are also rotations. Since rotation by a fixed angle on the fibers commutes with the skew product, in every fiber either each point is generic for some invariant measure or none of them is. Theorem 1.1 implies that there are points not generic for any measure (actually, this property is explicit in [Reference FurstenbergF]—this is how Furstenberg showed non-unique ergodicity of the skew product). It follows that there are entire fibers (circles) with no generic points even though in the base all points are generic.
$2$
-torus over an irrational rotation, where the fiber maps are also rotations. Since rotation by a fixed angle on the fibers commutes with the skew product, in every fiber either each point is generic for some invariant measure or none of them is. Theorem 1.1 implies that there are points not generic for any measure (actually, this property is explicit in [Reference FurstenbergF]—this is how Furstenberg showed non-unique ergodicity of the skew product). It follows that there are entire fibers (circles) with no generic points even though in the base all points are generic.
Before we discuss a positive result we need to mention two important issues. The first one is the phenomenon of quasi-generating invariant measures, that is, generating them along a subsequence of averages. Replacing the term ‘generic’ by ‘quasi-generic’ may lead to either stronger or weaker results, depending on where the replacement is done (in the assumption or in the thesis). The second issue is a specific way of extending a system by joining it with another system. Any extension can be viewed practically as a joining of the system with its extension (the joining is then supported by the graph of the factor map), but it is often essential to know that the extension can be obtained as a joining with a system having some specific properties (ergodicity, specification property, etc.) which the entire extension does not necessarily enjoy.
In the early 1970s, Teturo Kamae studied normal sequences and the phenomenon of normality-preserving subsequences. In symbolic dynamics a sequence over a finite alphabet is normal if it is generic for the uniform Bernoulli measure. An increasing subsequence of natural numbers
![]() $y=(n_k)_{k\ge 1}$
preserves normality if
$y=(n_k)_{k\ge 1}$
preserves normality if
![]() $x|_y=(x_{n_k})_{k\ge 1}$
is normal for any normal sequence
$x|_y=(x_{n_k})_{k\ge 1}$
is normal for any normal sequence
![]() $(x_n)_{n\ge 1}$
. A few years earlier, Weiss [Reference WeissW] proved that subsequences of positive lower density which are completely deterministic preserve normality. A subsequence y is completely deterministic if its indicator function, viewed as an element of the shift on two symbols, quasi-generates only measures of entropy zero. Kamae [Reference KamaeK] proved the opposite implication: only completely deterministic subsequences preserve normality. Given a non-deterministic subsequence y (that is, one that quasi-generates some measure
$(x_n)_{n\ge 1}$
. A few years earlier, Weiss [Reference WeissW] proved that subsequences of positive lower density which are completely deterministic preserve normality. A subsequence y is completely deterministic if its indicator function, viewed as an element of the shift on two symbols, quasi-generates only measures of entropy zero. Kamae [Reference KamaeK] proved the opposite implication: only completely deterministic subsequences preserve normality. Given a non-deterministic subsequence y (that is, one that quasi-generates some measure
![]() $\nu $
of positive entropy), he needed to find a normal sequence x such that
$\nu $
of positive entropy), he needed to find a normal sequence x such that
![]() $x|_y$
is not normal. Skipping the details, let us just say that he needed to ‘pair’ the subsequence y with a normal (that is, generic for the uniform Bernoulli measure
$x|_y$
is not normal. Skipping the details, let us just say that he needed to ‘pair’ the subsequence y with a normal (that is, generic for the uniform Bernoulli measure
![]() $\unicode{x3bb} $
) sequence x, such that the pair
$\unicode{x3bb} $
) sequence x, such that the pair
![]() $(x,y)$
is generic for a specific joining
$(x,y)$
is generic for a specific joining
![]() $\xi $
of
$\xi $
of
![]() $\unicode{x3bb} $
and
$\unicode{x3bb} $
and
![]() $\nu $
. In order to do so, he proved a more general theorem, which motivates our current work. We take the liberty of rephrasing the statement in the language that we use throughout this paper.
$\nu $
. In order to do so, he proved a more general theorem, which motivates our current work. We take the liberty of rephrasing the statement in the language that we use throughout this paper.
Theorem 1.2. [Reference KamaeK]
Let
![]() $\xi $
be a joining of two invariant measures,
$\xi $
be a joining of two invariant measures,
![]() $\mu $
and
$\mu $
and
![]() $\nu $
, supported on symbolic systems
$\nu $
, supported on symbolic systems
![]() $\Lambda _1^{\mathbb {N}}$
and
$\Lambda _1^{\mathbb {N}}$
and
![]() $\Lambda _2^{\mathbb {N}}$
, respectively (
$\Lambda _2^{\mathbb {N}}$
, respectively (
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
are finite alphabets). Let
$\Lambda _2$
are finite alphabets). Let
![]() $y\in \Lambda _2^{\mathbb {N}}$
be quasi-generic for
$y\in \Lambda _2^{\mathbb {N}}$
be quasi-generic for
![]() $\nu $
, that is, it generates
$\nu $
, that is, it generates
![]() $\nu $
along a subsequence of averages indexed by
$\nu $
along a subsequence of averages indexed by
![]() $\mathcal J=(n_k)_{k\ge 1}$
. Then there exists
$\mathcal J=(n_k)_{k\ge 1}$
. Then there exists
![]() $x\in \Lambda _1^{\mathbb {N}}$
such that the pair
$x\in \Lambda _1^{\mathbb {N}}$
such that the pair
![]() $(x,y)$
generates
$(x,y)$
generates
![]() $\xi $
along
$\xi $
along
![]() $\mathcal J$
. If
$\mathcal J$
. If
![]() $\mu $
is ergodic then x can be chosen generic for
$\mu $
is ergodic then x can be chosen generic for
![]() $\mu $
.
$\mu $
.
This theorem found another application in the work of Rauzy [Reference RauzyR], who studied normality preservation in a different sense. Let us identify all real numbers with their expansions in some fixed base
![]() $b\ge 2$
. A real number is called normal (in base b) if its expansion is a normal sequence. A real number y preserves normality if
$b\ge 2$
. A real number is called normal (in base b) if its expansion is a normal sequence. A real number y preserves normality if
![]() $x+y$
is normal for any normal number x. Rauzy proved that a number y preserves normality if and only if the expansion of y is completely deterministic.
$x+y$
is normal for any normal number x. Rauzy proved that a number y preserves normality if and only if the expansion of y is completely deterministic.
Notice that Theorem 1.2 is actually very strong. First of all, it applies to any situation when a ‘symbolic’ measure
![]() $\nu $
is lifted to a ‘symbolic’ measure
$\nu $
is lifted to a ‘symbolic’ measure
![]() $\xi $
. Also note that
$\xi $
. Also note that
![]() $\nu $
is not assumed ergodic, it suffices that it admits a quasi-generic point y (which is always true within a full shift). If
$\nu $
is not assumed ergodic, it suffices that it admits a quasi-generic point y (which is always true within a full shift). If
![]() $\mathcal J={\mathbb {N}}$
then y is simply generic for
$\mathcal J={\mathbb {N}}$
then y is simply generic for
![]() $\nu $
and the theorem allows it to be lifted to a pair
$\nu $
and the theorem allows it to be lifted to a pair
![]() $(x,y)$
generic for
$(x,y)$
generic for
![]() $\xi $
. Even when
$\xi $
. Even when
![]() $\mathcal J$
is an essential subsequence (and there is no hope of making the lift
$\mathcal J$
is an essential subsequence (and there is no hope of making the lift
![]() $(x,y)$
generic), as soon as
$(x,y)$
generic), as soon as
![]() $\mu $
is ergodic, the point x ‘paired’ with y still can be generic rather than just quasi-generic. The only weakness of the theorem is that x is found within the full shift
$\mu $
is ergodic, the point x ‘paired’ with y still can be generic rather than just quasi-generic. The only weakness of the theorem is that x is found within the full shift
![]() $\Lambda _1^{\mathbb {N}}$
, even when
$\Lambda _1^{\mathbb {N}}$
, even when
![]() $\mu $
is supported by a proper subshift. In other words, the theorem does not allow y to be lifted within an a priori given topological (symbolic) extension.
$\mu $
is supported by a proper subshift. In other words, the theorem does not allow y to be lifted within an a priori given topological (symbolic) extension.
Our paper focuses exactly on this problem. Our goal is to find conditions under which the ‘paired’ point x (generic for
![]() $\mu $
) can be found within the a priori given topological system
$\mu $
) can be found within the a priori given topological system
![]() $(X,T)$
being joined with
$(X,T)$
being joined with
![]() $(Y,S)$
. The conditions turn out to be ergodicity of
$(Y,S)$
. The conditions turn out to be ergodicity of
![]() $\mu $
(like in the original theorem), and the weak specification property of
$\mu $
(like in the original theorem), and the weak specification property of
![]() $(X,T)$
. We prove the following theorem.
$(X,T)$
. We prove the following theorem.
Theorem 1.3. Let
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y,S)$
be topological dynamical systems and let
$(Y,S)$
be topological dynamical systems and let
![]() $\xi $
be an invariant measure on the product system
$\xi $
be an invariant measure on the product system
![]() $(X\times Y,T\times S)$
with marginals
$(X\times Y,T\times S)$
with marginals
![]() $\mu $
and
$\mu $
and
![]() $\nu $
on X and Y, respectively. Assume that the system
$\nu $
on X and Y, respectively. Assume that the system
![]() $(X,T)$
has the weak specification property and that
$(X,T)$
has the weak specification property and that
![]() $\mu $
is ergodic under T. Suppose also that
$\mu $
is ergodic under T. Suppose also that
![]() $y\in Y$
is quasi-generic for the measure
$y\in Y$
is quasi-generic for the measure
![]() $\nu $
. Then there exists a point
$\nu $
. Then there exists a point
![]() $x\in X$
, generic for
$x\in X$
, generic for
![]() $\mu $
, such that the pair
$\mu $
, such that the pair
![]() $(x,y)$
is quasi-generic for
$(x,y)$
is quasi-generic for
![]() $\xi $
.
$\xi $
.
Let us mention that the weak specification property is satisfied by many systems such as ergodic mixing Markov shifts, ergodic toral automorphisms, and in fact any endomorphisms of compact Abelian groups for which the Haar measure is ergodic (see [Reference DateyamaD] and use natural extension). An advantage of our result is that it is not restricted to symbolic systems and that x is found within the space X. A disadvantage is that the pair
![]() $(x,y)$
is only quasi-generic for
$(x,y)$
is only quasi-generic for
![]() $\xi $
, even when
$\xi $
, even when
![]() $\mathcal J={\mathbb {N}}$
.
$\mathcal J={\mathbb {N}}$
.
The strength of Theorem 1.3 lies in the possibility of lifting any generic point (not just almost any) y to a pair
![]() $(x,y)$
quasi-generic for
$(x,y)$
quasi-generic for
![]() $\xi $
. If
$\xi $
. If
![]() $\xi $
is ergodic, such a possibility for
$\xi $
is ergodic, such a possibility for
![]() $\nu $
-almost all y is a trivial fact. Thus, the theorem can be useful when topological, rather than measure-theoretic, precision is required.
$\nu $
-almost all y is a trivial fact. Thus, the theorem can be useful when topological, rather than measure-theoretic, precision is required.
A concrete application of Theorem 1.3 occurs in the forthcoming paper [Reference Bergelson and DownarowiczBD], where Rauzy’s equivalence between normality preservation and determinism is generalized to a wider context. That is to say, the following problem is addressed.
Question 1.4. Let
![]() $T:X\to X$
be a surjective endomorphism of a compact metrizable Abelian group, such that the Haar measure
$T:X\to X$
be a surjective endomorphism of a compact metrizable Abelian group, such that the Haar measure
![]() $\unicode{x3bb} $
on X is T-ergodic and has finite entropy. Let us call a point
$\unicode{x3bb} $
on X is T-ergodic and has finite entropy. Let us call a point
![]() $x\in X$
normal if it is generic for
$x\in X$
normal if it is generic for
![]() $\unicode{x3bb} $
. Is it true that y preserves normality (that is,
$\unicode{x3bb} $
. Is it true that y preserves normality (that is,
![]() $x+y$
is normal for any normal
$x+y$
is normal for any normal
![]() $x\in X$
) if and only if y is completely deterministic?
$x\in X$
) if and only if y is completely deterministic?
In [Reference Bergelson and DownarowiczBD] we prove sufficiency relatively easily, but the harder direction (necessity) is shown only for selected groups X (tori, solenoids, and countable direct products
![]() $\bigoplus _{n\ge 1}\mathbb Z_d$
(
$\bigoplus _{n\ge 1}\mathbb Z_d$
(
![]() $d\ge 2$
); the necessity in full generality remains open). In all these cases Theorem 1.3 plays a crucial role in the proofs.
$d\ge 2$
); the necessity in full generality remains open). In all these cases Theorem 1.3 plays a crucial role in the proofs.
Our paper is organized as follows. Section 2 contains all necessary definitions and notational conventions. In §3 we provide three key lemmas together with auxiliary propositions needed in their proofs. The propositions are quite standard while the lemmas may be considered of independent interest. Finally, in §4 we present the proof of Theorem 1.3.
2. Preliminaries
Let
![]() $(X,T)$
be a topological dynamical system, where X is a compact metric space and T is a continuous surjection. By
$(X,T)$
be a topological dynamical system, where X is a compact metric space and T is a continuous surjection. By
![]() $\mathcal M(X)$
we will denote the set of all Borel probability measures on X. Since no other measures will be considered, the elements of
$\mathcal M(X)$
we will denote the set of all Borel probability measures on X. Since no other measures will be considered, the elements of
![]() $\mathcal M(X)$
will be called measures for short. By
$\mathcal M(X)$
will be called measures for short. By
![]() $\mathcal M_T(X)$
we will denote the subset of
$\mathcal M_T(X)$
we will denote the subset of
![]() $\mathcal M(X)$
containing all measures that are T-invariant, that is, such that
$\mathcal M(X)$
containing all measures that are T-invariant, that is, such that
![]() $\mu (T^{-1}A)=\mu (A)$
for all Borel sets
$\mu (T^{-1}A)=\mu (A)$
for all Borel sets
![]() $A\subset X$
. When the transformation T is fixed, the elements of
$A\subset X$
. When the transformation T is fixed, the elements of
![]() $\mathcal M_T(X)$
will be called invariant measures. The sets
$\mathcal M_T(X)$
will be called invariant measures. The sets
![]() $\mathcal M(X)$
and
$\mathcal M(X)$
and
![]() $\mathcal M_T(X)$
are equipped with the weak* topology, which makes both these sets compact convex and metrizable with a convex metric. (By definition, a sequence
$\mathcal M_T(X)$
are equipped with the weak* topology, which makes both these sets compact convex and metrizable with a convex metric. (By definition, a sequence
![]() $(\mu _n)_{n\ge 1}$
of measures converges in the weak* topology to a measure
$(\mu _n)_{n\ge 1}$
of measures converges in the weak* topology to a measure
![]() $\mu $
if, for any continuous (real or complex) function f on X, the integrals
$\mu $
if, for any continuous (real or complex) function f on X, the integrals
![]() $\int f\,d\mu _n$
converge to
$\int f\,d\mu _n$
converge to
![]() $\int f\,d\mu $
. One of the standard convex metrics compatible with this topology is given by
$\int f\,d\mu $
. One of the standard convex metrics compatible with this topology is given by
 $$ \begin{align*} d(\mu,\nu)=\sum_{n=1}^\infty 2^{-n}\bigg|\int f_n\,d\mu - \int f_n\,d\nu\bigg|, \end{align*} $$
$$ \begin{align*} d(\mu,\nu)=\sum_{n=1}^\infty 2^{-n}\bigg|\int f_n\,d\mu - \int f_n\,d\nu\bigg|, \end{align*} $$
where
![]() $(f_n)_{n\ge 1}$
is a sequence of continuous functions on X with values in the interval
$(f_n)_{n\ge 1}$
is a sequence of continuous functions on X with values in the interval
![]() $[0,1]$
, linearly dense in the space
$[0,1]$
, linearly dense in the space
![]() $C(X)$
of all continuous real functions on X.) It is well known that the extreme points of
$C(X)$
of all continuous real functions on X.) It is well known that the extreme points of
![]() $\mathcal M_T(X)$
are precisely the ergodic measures, that is, invariant measures
$\mathcal M_T(X)$
are precisely the ergodic measures, that is, invariant measures
![]() $\mu $
such that
$\mu $
such that
![]() $\mu (A\,\triangle \, T^{-1}A)=0\! \implies \! \mu (A)\in \{0,1\}$
, for any Borel set
$\mu (A\,\triangle \, T^{-1}A)=0\! \implies \! \mu (A)\in \{0,1\}$
, for any Borel set
![]() $A\subset X$
.
$A\subset X$
.
We will be using the following notation. For two integers
![]() $a\le b$
, we will denote by
$a\le b$
, we will denote by
![]() $[a,b]$
the interval of integers
$[a,b]$
the interval of integers
![]() $\{a,a+1,a+2,\ldots ,b\}$
. Given a point
$\{a,a+1,a+2,\ldots ,b\}$
. Given a point
![]() $x\in X$
and
$x\in X$
and
![]() $0\le a\le b$
, we denote by
$0\le a\le b$
, we denote by
![]() $x[a,b]$
the ordered finite segment of the orbit of x,
$x[a,b]$
the ordered finite segment of the orbit of x,
while by
![]() $\mu _{x[a,b]}$
we will understand the normalized counting measure on
$\mu _{x[a,b]}$
we will understand the normalized counting measure on
![]() $x[a,b]$
,
$x[a,b]$
,
 $$ \begin{align*} \mu_{x[a,b]}=\frac1{b-a+1}\sum_{n=a}^b\delta_{T^nx} \end{align*} $$
$$ \begin{align*} \mu_{x[a,b]}=\frac1{b-a+1}\sum_{n=a}^b\delta_{T^nx} \end{align*} $$
(here
![]() $\delta _x$
denotes the Dirac measure concentrated at x). We will call this measure the empirical measure associated with the orbit segment.
$\delta _x$
denotes the Dirac measure concentrated at x). We will call this measure the empirical measure associated with the orbit segment.
A point x is said to quasi-generate (or be quasi-generic for) a measure
![]() $\mu $
if
$\mu $
if
![]() $\mu $
is an accumulation point of the sequence of measures
$\mu $
is an accumulation point of the sequence of measures
![]() $(\mu _{x[0,n]})_{n\ge 1}$
(any such measure
$(\mu _{x[0,n]})_{n\ge 1}$
(any such measure
![]() $\mu $
is invariant). In this case there exists an increasing sequence of natural numbers
$\mu $
is invariant). In this case there exists an increasing sequence of natural numbers
![]() $\mathcal J=(n_k)_{k\ge 1}$
such that
$\mathcal J=(n_k)_{k\ge 1}$
such that
![]() $\lim _{k\to \infty }\mu _{x[0,n_k]}=\mu $
. We will say that x generates
$\lim _{k\to \infty }\mu _{x[0,n_k]}=\mu $
. We will say that x generates
![]() $\mu $
along
$\mu $
along
![]() $\mathcal J$
. If the sequence
$\mathcal J$
. If the sequence
![]() $(\mu _{x[0,n]})_{n\ge 1}$
converges to
$(\mu _{x[0,n]})_{n\ge 1}$
converges to
![]() $\mu $
then we say that x generates (or is generic for)
$\mu $
then we say that x generates (or is generic for)
![]() $\mu $
(in other words, ‘generic’ equates to ‘generic along
$\mu $
(in other words, ‘generic’ equates to ‘generic along
![]() ${\mathbb {N}}$
’). It follows from the pointwise ergodic theorem that every ergodic measure
${\mathbb {N}}$
’). It follows from the pointwise ergodic theorem that every ergodic measure
![]() $\mu $
possesses generic points (in fact
$\mu $
possesses generic points (in fact
![]() $\mu $
-almost all points are such). The following obvious fact will be used several times.
$\mu $
-almost all points are such). The following obvious fact will be used several times.
Remark 2.1. Two increasing sequences of natural numbers (say,
![]() $(n_k)_{k\ge 1}$
and
$(n_k)_{k\ge 1}$
and
![]() $(m_k)_{k\ge 1}$
) will be called equivalent if
$(m_k)_{k\ge 1}$
) will be called equivalent if
![]() $\lim _{k\to \infty }({n_k}/{m_k})=1$
. It is obvious that the upper (and lower) densities of any subset of
$\lim _{k\to \infty }({n_k}/{m_k})=1$
. It is obvious that the upper (and lower) densities of any subset of
![]() ${\mathbb {N}}$
evaluated along equivalent sequences are the same. If a point x generates a measure
${\mathbb {N}}$
evaluated along equivalent sequences are the same. If a point x generates a measure
![]() $\mu $
along a sequence
$\mu $
along a sequence
![]() $(n_k)_{k\ge 1}$
then it generates
$(n_k)_{k\ge 1}$
then it generates
![]() $\mu $
along any sequence
$\mu $
along any sequence
![]() $(m_k)_{k\ge 1}$
equivalent to
$(m_k)_{k\ge 1}$
equivalent to
![]() $(n_k)_{k\ge 1}$
.
$(n_k)_{k\ge 1}$
.
Other key notions in this paper are those of a specification and the specification property.
Definition 2.2
-
(1) Consider a (finite or infinite) sequence of non-negative integers:
Let $$ \begin{align*} a_1\le &\,b_1<a_2\le b_2<\cdots<a_{N_1}\le b_{N_1} \quad \text{where } N_1\in{\mathbb{N}}, \text{ or }\\ a_1\le &\,b_1<a_2\le b_2<a_3\le b_3<\cdots\,. \end{align*} $$
$$ \begin{align*} a_1\le &\,b_1<a_2\le b_2<\cdots<a_{N_1}\le b_{N_1} \quad \text{where } N_1\in{\mathbb{N}}, \text{ or }\\ a_1\le &\,b_1<a_2\le b_2<a_3\le b_3<\cdots\,. \end{align*} $$
 $D=\bigcup _N[a_N,b_N]$
(where N ranges over either
$D=\bigcup _N[a_N,b_N]$
(where N ranges over either
 $[1,N_1]$
or
$[1,N_1]$
or
 ${\mathbb {N}}$
). By a specification with domain D we will mean any function such that for each N there exists a point
${\mathbb {N}}$
). By a specification with domain D we will mean any function such that for each N there exists a point $$ \begin{align*} {\mathcal S}:D\to X \end{align*} $$
$$ \begin{align*} {\mathcal S}:D\to X \end{align*} $$
 $x_N$
such that for each
$x_N$
such that for each
 $n\in [a_N,b_N]$
we have Since T is surjective, we can equivalently demand that
$n\in [a_N,b_N]$
we have Since T is surjective, we can equivalently demand that $$ \begin{align*} {\mathcal S}(n) = T^n(x_N). \end{align*} $$
$$ \begin{align*} {\mathcal S}(n) = T^n(x_N). \end{align*} $$
 ${\mathcal S}(n)=T^{n-a_N}(x_N)$
.
${\mathcal S}(n)=T^{n-a_N}(x_N)$
.
-
(2) By
 ${\mathcal S}[a_N,b_N]$
we mean the ordered tuple
${\mathcal S}[a_N,b_N]$
we mean the ordered tuple
 $({\mathcal S}(a_N),{\mathcal S}(a_N+1),\ldots ,{\mathcal S}(b_N))$
which equals
$({\mathcal S}(a_N),{\mathcal S}(a_N+1),\ldots ,{\mathcal S}(b_N))$
which equals
 $x_N[a_N,b_N]$
(or
$x_N[a_N,b_N]$
(or
 $x_N[0,b_N-a_N])$
.
$x_N[0,b_N-a_N])$
. -
(3) The numbers
 $l_N=b_N-a_N+1$
and
$l_N=b_N-a_N+1$
and
 $g_N=a_{N+1}-b_N-1$
will be called the orbit segment lengths and gaps of the specification, respectively.
$g_N=a_{N+1}-b_N-1$
will be called the orbit segment lengths and gaps of the specification, respectively. -
(4) If D is finite then the empirical measure associated with
 ${\mathcal S}$
is defined as
${\mathcal S}$
is defined as  $$ \begin{align*} \mu_{\mathcal S}=\frac1{|D|}\sum_{n\in D}\delta_{{\mathcal S}(n)}. \end{align*} $$
$$ \begin{align*} \mu_{\mathcal S}=\frac1{|D|}\sum_{n\in D}\delta_{{\mathcal S}(n)}. \end{align*} $$
-
(5) An infinite specification
 ${\mathcal S}$
generates (or is generic for) a measure
${\mathcal S}$
generates (or is generic for) a measure
 $\mu $
along a sequence
$\mu $
along a sequence
 $\mathcal J=(n_k)_{k\ge 1}$
if the measures associated to the specification
$\mathcal J=(n_k)_{k\ge 1}$
if the measures associated to the specification
 ${\mathcal S}$
restricted to
${\mathcal S}$
restricted to
 $D\cap [0,n_k]$
converge to
$D\cap [0,n_k]$
converge to
 $\mu $
(in general,
$\mu $
(in general,
 $\mu $
need not be invariant).
$\mu $
need not be invariant). -
(6) We say that (the orbit of) a point
 $x\in X \varepsilon $
-shadows the specification
$x\in X \varepsilon $
-shadows the specification
 ${\mathcal S}$
if
${\mathcal S}$
if  $$ \begin{align*} \text{for all }{n\in D},\quad d({\mathcal S}(n),T^n(x))<\varepsilon. \end{align*} $$
$$ \begin{align*} \text{for all }{n\in D},\quad d({\mathcal S}(n),T^n(x))<\varepsilon. \end{align*} $$
-
(7) A system
 $(X,T)$
has the weak specification property if for every
$(X,T)$
has the weak specification property if for every
 $\varepsilon>0$
there exists a function
$\varepsilon>0$
there exists a function
 $M_\varepsilon :{\mathbb {N}}\to {\mathbb {N}}$
satisfying
$M_\varepsilon :{\mathbb {N}}\to {\mathbb {N}}$
satisfying
 $\lim _{l\to \infty }({M_\varepsilon (l)}/l)=0$
, such that any finite specification (with any finite number
$\lim _{l\to \infty }({M_\varepsilon (l)}/l)=0$
, such that any finite specification (with any finite number
 $N_1$
of orbit segments) satisfying, for each
$N_1$
of orbit segments) satisfying, for each
 $N\in [1,N_1]$
, the inequality
$N\in [1,N_1]$
, the inequality
 $g_N\ge M_\varepsilon (l_{N+1})$
is
$g_N\ge M_\varepsilon (l_{N+1})$
is
 $\varepsilon $
-shadowed by an orbit.
$\varepsilon $
-shadowed by an orbit.
The last condition asserts, roughly speaking, that any appropriately spaced finite sequence of orbit segments (where each gap is adjusted to the length of the following segment, according to the function
![]() $M_\varepsilon $
) can be
$M_\varepsilon $
) can be
![]() $\varepsilon $
-shadowed by a single orbit.
$\varepsilon $
-shadowed by a single orbit.
3. Preparatory statements
The proof of Theorem 1.3 relies on three key lemmas. The first one is concerned with increasingly good shadowing of certain infinite specifications.
Lemma 3.1. Let
![]() $(X,T)$
be a topological dynamical system with the weak specification property with a family of functions
$(X,T)$
be a topological dynamical system with the weak specification property with a family of functions
![]() $\{M_\varepsilon :\varepsilon>0\}$
. Let
$\{M_\varepsilon :\varepsilon>0\}$
. Let
![]() $(\varepsilon _k)_{k\ge 0}$
be a summable sequence of positive numbers. Let
$(\varepsilon _k)_{k\ge 0}$
be a summable sequence of positive numbers. Let
![]() $D=\bigcup _{N=1}^\infty [a_N,b_N]$
and let
$D=\bigcup _{N=1}^\infty [a_N,b_N]$
and let
![]() ${\mathcal S}:D\to X$
be an infinite specification satisfying, for some increasing sequence
${\mathcal S}:D\to X$
be an infinite specification satisfying, for some increasing sequence
![]() $(N_k)_{k\ge 0}$
of non-negative integers starting with
$(N_k)_{k\ge 0}$
of non-negative integers starting with
![]() $N_0=0$
, the following condition: for each
$N_0=0$
, the following condition: for each
![]() $k\ge 1$
and all
$k\ge 1$
and all
![]() $N\in [N_{k-1}+1,N_k]$
we have
$N\in [N_{k-1}+1,N_k]$
we have
Then there exists a point
![]() $x_0$
such that
$x_0$
such that
Proof. Let
![]() ${\mathcal S}_1$
denote the specification
${\mathcal S}_1$
denote the specification
![]() ${\mathcal S}$
restricted to the initial
${\mathcal S}$
restricted to the initial
![]() $N_1$
orbit segments. This finite specification satisfies the inequality
$N_1$
orbit segments. This finite specification satisfies the inequality
![]() $g_N\ge M_{\varepsilon _1}(l_{N+1})$
, hence it can be
$g_N\ge M_{\varepsilon _1}(l_{N+1})$
, hence it can be
![]() $\varepsilon _1$
-shadowed by the orbit of some point
$\varepsilon _1$
-shadowed by the orbit of some point
![]() $x_1\in X$
.
$x_1\in X$
.
We continue by induction. Suppose that we have found a point
![]() $x_k\in X$
which satisfies
$x_k\in X$
which satisfies
 $$ \begin{align} \kern-11pt\text{for all }{i\in[1,k]},\ \text{for all }{N\in[N_{i-1}+1,N_i]},\ \text{for all } {n\in[a_N,b_N]},\quad d({\mathcal S}(n),T^nx_k)\le\sum_{j=i}^k\varepsilon_j. \end{align} $$
$$ \begin{align} \kern-11pt\text{for all }{i\in[1,k]},\ \text{for all }{N\in[N_{i-1}+1,N_i]},\ \text{for all } {n\in[a_N,b_N]},\quad d({\mathcal S}(n),T^nx_k)\le\sum_{j=i}^k\varepsilon_j. \end{align} $$
We define a new specification
![]() ${\mathcal S}_{k+1}$
on
${\mathcal S}_{k+1}$
on
 $$ \begin{align*} [0,b_{N_k}]\cup\bigcup_{N=N_k+1}^{N_{k+1}}[a_N,b_N] \end{align*} $$
$$ \begin{align*} [0,b_{N_k}]\cup\bigcup_{N=N_k+1}^{N_{k+1}}[a_N,b_N] \end{align*} $$
as follows. We let
![]() ${\mathcal S}_{k+1}[0,b_{N_k}]=x_k[0,b_{N_k}]$
, while for
${\mathcal S}_{k+1}[0,b_{N_k}]=x_k[0,b_{N_k}]$
, while for
![]() $N\in [N_k+1,N_{k+1}]$
we let
$N\in [N_k+1,N_{k+1}]$
we let
![]() ${\mathcal S}_{k+1}[a_N,b_N]={\mathcal S}[a_N,b_N]$
. It will be convenient not to change the enumeration of the orbit segments (except for the first one, which is new), and of the gaps (the first gap of
${\mathcal S}_{k+1}[a_N,b_N]={\mathcal S}[a_N,b_N]$
. It will be convenient not to change the enumeration of the orbit segments (except for the first one, which is new), and of the gaps (the first gap of
![]() ${\mathcal S}_{k+1}$
coincides with the
${\mathcal S}_{k+1}$
coincides with the
![]() $N_k$
th gap of
$N_k$
th gap of
![]() ${\mathcal S}$
). Then
${\mathcal S}$
). Then
![]() ${\mathcal S}_{k+1}$
satisfies
${\mathcal S}_{k+1}$
satisfies
![]() $g_N\ge M_{\varepsilon _k}(l_{N+1})$
for all
$g_N\ge M_{\varepsilon _k}(l_{N+1})$
for all
![]() $N\in [N_k,N_{k+1}-1]$
(that is, for all gaps of
$N\in [N_k,N_{k+1}-1]$
(that is, for all gaps of
![]() ${\mathcal S}_{k+1}$
), hence it can be
${\mathcal S}_{k+1}$
), hence it can be
![]() $\varepsilon _k$
-shadowed by the orbit of some point
$\varepsilon _k$
-shadowed by the orbit of some point
![]() $x_{k+1}\in X$
. It is clear that
$x_{k+1}\in X$
. It is clear that
![]() $x_{k+1}$
satisfies (3.3) with the parameter
$x_{k+1}$
satisfies (3.3) with the parameter
![]() $k+1$
in place of k. This concludes the induction. We let
$k+1$
in place of k. This concludes the induction. We let
![]() $x_0$
be any accumulation point of the sequence
$x_0$
be any accumulation point of the sequence
![]() $(x_k)_{k\ge 1}$
. As easily seen, this point satisfies, for all
$(x_k)_{k\ge 1}$
. As easily seen, this point satisfies, for all
![]() $n\in D$
, the inequality
$n\in D$
, the inequality
 $$ \begin{align*} d({\mathcal S}(n),T^n(x_0))\le\sum_{j=k_n+1}^\infty\varepsilon_j, \end{align*} $$
$$ \begin{align*} d({\mathcal S}(n),T^n(x_0))\le\sum_{j=k_n+1}^\infty\varepsilon_j, \end{align*} $$
where
![]() $k_n$
is the unique integer
$k_n$
is the unique integer
![]() $k\ge 0$
such that
$k\ge 0$
such that
![]() $n\in [a_N,b_N]$
with
$n\in [a_N,b_N]$
with
![]() $N\in [N_k+1,N_{k+1}]$
. Since the sums on the right-hand side are tails of a convergent series, these distances tend to zero, as claimed.
$N\in [N_k+1,N_{k+1}]$
. Since the sums on the right-hand side are tails of a convergent series, these distances tend to zero, as claimed.
Remark 3.2. It is easily seen that if the domain D of
![]() ${\mathcal S}$
in the above lemma has density one then the point
${\mathcal S}$
in the above lemma has density one then the point
![]() $x_0$
from that lemma quasi-generates the same invariant measures as
$x_0$
from that lemma quasi-generates the same invariant measures as
![]() ${\mathcal S}$
.
${\mathcal S}$
.
The second key lemma requires two rather standard propositions from convex analysis. Although they are well known to specialists, it is hard to find them in the exact formulation. Thus, we provide them with proofs.
Let
![]() $(\mathcal M,d)$
be a compact convex set in a locally convex metric space (the reader may think of
$(\mathcal M,d)$
be a compact convex set in a locally convex metric space (the reader may think of
![]() $(\mathcal M(X),d)$
, where d is some standard metric compatible with the weak* topology). The elements of
$(\mathcal M(X),d)$
, where d is some standard metric compatible with the weak* topology). The elements of
![]() $\mathcal M$
will be denoted by the letters
$\mathcal M$
will be denoted by the letters
![]() $\mu ,\nu $
.
$\mu ,\nu $
.
Proposition 3.3. Let
![]() $T:\mathcal M\to \mathcal M$
be a continuous affine transformation. Then the set
$T:\mathcal M\to \mathcal M$
be a continuous affine transformation. Then the set
![]() $\mathcal M_T\subset \mathcal M$
, consisting of T-invariant elements, is non-empty and for any
$\mathcal M_T\subset \mathcal M$
, consisting of T-invariant elements, is non-empty and for any
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $n_\varepsilon\hspace{-1pt} \ge\hspace{-1pt} 1$
such that, for any
$n_\varepsilon\hspace{-1pt} \ge\hspace{-1pt} 1$
such that, for any
![]() $\nu\hspace{-1pt} \in\hspace{-1pt} \mathcal M$
and any
$\nu\hspace{-1pt} \in\hspace{-1pt} \mathcal M$
and any
![]() $n\hspace{-1pt}\ge\hspace{-1pt} n_\varepsilon $
, we have
$n\hspace{-1pt}\ge\hspace{-1pt} n_\varepsilon $
, we have
![]() $d((1/n)\sum _{i=0}^{n-1}T^i(\nu ), \mathcal M_T)\hspace{-1pt}<\hspace{-1pt}\varepsilon $
.
$d((1/n)\sum _{i=0}^{n-1}T^i(\nu ), \mathcal M_T)\hspace{-1pt}<\hspace{-1pt}\varepsilon $
.
Proof. We can assume that
![]() $\mathsf {diam}(\mathcal M)=1$
. Denote
$\mathsf {diam}(\mathcal M)=1$
. Denote
![]() $A_n(\nu )=(1/n)\sum _{i=1}^{n-1}T^i(\nu )$
. Then, by convexity of the metric and diameter 1 of
$A_n(\nu )=(1/n)\sum _{i=1}^{n-1}T^i(\nu )$
. Then, by convexity of the metric and diameter 1 of
![]() $\mathcal M$
, we easily see that
$\mathcal M$
, we easily see that
This in turn implies that any limit point of any sequence of the form
![]() $A_n(\nu _n)$
(with
$A_n(\nu _n)$
(with
![]() $\nu _n\in \mathcal M$
) is T-invariant. Such limit points exist by compactness, hence we get that
$\nu _n\in \mathcal M$
) is T-invariant. Such limit points exist by compactness, hence we get that
![]() $\mathcal M_T\neq \emptyset $
. Suppose that the second part of the proposition does not hold. This means that there exist
$\mathcal M_T\neq \emptyset $
. Suppose that the second part of the proposition does not hold. This means that there exist
![]() $\varepsilon>0$
and an increasing sequence
$\varepsilon>0$
and an increasing sequence
![]() $(n_k)_{k\ge 1}$
of natural numbers, and a sequence
$(n_k)_{k\ge 1}$
of natural numbers, and a sequence
![]() $(\nu _k)_{k\ge 1}$
of points of
$(\nu _k)_{k\ge 1}$
of points of
![]() $\mathcal M$
, such that
$\mathcal M$
, such that
![]() $d(A_{n_k}(\nu _k),\mathcal M_T)\ge \varepsilon $
for all
$d(A_{n_k}(\nu _k),\mathcal M_T)\ge \varepsilon $
for all
![]() $k\ge 1$
. But we have just proved that all accumulation points of the sequence
$k\ge 1$
. But we have just proved that all accumulation points of the sequence
![]() $(A_{n_k}(\nu _k))_{k\ge 1}$
belong to
$(A_{n_k}(\nu _k))_{k\ge 1}$
belong to
![]() $\mathcal M_T$
, so we have a contradiction.
$\mathcal M_T$
, so we have a contradiction.
Recall that if
![]() $\xi $
is a probability measure on
$\xi $
is a probability measure on
![]() $\mathcal M$
then there exists a unique point
$\mathcal M$
then there exists a unique point
![]() $\mu \in \mathcal M$
, called the barycenter of
$\mu \in \mathcal M$
, called the barycenter of
![]() $\xi $
, such that for every affine continuous function f one has
$\xi $
, such that for every affine continuous function f one has
The barycenter map is denoted by either
![]() $\xi \mapsto \mathsf {bar}(\xi )$
or by
$\xi \mapsto \mathsf {bar}(\xi )$
or by
![]() $\xi \mapsto \int \nu \,d\xi (\nu )$
(the integral in the sense of Pettis). It is well known that if the set of all probability measures on
$\xi \mapsto \int \nu \,d\xi (\nu )$
(the integral in the sense of Pettis). It is well known that if the set of all probability measures on
![]() $\mathcal M$
is endowed with the weak* topology then the barycenter map
$\mathcal M$
is endowed with the weak* topology then the barycenter map
![]() $\xi \mapsto \mathsf {bar}(\xi )$
is continuous. In the next proposition, the reader may think of
$\xi \mapsto \mathsf {bar}(\xi )$
is continuous. In the next proposition, the reader may think of
![]() $\mathcal M$
representing
$\mathcal M$
representing
![]() $\mathcal M_T(X)$
in a dynamical system
$\mathcal M_T(X)$
in a dynamical system
![]() $(X,T)$
, and
$(X,T)$
, and
![]() $\mu $
representing an ergodic measure.
$\mu $
representing an ergodic measure.
Proposition 3.4. Let
![]() $\mu $
be an extreme point of
$\mu $
be an extreme point of
![]() $\mathcal M$
. Then for any
$\mathcal M$
. Then for any
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $\delta>0$
such that, whenever a probability measure
$\delta>0$
such that, whenever a probability measure
![]() $\xi $
on
$\xi $
on
![]() $\mathcal M$
satisfies
$\mathcal M$
satisfies
![]() $d(\mathsf {bar}(\xi ),\mu )<\delta $
, we have
$d(\mathsf {bar}(\xi ),\mu )<\delta $
, we have
Proof. If the statement is false then there exists a sequence of measures
![]() $(\xi _k)_{k\ge 1}$
on
$(\xi _k)_{k\ge 1}$
on
![]() $\mathcal M$
such that
$\mathcal M$
such that
![]() $\lim _{k\to \infty }\mathsf {bar}(\xi _k)=\mu $
and
$\lim _{k\to \infty }\mathsf {bar}(\xi _k)=\mu $
and
![]() $\xi _k\{\nu \in \mathcal M:d(\mu ,\nu )<\varepsilon \}\le 1-\varepsilon $
for each
$\xi _k\{\nu \in \mathcal M:d(\mu ,\nu )<\varepsilon \}\le 1-\varepsilon $
for each
![]() $k\ge 1$
. Since the function which associates to a measure
$k\ge 1$
. Since the function which associates to a measure
![]() $\xi $
the value
$\xi $
the value
![]() $\xi (U)$
, where U is an open set, is lower semicontinuous in the weak* topology, we get that if
$\xi (U)$
, where U is an open set, is lower semicontinuous in the weak* topology, we get that if
![]() $\xi $
is an accumulation point of the sequence
$\xi $
is an accumulation point of the sequence
![]() $(\xi _k)_{k\ge 1}$
then
$(\xi _k)_{k\ge 1}$
then
![]() $\xi \{\nu \in \mathcal M:d(\mu ,\nu )<\varepsilon \}\le 1-\varepsilon $
. On the other hand, by continuity of the barycenter map, we have
$\xi \{\nu \in \mathcal M:d(\mu ,\nu )<\varepsilon \}\le 1-\varepsilon $
. On the other hand, by continuity of the barycenter map, we have
![]() $\mathsf {bar}(\xi )=\mu $
. Since
$\mathsf {bar}(\xi )=\mu $
. Since
![]() $\mu $
is an extreme point of
$\mu $
is an extreme point of
![]() $\mathcal M$
, the only measure on
$\mathcal M$
, the only measure on
![]() $\mathcal M$
with barycenter at
$\mathcal M$
with barycenter at
![]() $\mu $
is the Dirac measure
$\mu $
is the Dirac measure
![]() $\delta _{\mu }$
. We conclude that
$\delta _{\mu }$
. We conclude that
![]() $\xi =\delta _{\mu }$
. This is a contradiction, since
$\xi =\delta _{\mu }$
. This is a contradiction, since
![]() $\delta _{\mu }\{\nu \in \mathcal M:d(\mu ,\nu )<\varepsilon \}=1$
.
$\delta _{\mu }\{\nu \in \mathcal M:d(\mu ,\nu )<\varepsilon \}=1$
.
We proceed with the second key lemma needed in the proof of Theorem 1.3.
Lemma 3.5. Let
![]() $\mu $
be an ergodic measure on a topological dynamical system
$\mu $
be an ergodic measure on a topological dynamical system
![]() $(X,T)$
which has the weak specification property. Let
$(X,T)$
which has the weak specification property. Let
![]() $x_0\in X$
be quasi-generic for
$x_0\in X$
be quasi-generic for
![]() $\mu $
and let
$\mu $
and let
![]() $\mathcal {J}=(n_k)_{k\ge 1}$
be a sequence along which
$\mathcal {J}=(n_k)_{k\ge 1}$
be a sequence along which
![]() $x_0$
generates
$x_0$
generates
![]() $\mu $
. Then there exist a point
$\mu $
. Then there exist a point
![]() $\bar x_0\in X$
generic for
$\bar x_0\in X$
generic for
![]() $\mu $
and a set
$\mu $
and a set
![]() $\mathbb M\subset {\mathbb {N}}$
of upper density one achieved along a subsequence of
$\mathbb M\subset {\mathbb {N}}$
of upper density one achieved along a subsequence of
![]() $\mathcal {J}$
, such that
$\mathcal {J}$
, such that
Proof. We start by fixing a summable sequence of positive numbers
![]() $(\varepsilon _k)_{k\ge 1}$
. In view of Lemma 3.1 and Remark 3.2, it suffices to construct a specification
$(\varepsilon _k)_{k\ge 1}$
. In view of Lemma 3.1 and Remark 3.2, it suffices to construct a specification
![]() ${\mathcal S}$
on a domain D satisfying the following four conditions:
${\mathcal S}$
on a domain D satisfying the following four conditions:
-
(1) the assumptions of Lemma 3.1;
-
(2) the domain D of
 ${\mathcal S}$
has density one;
${\mathcal S}$
has density one; -
(3)
 $\lim _{n\in \mathbb M} d({\mathcal S}(n),T^n(x_0))=0$
, where
$\lim _{n\in \mathbb M} d({\mathcal S}(n),T^n(x_0))=0$
, where
 $\mathbb M\subset D$
has upper density one achieved along a subsequence of
$\mathbb M\subset D$
has upper density one achieved along a subsequence of
 $\mathcal {J}$
;
$\mathcal {J}$
; -
(4)
 ${\mathcal S}$
is generic for
${\mathcal S}$
is generic for
 $\mu $
.
$\mu $
.
We choose a sequence of positive integers
![]() $(l_k)_{k\ge 0}$
. The sequence should grow so fast that the ratios
$(l_k)_{k\ge 0}$
. The sequence should grow so fast that the ratios
![]() ${M_{\varepsilon _k}(l_k)}/{l_k}$
are all smaller than one and tend to zero. For each
${M_{\varepsilon _k}(l_k)}/{l_k}$
are all smaller than one and tend to zero. For each
![]() $k\ge 1$
we let
$k\ge 1$
we let
![]() $L_k=l_k+M_{\varepsilon _k(l_k)}$
. Next, we replace
$L_k=l_k+M_{\varepsilon _k(l_k)}$
. Next, we replace
![]() $\mathcal J$
by a fast-growing subsequence and from now on
$\mathcal J$
by a fast-growing subsequence and from now on
![]() $\mathcal J=(n_k)_{k\ge 1}$
will denote that subsequence. Initially we require that the ratios
$\mathcal J=(n_k)_{k\ge 1}$
will denote that subsequence. Initially we require that the ratios
![]() ${l_k}/{n_k}$
and
${l_k}/{n_k}$
and
![]() ${n_k}/{n_{k+1}}$
tend to zero as k grows. More conditions on the speed of growth of the sequences
${n_k}/{n_{k+1}}$
tend to zero as k grows. More conditions on the speed of growth of the sequences
![]() $(l_k)_{k\ge 1}$
and
$(l_k)_{k\ge 1}$
and
![]() $(n_k)_{k\ge 1}$
will be specified later.
$(n_k)_{k\ge 1}$
will be specified later.
The specification
![]() ${\mathcal S}$
is created in three steps. The first auxiliary specification
${\mathcal S}$
is created in three steps. The first auxiliary specification
![]() ${\mathcal S}'$
is just a partition of the orbit of
${\mathcal S}'$
is just a partition of the orbit of
![]() $x_0$
without gaps. We begin by partitioning it into segments of length
$x_0$
without gaps. We begin by partitioning it into segments of length
![]() $L_1$
until we cover the coordinate
$L_1$
until we cover the coordinate
![]() $n_1$
. Then we continue by partitioning the remaining part of the orbit of
$n_1$
. Then we continue by partitioning the remaining part of the orbit of
![]() $x_0$
into segments of length
$x_0$
into segments of length
![]() $L_2$
until we cover the coordinate
$L_2$
until we cover the coordinate
![]() $n_2$
and so on. To be precise, we create segments
$n_2$
and so on. To be precise, we create segments
![]() ${\mathcal S}'[a_N,b_N]=x_0[a_N,b_N]$
(where
${\mathcal S}'[a_N,b_N]=x_0[a_N,b_N]$
(where
![]() $N\ge 1$
) satisfying:
$N\ge 1$
) satisfying:
-
(i)
 $a_1=0$
;
$a_1=0$
; -
(ii) for
 $N\ge 2$
,
$N\ge 2$
,
 $a_N=b_{N-1}+1$
;
$a_N=b_{N-1}+1$
; -
(iii)
 $b_N=a_N+L_k-1$
, for
$b_N=a_N+L_k-1$
, for
 $N\in [N_{k-1}+1,N_k]$
, where
$N\in [N_{k-1}+1,N_k]$
, where -
(iv) for each
 $k\ge 1$
,
$k\ge 1$
,
 $N_k$
is such that
$N_k$
is such that
 $n_k\in [a_{N_k},b_{N_k}]$
$n_k\in [a_{N_k},b_{N_k}]$
(for consistency of notation, we have let
![]() $N_0=0$
). It is elementary to see that, since the ratios
$N_0=0$
). It is elementary to see that, since the ratios
![]() ${M_{\varepsilon _k}(l_k)}/{l_k}$
and
${M_{\varepsilon _k}(l_k)}/{l_k}$
and
![]() ${l_k}/{n_k}$
tend to zero, the ratios
${l_k}/{n_k}$
tend to zero, the ratios
![]() ${b_{N_k}}/{n_k}$
tend to one. Thus, by Remark 2.1, the point
${b_{N_k}}/{n_k}$
tend to one. Thus, by Remark 2.1, the point
![]() $x_0$
generates
$x_0$
generates
![]() $\mu $
along the sequence
$\mu $
along the sequence
![]() $(b_{N_k})_{k\ge 1}$
. From now on, we redefine the sequence
$(b_{N_k})_{k\ge 1}$
. From now on, we redefine the sequence
![]() $\mathcal J$
to be
$\mathcal J$
to be
![]() $(b_{N_k})_{k\ge 1}$
(and let
$(b_{N_k})_{k\ge 1}$
(and let
![]() $n_k=b_{N_k}$
; we also let
$n_k=b_{N_k}$
; we also let
![]() $n_0=0$
). This new sequence still satisfies
$n_0=0$
). This new sequence still satisfies
![]() ${n_k}/{n_{k+1}}\to 0$
.
${n_k}/{n_{k+1}}\to 0$
.
The empirical measures
![]() $\mu _{x_0[0,n_k]}$
tend to
$\mu _{x_0[0,n_k]}$
tend to
![]() $\mu $
. Since
$\mu $
. Since
![]() $n_{k-1}$
is eventually negligible in comparison with
$n_{k-1}$
is eventually negligible in comparison with
![]() $n_k$
, the following statement holds:
$n_k$
, the following statement holds:
The second auxiliary specification
![]() ${\mathcal S}"$
is obtained from
${\mathcal S}"$
is obtained from
![]() ${\mathcal S}'$
by truncating all orbit segments (except the first) on the left, to allow for future shadowing. More precisely, we let
${\mathcal S}'$
by truncating all orbit segments (except the first) on the left, to allow for future shadowing. More precisely, we let
![]() $a^{\prime }_1=a_1=0$
and for any
$a^{\prime }_1=a_1=0$
and for any
![]() $k\ge 1$
and any
$k\ge 1$
and any
![]() $N\in [N_{k-1}+1,N_k]$
(except for
$N\in [N_{k-1}+1,N_k]$
(except for
![]() $N=1$
) we let
$N=1$
) we let
![]() $a^{\prime }_N=a_N+M_{\varepsilon _k}(l_k)$
(since
$a^{\prime }_N=a_N+M_{\varepsilon _k}(l_k)$
(since
![]() $M_{\varepsilon _k}(l_k)<l_k$
, we have
$M_{\varepsilon _k}(l_k)<l_k$
, we have
![]() $a_N'<b_N$
). Then on the new domain
$a_N'<b_N$
). Then on the new domain
we define the specification
![]() ${\mathcal S}"$
by
${\mathcal S}"$
by
![]() $S"[a^{\prime }_N,b_N]=x_0[a^{\prime }_N,b_N]$
. This new specification has, for
$S"[a^{\prime }_N,b_N]=x_0[a^{\prime }_N,b_N]$
. This new specification has, for
![]() $N\in [N_{k-1}+1,N_k]$
(except for
$N\in [N_{k-1}+1,N_k]$
(except for
![]() $N=1$
), orbit segments of length
$N=1$
), orbit segments of length
![]() $l_k$
preceded by gaps of size
$l_k$
preceded by gaps of size
![]() $M_{\varepsilon _k}(l_k)$
(the first orbit segment has length
$M_{\varepsilon _k}(l_k)$
(the first orbit segment has length
![]() $L_1$
and no preceding gap).
$L_1$
and no preceding gap).
It should be quite obvious that the lower density of D is achieved along the sequence
![]() $b_{N_k}+M_{\varepsilon _{k+1}(l_{k+1})}$
(this is the end of the first gap, larger than all preceding gaps). Because the ratios
$b_{N_k}+M_{\varepsilon _{k+1}(l_{k+1})}$
(this is the end of the first gap, larger than all preceding gaps). Because the ratios
![]() ${M_{\varepsilon _k}(l_k)}/{l_k}$
tend to zero, by choosing the numbers
${M_{\varepsilon _k}(l_k)}/{l_k}$
tend to zero, by choosing the numbers
![]() $n_k$
(and hence
$n_k$
(and hence
![]() $b_{N_k}$
) sufficiently large in comparison with
$b_{N_k}$
) sufficiently large in comparison with
![]() $M_{\varepsilon _{k+1}}(l_{k+1})$
, we can arrange that the density of D equals one, as required in (2).
$M_{\varepsilon _{k+1}}(l_{k+1})$
, we can arrange that the density of D equals one, as required in (2).
We now have to go back to the choice of the sequences
![]() $(l_k)$
and
$(l_k)$
and
![]() $(n_k)$
and impose more conditions on the speed of their growth. We select numbers
$(n_k)$
and impose more conditions on the speed of their growth. We select numbers
![]() $\delta _k\le \varepsilon _k$
according to Proposition 3.4 with respect to the numbers
$\delta _k\le \varepsilon _k$
according to Proposition 3.4 with respect to the numbers
![]() $\varepsilon _k$
and the ergodic measure
$\varepsilon _k$
and the ergodic measure
![]() $\mu $
in the role of the extreme point of the compact convex set
$\mu $
in the role of the extreme point of the compact convex set
![]() $\mathcal M_T(X)$
. If the numbers
$\mathcal M_T(X)$
. If the numbers
![]() $l_k$
are (a priori) chosen large enough, using Proposition 3.3, we can arrange that
$l_k$
are (a priori) chosen large enough, using Proposition 3.3, we can arrange that
-
• the empirical measures
 $\mu _{x_0[a^{\prime }_N,b_N]}$
with
$\mu _{x_0[a^{\prime }_N,b_N]}$
with
 $N\in [N_{k-1}+1,N_k]$
are
$N\in [N_{k-1}+1,N_k]$
are
 ${\delta _k}/3$
-close to some invariant measures henceforth denoted by
${\delta _k}/3$
-close to some invariant measures henceforth denoted by
 $\mu _N$
.
$\mu _N$
.
Also, by imposing fast enough growth of the numbers
![]() $n_k$
, we may achieve that:
$n_k$
, we may achieve that:
-
• the empirical measure
 $\mu _{x_0[n_{k-1}+1,n_k]}$
is
$\mu _{x_0[n_{k-1}+1,n_k]}$
is
 $({\delta _k}/3)$
-close to
$({\delta _k}/3)$
-close to
 $\mu $
(see (3.4));
$\mu $
(see (3.4)); -
• the empirical measures
 $\mu _{x_0[a_N,b_N]}$
with
$\mu _{x_0[a_N,b_N]}$
with
 $N\in [N_{k-1}+1,N_k]$
are
$N\in [N_{k-1}+1,N_k]$
are
 $({\delta _k}/3)$
-close to the respective empirical measures
$({\delta _k}/3)$
-close to the respective empirical measures
 $\mu _{x_0[a^{\prime }_N,b_N]}$
(and hence
$\mu _{x_0[a^{\prime }_N,b_N]}$
(and hence
 $\frac 23\delta _k$
-close to
$\frac 23\delta _k$
-close to
 $\mu _N$
).
$\mu _N$
).
Clearly, the empirical measure
![]() $\mu _{x_0[n_{k-1}+1,n_k]}=\mu _{x_0[a_{N_{k-1}+1},b_{N_k}]}$
equals the arithmetic average of the measures
$\mu _{x_0[n_{k-1}+1,n_k]}=\mu _{x_0[a_{N_{k-1}+1},b_{N_k}]}$
equals the arithmetic average of the measures
![]() $\mu _{x_0[a_N,b_N]}$
with
$\mu _{x_0[a_N,b_N]}$
with
![]() $N{\kern-1.2pt}\in{\kern-1.2pt} [N_{k-1}{\kern-1.2pt}+{\kern-1.2pt}1,N_k]$
. By convexity of the metric,
$N{\kern-1.2pt}\in{\kern-1.2pt} [N_{k-1}{\kern-1.2pt}+{\kern-1.2pt}1,N_k]$
. By convexity of the metric,
![]() $\mu $
is
$\mu $
is
![]() $\delta _k$
-close to the arithmetic average of the invariant measures
$\delta _k$
-close to the arithmetic average of the invariant measures
![]() $\mu _N$
with
$\mu _N$
with
![]() $N{\kern-1.2pt}\in{\kern-1.2pt} [N_{k-1}{\kern-1.2pt}+{\kern-1.2pt}1,N_k]$
. By Proposition 3.4, the vast majority of the invariant measures
$N{\kern-1.2pt}\in{\kern-1.2pt} [N_{k-1}{\kern-1.2pt}+{\kern-1.2pt}1,N_k]$
. By Proposition 3.4, the vast majority of the invariant measures
![]() $\mu _N$
are
$\mu _N$
are
![]() $\varepsilon _k$
-close to
$\varepsilon _k$
-close to
![]() $\mu $
, and hence the corresponding empirical measures
$\mu $
, and hence the corresponding empirical measures
![]() $\mu _{x_0[a^{\prime }_N,b_N]}$
are
$\mu _{x_0[a^{\prime }_N,b_N]}$
are
![]() $2\varepsilon _k$
-close to
$2\varepsilon _k$
-close to
![]() $\mu $
(we are using
$\mu $
(we are using
![]() $\delta _k<\varepsilon _k$
). More precisely, there are fewer than
$\delta _k<\varepsilon _k$
). More precisely, there are fewer than
![]() $\varepsilon _k(N_k-N_{k-1})$
parameters
$\varepsilon _k(N_k-N_{k-1})$
parameters
![]() $N\in [N_{k-1}+1,N_k]$
(we will call them ‘bad’), for which the measure
$N\in [N_{k-1}+1,N_k]$
(we will call them ‘bad’), for which the measure
![]() $\mu _{x_0[a^{\prime }_N,b_N]}$
is not
$\mu _{x_0[a^{\prime }_N,b_N]}$
is not
![]() $2\varepsilon _k$
-close to
$2\varepsilon _k$
-close to
![]() $\mu $
.
$\mu $
.
We can now perform the third step in creating the specification
![]() ${\mathcal S}$
. This is done by replacing in
${\mathcal S}$
. This is done by replacing in
![]() ${\mathcal S}"$
the segments
${\mathcal S}"$
the segments
![]() $x_0[a^{\prime }_N,b_N]$
corresponding to ‘bad’ parameters
$x_0[a^{\prime }_N,b_N]$
corresponding to ‘bad’ parameters
![]() $N\in [N_{k-1},N_k]$
by orbit segments (of the same length) whose associated measures are
$N\in [N_{k-1},N_k]$
by orbit segments (of the same length) whose associated measures are
![]() $2\varepsilon _k$
-close to
$2\varepsilon _k$
-close to
![]() $\mu $
. For example, we can choose one ‘good’ parameter N (there exists such an N) and use the corresponding segment
$\mu $
. For example, we can choose one ‘good’ parameter N (there exists such an N) and use the corresponding segment
![]() $x_0[a^{\prime }_N,b_N]$
everywhere we need to make a replacement. This concludes the construction of
$x_0[a^{\prime }_N,b_N]$
everywhere we need to make a replacement. This concludes the construction of
![]() ${\mathcal S}$
.
${\mathcal S}$
.
We need to verify that
![]() ${\mathcal S}$
satisfies the desired four properties.
${\mathcal S}$
satisfies the desired four properties.
(1) It is clear that the specification
![]() ${\mathcal S}$
was created in accordance with the assumptions of Lemma 3.1.
${\mathcal S}$
was created in accordance with the assumptions of Lemma 3.1.
(2) As we have already remarked, the domain D has density one.
(3) Note that
![]() ${\mathcal S}"$
agrees with the orbit of
${\mathcal S}"$
agrees with the orbit of
![]() $x_0$
on D (which has density one). Then
$x_0$
on D (which has density one). Then
![]() ${\mathcal S}$
differs from
${\mathcal S}$
differs from
![]() ${\mathcal S}"$
on a set whose frequency in the interval
${\mathcal S}"$
on a set whose frequency in the interval
![]() $[n_{k-1}+1,n_k]$
is at most
$[n_{k-1}+1,n_k]$
is at most
![]() $\varepsilon _k$
. Thus the set of the integers n for which
$\varepsilon _k$
. Thus the set of the integers n for which
![]() ${\mathcal S}(n)\neq {\mathcal S}"(n)$
(or
${\mathcal S}(n)\neq {\mathcal S}"(n)$
(or
![]() ${\mathcal S}(n)$
is not defined) has lower density zero achieved along the sequence
${\mathcal S}(n)$
is not defined) has lower density zero achieved along the sequence
![]() $\mathcal J$
. The complementary set
$\mathcal J$
. The complementary set
![]() $\mathbb M$
has upper density one achieved along
$\mathbb M$
has upper density one achieved along
![]() $\mathcal J$
, and on this set we have
$\mathcal J$
, and on this set we have
![]() ${\mathcal S}(n)=T^n(x_0)$
(which trivially implies the required condition
${\mathcal S}(n)=T^n(x_0)$
(which trivially implies the required condition
![]() $\lim _{n\in \mathbb M}\ d({\mathcal S}(n),T^nx_0)=0$
).
$\lim _{n\in \mathbb M}\ d({\mathcal S}(n),T^nx_0)=0$
).
(4) Consider a long initial segment of
![]() ${\mathcal S}$
(say,
${\mathcal S}$
(say,
![]() ${\mathcal S}|_{[1,n]\cap D}$
), and let k be such that
${\mathcal S}|_{[1,n]\cap D}$
), and let k be such that
![]() $N\in [N_{k-1}+1,N_k]$
, where N is determined by the inclusion
$N\in [N_{k-1}+1,N_k]$
, where N is determined by the inclusion
![]() $n\in [a_N,b_N]$
. Then
$n\in [a_N,b_N]$
. Then
![]() ${\mathcal S}|_{[1,n]\cap D}$
consists essentially of segments of two lengths:
${\mathcal S}|_{[1,n]\cap D}$
consists essentially of segments of two lengths:
![]() $l_{k-1}$
, whose associated empirical measures are
$l_{k-1}$
, whose associated empirical measures are
![]() $2\varepsilon _{k-1}$
-close to
$2\varepsilon _{k-1}$
-close to
![]() $\mu $
; and
$\mu $
; and
![]() $l_k$
, whose associated empirical measures are
$l_k$
, whose associated empirical measures are
![]() $2\varepsilon _k$
-close to
$2\varepsilon _k$
-close to
![]() $\mu $
(in either case we have
$\mu $
(in either case we have
![]() $2\varepsilon _{k-1}$
-closeness). This closeness need not apply to the initial part left of the coordinate
$2\varepsilon _{k-1}$
-closeness). This closeness need not apply to the initial part left of the coordinate
![]() $n_{k-1}$
, and to the terminal, perhaps incomplete, orbit segment whose length does not exceed
$n_{k-1}$
, and to the terminal, perhaps incomplete, orbit segment whose length does not exceed
![]() $L_k$
. Since both
$L_k$
. Since both
![]() $n_{k-1}$
and
$n_{k-1}$
and
![]() $L_k$
are negligible in comparison with
$L_k$
are negligible in comparison with
![]() $n_k$
(and hence with n), the two extreme pieces can be ignored and we get that the empirical measure associated with
$n_k$
(and hence with n), the two extreme pieces can be ignored and we get that the empirical measure associated with
![]() ${\mathcal S}|_{[1,n]\cap D}$
is (nearly)
${\mathcal S}|_{[1,n]\cap D}$
is (nearly)
![]() $2\varepsilon _{k-1}$
-close to
$2\varepsilon _{k-1}$
-close to
![]() $\mu $
. Since k tends to infinity as n grows,
$\mu $
. Since k tends to infinity as n grows,
![]() ${\mathcal S}$
is generic for
${\mathcal S}$
is generic for
![]() $\mu $
.
$\mu $
.
Lemma 3.6. Let
![]() $(X,T)$
be a topological dynamical system and let
$(X,T)$
be a topological dynamical system and let
![]() $\mu $
be an invariant measure on X. For each
$\mu $
be an invariant measure on X. For each
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $\delta>0$
which satisfies the following assertion.
$\delta>0$
which satisfies the following assertion.
Let
![]() $\mathcal P$
be a partition of X all of whose atoms have diameter not exceeding
$\mathcal P$
be a partition of X all of whose atoms have diameter not exceeding
![]() $\delta $
. Let
$\delta $
. Let
![]() ${\mathcal S}$
be a finite specification consisting of
${\mathcal S}$
be a finite specification consisting of
![]() $N_1$
orbit segments of length l separated by some gaps (
$N_1$
orbit segments of length l separated by some gaps (
![]() $N_1$
and l are arbitrary natural numbers, and the gaps are also arbitrary):
$N_1$
and l are arbitrary natural numbers, and the gaps are also arbitrary):
where
![]() $a_1\ge 0$
and, for each
$a_1\ge 0$
and, for each
![]() $N\in [1,N_1]$
, we have
$N\in [1,N_1]$
, we have
![]() $x_N\in X$
and
$x_N\in X$
and
![]() $a_{N+1}-a_N\ge l$
. Assume that for each
$a_{N+1}-a_N\ge l$
. Assume that for each
![]() $B\in \mathcal P^l=\bigvee _{n=0}^{l-1}T^{-n}(\mathcal P)$
the frequency relative to
$B\in \mathcal P^l=\bigvee _{n=0}^{l-1}T^{-n}(\mathcal P)$
the frequency relative to
![]() $(a_N)_{N\in [1,N_1]}$
,
$(a_N)_{N\in [1,N_1]}$
,
is
![]() $\delta /{|\mathcal P^l|}$
-close to
$\delta /{|\mathcal P^l|}$
-close to
![]() $\mu (B)$
(this imposes that
$\mu (B)$
(this imposes that
![]() $N_1$
must in fact be huge). Then the empirical measure associated with
$N_1$
must in fact be huge). Then the empirical measure associated with
![]() ${\mathcal S}$
,
${\mathcal S}$
,
 $$ \begin{align*} \mu_{\mathcal S}=\frac1{|D|}\sum_{n\in D}\delta_{{\mathcal S}(n)}, \end{align*} $$
$$ \begin{align*} \mu_{\mathcal S}=\frac1{|D|}\sum_{n\in D}\delta_{{\mathcal S}(n)}, \end{align*} $$
where
![]() $D=\bigcup _{N=1}^{N_1}[a_N,a_N+l-1]$
is the domain of
$D=\bigcup _{N=1}^{N_1}[a_N,a_N+l-1]$
is the domain of
![]() ${\mathcal S}$
, is
${\mathcal S}$
, is
![]() $\varepsilon $
-close to
$\varepsilon $
-close to
![]() $\mu $
.
$\mu $
.
Proof. Regardless of what metric d compatible with the weak* topology on
![]() $\mathcal M(X)$
we are using, there exist a finite family of continuous
$\mathcal M(X)$
we are using, there exist a finite family of continuous
![]() $[0,1]$
-valued functions (say,
$[0,1]$
-valued functions (say,
![]() $f_1,\ldots ,f_K$
) and a small positive number
$f_1,\ldots ,f_K$
) and a small positive number
![]() $\gamma $
such that if
$\gamma $
such that if
 $$ \begin{align*} \bigg|\!\int f_k\,d\mu_1 - \int f_k\,d\mu_2\bigg|<3\gamma \end{align*} $$
$$ \begin{align*} \bigg|\!\int f_k\,d\mu_1 - \int f_k\,d\mu_2\bigg|<3\gamma \end{align*} $$
for each
![]() $k\in [1,K]$
, then
$k\in [1,K]$
, then
![]() $d(\mu _1,\mu _2)<\varepsilon $
. Further, there exists
$d(\mu _1,\mu _2)<\varepsilon $
. Further, there exists
![]() $\beta $
such that each of the finitely functions
$\beta $
such that each of the finitely functions
![]() $f_k$
varies on each
$f_k$
varies on each
![]() $\beta $
-ball in X by less than
$\beta $
-ball in X by less than
![]() $\gamma $
. We let
$\gamma $
. We let
![]() $\delta =\min \{\beta ,\gamma \}$
. Let
$\delta =\min \{\beta ,\gamma \}$
. Let
![]() $\mathcal P$
be a partition of X as in the formulation of the lemma. Observe that if we replace each of the functions
$\mathcal P$
be a partition of X as in the formulation of the lemma. Observe that if we replace each of the functions
![]() $f_k$
by a function
$f_k$
by a function
![]() $\bar f_k$
constant on the atoms of
$\bar f_k$
constant on the atoms of
![]() $\mathcal P$
(say, assuming on each atom the supremum of
$\mathcal P$
(say, assuming on each atom the supremum of
![]() $f_k$
over that atom), then the integral of
$f_k$
over that atom), then the integral of
![]() $\bar f_k$
with respect to any probability measure differs from the integral of
$\bar f_k$
with respect to any probability measure differs from the integral of
![]() $f_k$
by at most
$f_k$
by at most
![]() $\gamma $
. So, in order to show that
$\gamma $
. So, in order to show that
![]() $d(\mu _{\mathcal S},\mu )<\varepsilon $
, it suffices to show that
$d(\mu _{\mathcal S},\mu )<\varepsilon $
, it suffices to show that
 $$ \begin{align*} \bigg|\!\int f\,d\mu_{\mathcal S} - \int f\,d\mu\bigg|<\gamma, \end{align*} $$
$$ \begin{align*} \bigg|\!\int f\,d\mu_{\mathcal S} - \int f\,d\mu\bigg|<\gamma, \end{align*} $$
for any
![]() $[0,1]$
-valued (not necessarily continuous) function f constant on the atoms of
$[0,1]$
-valued (not necessarily continuous) function f constant on the atoms of
![]() $\mathcal P$
. For such a function f we have
$\mathcal P$
. For such a function f we have
 $$ \begin{align*} \int f\,d\mu_{\mathcal S} = \frac1{|D|}\sum_{N=1}^{N_1} \sum_{n=0}^{l-1}f(T^nx_N)= \frac1{N_1}\sum_{N=1}^{N_1}\frac1l\sum_{n=0}^{l-1}f(T^nx_N) \end{align*} $$
$$ \begin{align*} \int f\,d\mu_{\mathcal S} = \frac1{|D|}\sum_{N=1}^{N_1} \sum_{n=0}^{l-1}f(T^nx_N)= \frac1{N_1}\sum_{N=1}^{N_1}\frac1l\sum_{n=0}^{l-1}f(T^nx_N) \end{align*} $$
(we are using the obvious fact that
![]() $|D|=N_1l$
). Note that if, for some
$|D|=N_1l$
). Note that if, for some
![]() $N,N'\in [1,N_1]$
, the points
$N,N'\in [1,N_1]$
, the points
![]() $x_N$
and
$x_N$
and
![]() $x_{N'}$
belong to the same atom B of
$x_{N'}$
belong to the same atom B of
![]() $\mathcal P^l$
then the averages
$\mathcal P^l$
then the averages
![]() $(1/l)\sum _{n=0}^{l-1}f(T^nx_N)$
and
$(1/l)\sum _{n=0}^{l-1}f(T^nx_N)$
and
![]() $(1/l)\sum _{n=0}^{l-1}f(T^nx_{N'})$
are equal, so, we can replace them by
$(1/l)\sum _{n=0}^{l-1}f(T^nx_{N'})$
are equal, so, we can replace them by
![]() $(1/l)\sum _{n=0}^{l-1}f(T^nx_B)$
, where
$(1/l)\sum _{n=0}^{l-1}f(T^nx_B)$
, where
![]() $x_B$
is a point in B not depending on N. Then our integral becomes
$x_B$
is a point in B not depending on N. Then our integral becomes
 $$ \begin{align*} \int f\,d\mu_{\mathcal S} = \sum_{B\in\mathcal P^l}\frac{|\{N\in[1,N_1]:x_N\in B\}|}{N_1}\frac1l\sum_{n=0}^{l-1}f(T^nx_B). \end{align*} $$
$$ \begin{align*} \int f\,d\mu_{\mathcal S} = \sum_{B\in\mathcal P^l}\frac{|\{N\in[1,N_1]:x_N\in B\}|}{N_1}\frac1l\sum_{n=0}^{l-1}f(T^nx_B). \end{align*} $$
By assumption, the coefficient
![]() ${|\{N\in [1,N_1]:x_N\in B\}|}/{N_1}$
equals
${|\{N\in [1,N_1]:x_N\in B\}|}/{N_1}$
equals
![]() $\mu (B)$
up to
$\mu (B)$
up to
![]() $\delta /{|\mathcal P^l|}$
, all the more so up to
$\delta /{|\mathcal P^l|}$
, all the more so up to
![]() $\gamma /{|\mathcal P^l|}$
. Since the averages
$\gamma /{|\mathcal P^l|}$
. Since the averages
![]() $(1/l)\sum _{n=0}^{l-1}f(T^nx_B)$
do not exceed one, we obtain that
$(1/l)\sum _{n=0}^{l-1}f(T^nx_B)$
do not exceed one, we obtain that
![]() $\int f\,d\mu _{\mathcal S}$
equals
$\int f\,d\mu _{\mathcal S}$
equals
 $$ \begin{align*} \sum_{B\in\mathcal P^l}\mu(B)\frac1l\sum_{n=0}^{l-1}f(T^nx_B) \end{align*} $$
$$ \begin{align*} \sum_{B\in\mathcal P^l}\mu(B)\frac1l\sum_{n=0}^{l-1}f(T^nx_B) \end{align*} $$
up to
![]() $\gamma $
. Finally, observe that the latter sum equals
$\gamma $
. Finally, observe that the latter sum equals
![]() $\int (1/l)\sum _{n=0}^{l-1}f\circ T^n\,d\mu $
, which, by invariance of
$\int (1/l)\sum _{n=0}^{l-1}f\circ T^n\,d\mu $
, which, by invariance of
![]() $\mu $
, equals
$\mu $
, equals
![]() $\int f\,d\mu $
. We have shown that
$\int f\,d\mu $
. We have shown that
![]() $|\int f\,d\mu _{\mathcal S} - \int f\,d\mu |<\gamma $
, as required.
$|\int f\,d\mu _{\mathcal S} - \int f\,d\mu |<\gamma $
, as required.
The next proposition is our last preparatory fact before the proof of Theorem 1.3 It is also a standard fact (this time from ergodic theory), whose exact formulation is hard to find. Thus, we provide it with a proof.
Proposition 3.7. Let
![]() $(X,T)$
be a topological dynamical system. Let x be a point quasi-generic for an ergodic measure
$(X,T)$
be a topological dynamical system. Let x be a point quasi-generic for an ergodic measure
![]() $\mu $
and let
$\mu $
and let
![]() $\mathcal J=(n_k)_{k\ge 1}$
be a sequence along which x generates
$\mathcal J=(n_k)_{k\ge 1}$
be a sequence along which x generates
![]() $\mu $
. Fix a positive integer L. Then there exist two increasing sequences of positive integers,
$\mu $
. Fix a positive integer L. Then there exist two increasing sequences of positive integers,
![]() $(a_N)_{N\ge 0}$
and
$(a_N)_{N\ge 0}$
and
![]() $(N_k)_{k\ge 1}$
, satisfying the following conditions.
$(N_k)_{k\ge 1}$
, satisfying the following conditions.
-
(1) For each
 $N\ge 1$
the difference
$N\ge 1$
the difference
 $a_{N+1}-a_N$
equals either L or
$a_{N+1}-a_N$
equals either L or
 $L+1$
.
$L+1$
. -
(2)
 $\lim _{k\to \infty }({a_{N_k}}/{n_k})=1$
(that is, the sequences
$\lim _{k\to \infty }({a_{N_k}}/{n_k})=1$
(that is, the sequences
 $(n_k)_{k\ge 1}$
and
$(n_k)_{k\ge 1}$
and
 $(a_{N_k})_{k\ge 1}$
are equivalent).
$(a_{N_k})_{k\ge 1}$
are equivalent). -
(3) x generates
 $\mu $
with respect to the sequence
$\mu $
with respect to the sequence
 $(a_N)_{N\ge 1}$
, along
$(a_N)_{N\ge 1}$
, along
 $(N_k)_{k\ge 1}$
, that is,
$(N_k)_{k\ge 1}$
, that is,  $$ \begin{align*} \lim_{k\ge1}\frac1{N_k}\sum_{N=1}^{N_k}\delta_{T^{a_N}(x)}=d\mu. \end{align*} $$
$$ \begin{align*} \lim_{k\ge1}\frac1{N_k}\sum_{N=1}^{N_k}\delta_{T^{a_N}(x)}=d\mu. \end{align*} $$
Proof. There exists an ergodic measure-preserving system
![]() $(Y,\nu ,S)$
disjoint from
$(Y,\nu ,S)$
disjoint from
![]() $(X,\mu ,T)$
(in the sense of Furstenberg). (Two measure-preserving systems are disjoint if their only joining is their product. An example of a system disjoint from
$(X,\mu ,T)$
(in the sense of Furstenberg). (Two measure-preserving systems are disjoint if their only joining is their product. An example of a system disjoint from
![]() $(X,\mu ,T)$
is an irrational rotation by
$(X,\mu ,T)$
is an irrational rotation by
![]() $e^{2\pi it}$
, where t is rationally independent from all numbers s such that
$e^{2\pi it}$
, where t is rationally independent from all numbers s such that
![]() $e^{2\pi is}$
is an eigenvalue of
$e^{2\pi is}$
is an eigenvalue of
![]() $(X,\mu ,T)$
(there are at most countably many values to be avoided).) By a standard application of Rokhlin towers, there exists a set A visited by
$(X,\mu ,T)$
(there are at most countably many values to be avoided).) By a standard application of Rokhlin towers, there exists a set A visited by
![]() $\nu $
-almost every orbit in Y infinitely many times with only two gap sizes between consecutive visits, L and
$\nu $
-almost every orbit in Y infinitely many times with only two gap sizes between consecutive visits, L and
![]() $L+1$
. There exists a topological model of
$L+1$
. There exists a topological model of
![]() $(Y,\nu ,S)$
in which the set A is clopen, that is, its indicator function, denoted by F, is continuous. Let
$(Y,\nu ,S)$
in which the set A is clopen, that is, its indicator function, denoted by F, is continuous. Let
![]() $y\in Y$
be a point generic for
$y\in Y$
be a point generic for
![]() $\nu $
and let
$\nu $
and let
![]() $(a_N)_{N\ge 1}$
denote the sequence of times of visits of the orbit of y in A (this sequence has only two gap sizes, L and
$(a_N)_{N\ge 1}$
denote the sequence of times of visits of the orbit of y in A (this sequence has only two gap sizes, L and
![]() $L+1$
, as required in (1)). The pair
$L+1$
, as required in (1)). The pair
![]() $(x,y)$
quasi-generates, along the sequence
$(x,y)$
quasi-generates, along the sequence
![]() $\mathcal J$
, some joinings of
$\mathcal J$
, some joinings of
![]() $\mu $
and
$\mu $
and
![]() $\nu $
. By disjointness, all such joinings are equal to the product measure
$\nu $
. By disjointness, all such joinings are equal to the product measure
![]() $\mu \times \nu $
on
$\mu \times \nu $
on
![]() $X\times Y$
, that is, along
$X\times Y$
, that is, along
![]() $\mathcal J$
the pair
$\mathcal J$
the pair
![]() $(x,y)$
generates
$(x,y)$
generates
![]() $\mu \times \nu $
. This implies that, for any continuous function f on X,
$\mu \times \nu $
. This implies that, for any continuous function f on X,
 $$ \begin{align*} \lim_{k\to\infty}\frac1{n_k}\sum_{n=1}^{n_k}f(T^nx)F(S^ny)&=\int f\,d\mu\cdot\nu(A),\\ \lim_{k\to\infty}\frac1{n_k}\sum_{n=1}^{n_k}F(S^ny)&=\nu(A). \end{align*} $$
$$ \begin{align*} \lim_{k\to\infty}\frac1{n_k}\sum_{n=1}^{n_k}f(T^nx)F(S^ny)&=\int f\,d\mu\cdot\nu(A),\\ \lim_{k\to\infty}\frac1{n_k}\sum_{n=1}^{n_k}F(S^ny)&=\nu(A). \end{align*} $$
Given
![]() $k\ge 1$
, let
$k\ge 1$
, let
![]() $N_k$
denote the largest N such that
$N_k$
denote the largest N such that
![]() $a_N\le n_k$
. Observe that since
$a_N\le n_k$
. Observe that since
![]() $(a_N)_{N\ge 1}$
has bounded gaps, while
$(a_N)_{N\ge 1}$
has bounded gaps, while
![]() $(n_k)_{k\ge 1}$
tends to infinity, the ratios
$(n_k)_{k\ge 1}$
tends to infinity, the ratios
![]() ${a_{N_k}}/{n_k}$
tend to one, as required in (2). Since
${a_{N_k}}/{n_k}$
tend to one, as required in (2). Since
![]() $F(S^ny)=1$
if and only if
$F(S^ny)=1$
if and only if
![]() $n=a_N$
for some N (otherwise
$n=a_N$
for some N (otherwise
![]() $F(S^ny)=0$
), we can rewrite the above limits as
$F(S^ny)=0$
), we can rewrite the above limits as
 $$ \begin{align} \lim_{k\to\infty}\frac1{n_k}\sum_{N=1}^{N_k}f(T^{a_N}x)&=\int f\,d\mu\cdot\nu(A), \end{align} $$
$$ \begin{align} \lim_{k\to\infty}\frac1{n_k}\sum_{N=1}^{N_k}f(T^{a_N}x)&=\int f\,d\mu\cdot\nu(A), \end{align} $$
Dividing the left/right hand side of (3.5) by the left/right hand side of (3.6), we get
 $$ \begin{align*} \lim_{k\to\infty}\frac1{N_k}\sum_{N=1}^{N_k}f(T^{a_N}x)=\int f\,d\mu. \end{align*} $$
$$ \begin{align*} \lim_{k\to\infty}\frac1{N_k}\sum_{N=1}^{N_k}f(T^{a_N}x)=\int f\,d\mu. \end{align*} $$
Since this is true for any continuous function f on X, we have proved (3).
4. The main proof
Proof of Theorem 1.3
Let
![]() $\mathcal J=(n_k)_{k\ge 1}$
be a sequence along which y generates
$\mathcal J=(n_k)_{k\ge 1}$
be a sequence along which y generates
![]() $\nu $
. It suffices to construct a point
$\nu $
. It suffices to construct a point
![]() $x_0$
such that the pair
$x_0$
such that the pair
![]() $(x_0,y)$
generates
$(x_0,y)$
generates
![]() $\xi $
along a subsequence
$\xi $
along a subsequence
![]() $\mathcal J'$
of
$\mathcal J'$
of
![]() $\mathcal {J}$
. Clearly, such an
$\mathcal {J}$
. Clearly, such an
![]() $x_0$
generates
$x_0$
generates
![]() $\mu $
along
$\mu $
along
![]() $\mathcal J'$
and, by Lemma 3.5, there will then exist a point x generic for
$\mathcal J'$
and, by Lemma 3.5, there will then exist a point x generic for
![]() $\mu $
and such that
$\mu $
and such that
where
![]() $\mathbb M$
is a set of upper density one achieved along a subsequence
$\mathbb M$
is a set of upper density one achieved along a subsequence
![]() $\mathcal J"$
of
$\mathcal J"$
of
![]() $\mathcal J'$
. Note that then the pair
$\mathcal J'$
. Note that then the pair
![]() $(x,y)$
still generates
$(x,y)$
still generates
![]() $\xi $
along
$\xi $
along
![]() $\mathcal J"$
, so the proof will be completed.
$\mathcal J"$
, so the proof will be completed.
We fix a summable sequence of positive numbers
![]() $(\varepsilon _k)_{k\ge 1}$
and an increasing sequence of natural numbers
$(\varepsilon _k)_{k\ge 1}$
and an increasing sequence of natural numbers
![]() $l_k$
such that
$l_k$
such that
Next, we let
![]() $(\mathcal P_k)_{k\ge 1}$
be a sequence of measurable partitions of X such that, for each
$(\mathcal P_k)_{k\ge 1}$
be a sequence of measurable partitions of X such that, for each
![]() $k\ge 1$
, the diameters of the atoms of
$k\ge 1$
, the diameters of the atoms of
![]() $\mathcal P_k$
do not exceed the number
$\mathcal P_k$
do not exceed the number
![]() $\delta _k$
obtained from Lemma 3.6 for the measure
$\delta _k$
obtained from Lemma 3.6 for the measure
![]() $\mu $
and
$\mu $
and
![]() $\varepsilon _k$
in the role of
$\varepsilon _k$
in the role of
![]() $\varepsilon $
.
$\varepsilon $
.
The atoms of the partitions
![]() $\mathcal P_k^l=\bigvee _{i=0}^{l-1}T^{-i}(\mathcal P_k)$
, where
$\mathcal P_k^l=\bigvee _{i=0}^{l-1}T^{-i}(\mathcal P_k)$
, where
![]() $k\ge 1$
and
$k\ge 1$
and
![]() $l\ge 1$
, will be called blocks of X, while the atoms
$l\ge 1$
, will be called blocks of X, while the atoms
![]() $\mathcal P_k^{l_k}$
will be called blocks of order k of X.
$\mathcal P_k^{l_k}$
will be called blocks of order k of X.
Likewise, we let
![]() $(\mathcal Q_k)_{k\ge 1}$
be a sequence of partitions of Y with diameters bounded by
$(\mathcal Q_k)_{k\ge 1}$
be a sequence of partitions of Y with diameters bounded by
![]() $\delta _k$
. We can easily arrange the partitions
$\delta _k$
. We can easily arrange the partitions
![]() $\mathcal Q_k$
so that the orbit of y avoids the boundaries of the atoms of
$\mathcal Q_k$
so that the orbit of y avoids the boundaries of the atoms of
![]() $\mathcal Q_k$
for each
$\mathcal Q_k$
for each
![]() $k\ge 1$
. (The partition
$k\ge 1$
. (The partition
![]() $\mathcal Q_k$
can be constructed as follows. First we choose a finite open cover by
$\mathcal Q_k$
can be constructed as follows. First we choose a finite open cover by
![]() $\delta _k$
-balls
$\delta _k$
-balls
![]() $B(c_i,\delta _k)$
centered at some points
$B(c_i,\delta _k)$
centered at some points
![]() $c_i\in Y$
,
$c_i\in Y$
,
![]() $i=1,2,\ldots ,N$
,
$i=1,2,\ldots ,N$
,
![]() $N\in {\mathbb {N}}$
. There exists
$N\in {\mathbb {N}}$
. There exists
![]() $\delta _k'<\delta _k$
such that for any
$\delta _k'<\delta _k$
such that for any
![]() $\delta \in [\delta _k',\delta _k]$
, the balls
$\delta \in [\delta _k',\delta _k]$
, the balls
![]() $B(c_i,\delta )$
still cover Y. Note that, for each i, the
$B(c_i,\delta )$
still cover Y. Note that, for each i, the
![]() $\delta $
-spheres
$\delta $
-spheres
![]() $S(c_i,\delta )$
are disjoint for different values of
$S(c_i,\delta )$
are disjoint for different values of
![]() $\delta $
. Since there are uncountably many values of
$\delta $
. Since there are uncountably many values of
![]() $\delta $
while the orbit of y is countable, there exists a
$\delta $
while the orbit of y is countable, there exists a
![]() $\delta \in [\delta _k',\delta _k]$
such that all the spheres
$\delta \in [\delta _k',\delta _k]$
such that all the spheres
![]() $S(c_i,\delta )$
,
$S(c_i,\delta )$
,
![]() $i=1,2,\ldots ,N$
, avoid the orbit of y. The partition
$i=1,2,\ldots ,N$
, avoid the orbit of y. The partition
![]() $\mathcal Q_k$
is obtained by ‘disjointification’ of the cover by the balls
$\mathcal Q_k$
is obtained by ‘disjointification’ of the cover by the balls
![]() $B(c_i,\delta )$
. Then the boundaries of the atoms of
$B(c_i,\delta )$
. Then the boundaries of the atoms of
![]() $\mathcal Q_k$
are contained in the union of the
$\mathcal Q_k$
are contained in the union of the
![]() $\delta $
-spheres
$\delta $
-spheres
![]() $S(c_i,\delta )$
, and hence the partition has the desired property.) The atoms of
$S(c_i,\delta )$
, and hence the partition has the desired property.) The atoms of
![]() $\mathcal Q_k^l=\bigvee _{i=0}^{l-1}S^{-i}(\mathcal Q_k)$
, where
$\mathcal Q_k^l=\bigvee _{i=0}^{l-1}S^{-i}(\mathcal Q_k)$
, where
![]() $k\ge 1$
and
$k\ge 1$
and
![]() $l\ge 1$
, will be called blocks of Y and the atoms of
$l\ge 1$
, will be called blocks of Y and the atoms of
![]() $\mathcal Q_k^{l_k}$
will be called atoms of order k of Y.
$\mathcal Q_k^{l_k}$
will be called atoms of order k of Y.
Note that if we apply the maximum metric in
![]() $X\times Y$
then the rectangular atoms of the partitions
$X\times Y$
then the rectangular atoms of the partitions
![]() $\mathcal P_k\otimes {\mathcal Q}_k$
have diameters bounded by
$\mathcal P_k\otimes {\mathcal Q}_k$
have diameters bounded by
![]() $\delta _k$
as well. We now choose some very small positive numbers
$\delta _k$
as well. We now choose some very small positive numbers
![]() $\gamma _k$
so that, for each
$\gamma _k$
so that, for each
![]() $k\ge 1$
, we have
$k\ge 1$
, we have
 $$ \begin{align*} 2\gamma_k+\gamma_k^2<\frac{\delta_k}{|\mathcal P_k^l\otimes\mathcal Q_k^l|}. \end{align*} $$
$$ \begin{align*} 2\gamma_k+\gamma_k^2<\frac{\delta_k}{|\mathcal P_k^l\otimes\mathcal Q_k^l|}. \end{align*} $$
Because y is generic for
![]() $\nu $
along
$\nu $
along
![]() $\mathcal J$
, and its orbit avoids the boundaries of the blocks, the orbit of y visits each block C of Y with frequency evaluated at times
$\mathcal J$
, and its orbit avoids the boundaries of the blocks, the orbit of y visits each block C of Y with frequency evaluated at times
![]() $n_k$
converging to
$n_k$
converging to
![]() $\nu (C)$
.
$\nu (C)$
.
Successively using Proposition 3.7 with the parameters
![]() $L_k=l_k+M_{\varepsilon _k}(l_k)$
in the role of L, and replacing, if necessary, the sequence
$L_k=l_k+M_{\varepsilon _k}(l_k)$
in the role of L, and replacing, if necessary, the sequence
![]() $\mathcal J$
by a rapidly growing subsequence
$\mathcal J$
by a rapidly growing subsequence
![]() $\mathcal J'$
(from now on
$\mathcal J'$
(from now on
![]() $(n_k)_{k\ge 1}$
will denote
$(n_k)_{k\ge 1}$
will denote
![]() $\mathcal J'$
), we can arrange two increasing sequences of positive integers,
$\mathcal J'$
), we can arrange two increasing sequences of positive integers,
![]() $(a_N)_{N\ge 1}$
and
$(a_N)_{N\ge 1}$
and
![]() $(N_k)_{k\ge 0}$
starting with
$(N_k)_{k\ge 0}$
starting with
![]() $N_0=0$
, satisfying the following conditions.
$N_0=0$
, satisfying the following conditions.
-
(1)
 ${\lim _{k\to \infty }({a_{N_k}}/{n_k})=1}$
.
${\lim _{k\to \infty }({a_{N_k}}/{n_k})=1}$
. -
(2) For each
 $k\ge 1$
and each
$k\ge 1$
and each
 $N\in [N_{k-1},N_k-1]$
, the difference
$N\in [N_{k-1},N_k-1]$
, the difference
 $a_{N+1}-a_N$
equals either
$a_{N+1}-a_N$
equals either
 $L_k$
or
$L_k$
or
 $L_k+1$
. (The proposition, as it is stated, does not allow us to ensure that the gap
$L_k+1$
. (The proposition, as it is stated, does not allow us to ensure that the gap
 $a_{N_k}-a_{N_k-1}$
(the first gap following the series of gaps of sizes
$a_{N_k}-a_{N_k-1}$
(the first gap following the series of gaps of sizes
 $L_k$
or
$L_k$
or
 $L_k+1$
) equals either
$L_k+1$
) equals either
 $L_{k+1}$
or
$L_{k+1}$
or
 $L_{k+1}+1$
. A priori, this gap may come out smaller (say, of size
$L_{k+1}+1$
. A priori, this gap may come out smaller (say, of size
 $j<L_{k+1}$
). However, in this case, replacing the set A in the proof of the proposition (for
$j<L_{k+1}$
). However, in this case, replacing the set A in the proof of the proposition (for
 $L=L_{k+1}$
) by
$L=L_{k+1}$
) by
 $T^{-(L_{k+1}-j)}A$
, we can adjust the gap to size
$T^{-(L_{k+1}-j)}A$
, we can adjust the gap to size
 $L_{k+1}$
.)
$L_{k+1}$
.) -
(3) If we denote by
 $C_N$
the unique block of order k of Y containing
$C_N$
the unique block of order k of Y containing
 $S^{a_N}y$
, then, for any block C of order k of Y, we have
$S^{a_N}y$
, then, for any block C of order k of Y, we have  $$ \begin{align*} \bigg|\frac1{N_k-N_{k-1}}|\{N\in[N_{k-1},N_k-1]:C_N=C\}|-\nu(C)\bigg|<\gamma_k. \end{align*} $$
$$ \begin{align*} \bigg|\frac1{N_k-N_{k-1}}|\{N\in[N_{k-1},N_k-1]:C_N=C\}|-\nu(C)\bigg|<\gamma_k. \end{align*} $$
-
(4) If, in addition, C satisfies
 $\nu (C)>0$
, then also
$\nu (C)>0$
, then also  $$ \begin{align*} |\{N\in[N_{k-1},N_k-1]:C_N=C\}|>\frac1{\gamma_k}. \end{align*} $$
$$ \begin{align*} |\{N\in[N_{k-1},N_k-1]:C_N=C\}|>\frac1{\gamma_k}. \end{align*} $$
Condition (1) says that
![]() $\mathcal J'$
and
$\mathcal J'$
and
![]() $\tilde {\mathcal J}'=(a_{N_k})_{k\ge 1}$
are equivalent. In particular, y generates
$\tilde {\mathcal J}'=(a_{N_k})_{k\ge 1}$
are equivalent. In particular, y generates
![]() $\nu $
along the sequence
$\nu $
along the sequence
![]() $(a_{N_k})_{k\ge 1}$
and if we find
$(a_{N_k})_{k\ge 1}$
and if we find
![]() $x_0$
using
$x_0$
using
![]() $\tilde {\mathcal J}'$
, the same
$\tilde {\mathcal J}'$
, the same
![]() $x_0$
will serve for
$x_0$
will serve for
![]() $\mathcal J'$
.
$\mathcal J'$
.
(*) Fix some
![]() $k\ge 1$
. Let
$k\ge 1$
. Let
![]() $\xi (B|C)={\xi (B\times C)}/{\nu (C)}$
, where B and C are blocks of order k of X and Y, respectively, with
$\xi (B|C)={\xi (B\times C)}/{\nu (C)}$
, where B and C are blocks of order k of X and Y, respectively, with
![]() $\nu (C)>0$
. For every such C, the numbers
$\nu (C)>0$
. For every such C, the numbers
![]() $\xi (B|C)$
, with B ranging over all blocks of order k of X, form a probability vector. By (4), this vector can be approximated up to
$\xi (B|C)$
, with B ranging over all blocks of order k of X, form a probability vector. By (4), this vector can be approximated up to
![]() $\gamma _k$
(at each coordinate) by a rational probability vector with entries
$\gamma _k$
(at each coordinate) by a rational probability vector with entries
where each
![]() $r(B,C)$
is a non-negative integer. We can thus create a finite sequence
$r(B,C)$
is a non-negative integer. We can thus create a finite sequence
![]() $(B_N)_{N\in [N_{k-1},N_k-1]}$
of blocks of order k of X, so that, for every pair of blocks
$(B_N)_{N\in [N_{k-1},N_k-1]}$
of blocks of order k of X, so that, for every pair of blocks
![]() $B,C$
of order k in X and Y respectively, we have
$B,C$
of order k in X and Y respectively, we have
Then, for each pair
![]() $B,C$
as above, with
$B,C$
as above, with
![]() $\nu (C)>0$
, we have
$\nu (C)>0$
, we have
where (by the choice of the integers
![]() $r(B,C)$
) the first fraction equals
$r(B,C)$
) the first fraction equals
![]() $\xi (B|C)$
up to
$\xi (B|C)$
up to
![]() $\gamma _k$
, and, by (3), the second fraction equals
$\gamma _k$
, and, by (3), the second fraction equals
![]() $\nu (C)$
, also up to
$\nu (C)$
, also up to
![]() $\gamma _k$
. So,
$\gamma _k$
. So,
![]() ${r(B,C)}/({N_k-N_{k-1}})$
equals
${r(B,C)}/({N_k-N_{k-1}})$
equals
![]() $\xi (B\times C)$
up to
$\xi (B\times C)$
up to
![]() $2\gamma _k+\gamma _k^2$
, which is less than
$2\gamma _k+\gamma _k^2$
, which is less than
![]() ${\delta _k}/{|\mathcal P_k^l\otimes \mathcal Q_k^l|}$
.
${\delta _k}/{|\mathcal P_k^l\otimes \mathcal Q_k^l|}$
.
Now, we create a finite specification
![]() $\bar {\mathcal S}_k$
in
$\bar {\mathcal S}_k$
in
![]() $X\times Y$
, as follows. For each
$X\times Y$
, as follows. For each
![]() $N\in [N_{k-1}, N_k-1]$
we choose a point
$N\in [N_{k-1}, N_k-1]$
we choose a point
![]() $x_N\in B_N$
and we let
$x_N\in B_N$
and we let
(the starting point of the Nth orbit segment falls in
![]() $(B_N,C_N)$
, and the second coordinate agrees, along the entire specification, with the orbit of y). Note that by (2), the gaps in the domain of
$(B_N,C_N)$
, and the second coordinate agrees, along the entire specification, with the orbit of y). Note that by (2), the gaps in the domain of
![]() $\bar {\mathcal S}_k$
have only two sizes, zero or one. Lemma 3.6 now guarantees that the empirical measure
$\bar {\mathcal S}_k$
have only two sizes, zero or one. Lemma 3.6 now guarantees that the empirical measure
![]() $\mu _{\bar {\mathcal S}_k}$
is
$\mu _{\bar {\mathcal S}_k}$
is
![]() $\varepsilon _k$
-close to
$\varepsilon _k$
-close to
![]() $\xi $
.
$\xi $
.
Let
![]() $\bar {\mathcal S}$
be the infinite specification in
$\bar {\mathcal S}$
be the infinite specification in
![]() $X\times Y$
defined as follows: for each
$X\times Y$
defined as follows: for each
![]() $k\ge 1$
and each
$k\ge 1$
and each
![]() $N\in [N_{k-1},N_k-1]$
we let
$N\in [N_{k-1},N_k-1]$
we let
It is fairly obvious that
![]() $\bar {\mathcal S}$
generates
$\bar {\mathcal S}$
generates
![]() $\xi $
along the sequence
$\xi $
along the sequence
![]() $\tilde {\mathcal J}'$
(by (4.1), the fact that the intervals of the domain are slightly trimmed on the left does not affect the convergence).
$\tilde {\mathcal J}'$
(by (4.1), the fact that the intervals of the domain are slightly trimmed on the left does not affect the convergence).
Let us denote by
![]() ${\mathcal S}$
the projection of
${\mathcal S}$
the projection of
![]() $\bar {\mathcal S}$
to the first coordinate. This infinite specification in X satisfies all requirements of Lemma 3.1. That lemma allows us to find a point
$\bar {\mathcal S}$
to the first coordinate. This infinite specification in X satisfies all requirements of Lemma 3.1. That lemma allows us to find a point
![]() $x_0$
whose orbit shadows the specification
$x_0$
whose orbit shadows the specification
![]() ${\mathcal S}$
with an increasing accuracy. Clearly, the pair
${\mathcal S}$
with an increasing accuracy. Clearly, the pair
![]() $(x_0,y)$
shadows
$(x_0,y)$
shadows
![]() $\bar {\mathcal S}$
equally well. It is also clear that the domain of
$\bar {\mathcal S}$
equally well. It is also clear that the domain of
![]() $\bar {\mathcal S}$
has density one, which (by Remark 3.2) implies that the pair
$\bar {\mathcal S}$
has density one, which (by Remark 3.2) implies that the pair
![]() $(x_0,y)$
generates
$(x_0,y)$
generates
![]() $\xi $
along
$\xi $
along
![]() $\tilde {\mathcal J}'$
, and hence also along
$\tilde {\mathcal J}'$
, and hence also along
![]() $\mathcal J'$
. We have achieved all that was necessary to complete the proof.
$\mathcal J'$
. We have achieved all that was necessary to complete the proof.
Remark 4.1. It is possible to modify the proof and avoid the use of Lemma 3.5 (see below). Although the main proof itself becomes slightly longer, one can skip that lemma and the two auxiliary propositions altogether. There are two reasons why we have decided to present the longer argument.
-
(1) Lemma 3.5 is a generalization of Kamae’s Theorem 1 in [Reference KamaeK] and has some independent value of its own. It may turn out useful in further studies of systems with weak specification.
-
(2) By following the framework of the original proof, we show that T. Kamae has insightfully laid ground for further generalizations.
Sketch of the modified proof.
Go to the paragraph marked by (*). Divide the blocks B (of order k of X) into two families:
![]() $\mathcal B$
, of those whose associated empirical measures are close to
$\mathcal B$
, of those whose associated empirical measures are close to
![]() $\mu $
, and the rest. By the mean ergodic theorem, for large enough k, the joint measure of the blocks in
$\mu $
, and the rest. By the mean ergodic theorem, for large enough k, the joint measure of the blocks in
![]() $\mathcal B$
is very close to one. Thus, by an insignificant renormalization, we can make the vector of conditional probabilities
$\mathcal B$
is very close to one. Thus, by an insignificant renormalization, we can make the vector of conditional probabilities
![]() $\xi (B|C)$
, with B ranging over
$\xi (B|C)$
, with B ranging over
![]() $\mathcal B$
(and C fixed) probabilistic. From here we proceed as it is described except that each time we refer to B we use only the blocks from
$\mathcal B$
(and C fixed) probabilistic. From here we proceed as it is described except that each time we refer to B we use only the blocks from
![]() $\mathcal B$
. The specification
$\mathcal B$
. The specification
![]() $\bar {\mathcal S}_k$
will then have its X-coordinate consisting exclusively of blocks
$\bar {\mathcal S}_k$
will then have its X-coordinate consisting exclusively of blocks
![]() $B\in \mathcal B$
. The specification
$B\in \mathcal B$
. The specification
![]() ${\mathcal S}$
(the X-projection of
${\mathcal S}$
(the X-projection of
![]() $\bar {\mathcal S}$
) will consist of blocks whose empirical measures are getting closer and closer to
$\bar {\mathcal S}$
) will consist of blocks whose empirical measures are getting closer and closer to
![]() $\mu $
. If the numbers
$\mu $
. If the numbers
![]() $a_{N_k}$
grow sufficiently fast in comparison to the lengths
$a_{N_k}$
grow sufficiently fast in comparison to the lengths
![]() $l_k$
then, by an identical argument to that in the proof of Lemma 3.5, the specification
$l_k$
then, by an identical argument to that in the proof of Lemma 3.5, the specification
![]() ${\mathcal S}$
will be generic for
${\mathcal S}$
will be generic for
![]() $\mu $
and so will be the point
$\mu $
and so will be the point
![]() $x_0$
shadowing
$x_0$
shadowing
![]() ${\mathcal S}$
. Lemma 3.5 becomes irrelevant.
${\mathcal S}$
. Lemma 3.5 becomes irrelevant.
Question 4.2. If y is generic for
![]() $\nu $
, can the pair
$\nu $
, can the pair
![]() $(x,y)$
be obtained generic for
$(x,y)$
be obtained generic for
![]() $\xi $
(as in the original theorem of Kamae)? Is a stronger specification property of X necessary for that?
$\xi $
(as in the original theorem of Kamae)? Is a stronger specification property of X necessary for that?
Added in proof. While checking the proofs of our paper we became aware of an old paper of T. Kamae [Reference KamaeK1] which contains results which partially overlap with ours. He introduces the vague separation property (v.s.p.) under which he proves a lifting theorem similar to ours. The relation between the v.s.p. and weak specification remains to be clarified.