Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T08:30:56.017Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit group invariants for non-free Cantor actions

Part of: Smooth dynamical systems: general theory Topological dynamics

Published online by Cambridge University Press:  09 March 2020

STEVEN HURDER Open the ORCID record for STEVEN HURDER [Opens in a new window]  and
OLGA LUKINA
STEVEN HURDER
Affiliation:
Department of Mathematics, University of Illinois at Chicago, 322 SEO (m/c 249), 851 S. Morgan Street, Chicago, IL 60607-7045, USA email hurder@uic.edu
OLGA LUKINA
Affiliation:
Faculty of Mathematics, University of Vienna, Oskar-Morgenstern-Platz 1, 1090Vienna, Austria email olga.lukina@univie.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

A Cantor action is a minimal equicontinuous action of a countably generated group 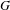$G$ on a Cantor space 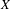$X$. Such actions are also called generalized odometers in the literature. In this work, we introduce two new conjugacy invariants for Cantor actions, the stabilizer limit group and the centralizer limit group. An action is wild if the stabilizer limit group is an increasing sequence of stabilizer groups without bound and otherwise is said to be stable if this group chain is bounded. For Cantor actions by a finitely generated group 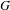$G$, we prove that stable actions satisfy a rigidity principle and furthermore show that the wild property is an invariant of the continuous orbit equivalence class of the action. A Cantor action is said to be dynamically wild if it is wild and the centralizer limit group is a proper subgroup of the stabilizer limit group. This property is also a conjugacy invariant and we show that a Cantor action with a non-Hausdorff element must be dynamically wild. We then give examples of wild Cantor actions with non-Hausdorff elements, using recursive methods from geometric group theory to define actions on the boundaries of trees.

Keywords

minimal Cantor actionscontinuous orbit equivalencerigiditynon-Hausdorff groupoids

MSC classification

Primary: 37B45: Continua theory in dynamics 37C15: Topological and differentiable equivalence, conjugacy, invariants, moduli, classification 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations
Secondary: 57S10: Compact groups of homeomorphisms
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 6 , June 2021 , pp. 1751 - 1794
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Álvarez López, J. and Candel, A.. Equicontinuous foliated spaces. Math. Z. 263 (2009), 725–774.CrossRefGoogle Scholar
Álvarez López, J. and Moreira Galicia, M.. Topological Molino’s theory. Pacific J. Math. 280 (2016), 257–314.Google Scholar
Auslander, J.. Minimal Flows and their Extensions (North-Holland Mathematics Studies, 153) . North-Holland, Amsterdam, 1988.Google Scholar
Bartholdi, L. and Nekrashevych, V.. Iterated monodromy groups of quadratic polynomials, I. Groups Geom. Dyn. 2 (2008), 309–336.CrossRefGoogle Scholar
Bezuglyi, S. and Medynets, K.. Full groups, flip conjugacy, and orbit equivalence of Cantor minimal systems. Colloq. Math. 110 (2008), 409–429.CrossRefGoogle Scholar
Boyle, M.. Topological orbit equivalence and factor maps in symbolic dynamics. PhD Thesis, University of Washington, 1983.Google Scholar
Boyle, M. and Tomiyama, J.. Bounded topological orbit equivalence and C ∗ -algebras. J. Math. Soc. Japan 50 (1998), 317–329.CrossRefGoogle Scholar
Brown, J., Clark, L., Orloff, L. and Farthing, C.. Simplicity of algebras associated to étale groupoids. Semigroup Forum 88 (2014), 433–452.CrossRefGoogle Scholar
Clark, A. and Hurder, S.. Homogeneous matchbox manifolds. Trans. Amer. Math. Soc. 365 (2013), 3151–3191.CrossRefGoogle Scholar
Clark, A., Hurder, S. and Lukina, O.. Classifying matchbox manifolds. Geom. Topol. 23 (2019), 1–38.CrossRefGoogle Scholar
Connes, A., Feldman, J. and Weiss, B.. An amenable equivalence relation is generated by a single transformation. Ergod. Th. & Dynam. Sys. 1 (1981), 431–450.CrossRefGoogle Scholar
Cortez, M. I. and Medynets, K.. Orbit equivalence rigidity of equicontinuous systems. J. Lond. Math. Soc. (2) 94 (2016), 545–556.CrossRefGoogle Scholar
Cortez, M.-I. and Petite, S.. G-odometers and their almost one-to-one extensions. J. Lond. Math. Soc. (2) 78 (2008), 1–20.CrossRefGoogle Scholar
Cortez, M. I. and Petite, S.. On the centralizers of minimal aperiodic actions on the Cantor set. Preprint, 2018, arXiv:1807.04654.Google Scholar
de Cornulier, Y.. Groupes pleins-topologiques (d’après Matui, Juschenko, Monod, …). Astérisque 361 (2014), 183–223.Google Scholar
Downarowicz, T.. Survey of odometers and Toeplitz flows. Algebraic and Topological Dynamics (Contemporary Mathematics, 385) . American Mathematical Society, Providence, RI, 2005, pp. 7–37.CrossRefGoogle Scholar
Dyer, J., Hurder, S. and Lukina, O.. The discriminant invariant of Cantor group actions. Topology Appl. 208 (2016), 64–92.CrossRefGoogle Scholar
Dyer, J., Hurder, S. and Lukina, O.. Growth and homogeneity of matchbox manifolds. Indag. Math. (N.S.) 28 (2017), 145–169.Google Scholar
Dyer, J., Hurder, S. and Lukina, O.. Molino theory for matchbox manifolds. Pacific J. Math. 289 (2017), 91–151.CrossRefGoogle Scholar
Eilenberg, S. and Steenrod, N.. Foundations of Algebraic Topology. Princeton University Press, Princeton, NJ, 1952.CrossRefGoogle Scholar
Ellis, R.. A semigroup associated with a transformation group. Trans. Amer. Math. Soc. 94 (1969), 272–281.Google Scholar
Ellis, R. and Gottschalk, W. H.. Homomorphisms of transformation groups. Trans. Amer. Math. Soc. 94 (1969), 258–271.CrossRefGoogle Scholar
Epstein, D. B. A., Millet, K. C. and Tischler, D.. Leaves without holonomy. J. Lond. Math. Soc. (2) 16 (1977), 548–552.CrossRefGoogle Scholar
Exel, R.. Non-Hausdorff étale groupoids. Proc. Amer. Math. Soc. 139 (2011), 897–907.Google Scholar
Fokkink, R. and Oversteegen, L.. Homogeneous weak solenoids. Trans. Amer. Math. Soc. 354(9) (2002), 3743–3755.CrossRefGoogle Scholar
Furman, A.. Orbit equivalence rigidity. Ann. of Math. (2) 150 (1999), 1083–1108.CrossRefGoogle Scholar
Gaboriau, D.. Orbit equivalence and measured group theory. Proc. Int. Congress Mathematicians, III. Hindustan Book Agency, New Delhi, 2010, pp. 1501–1527.Google Scholar
Giordano, T., Matui, H., Putnam, I. and Skau, C.. Orbit equivalence for Cantor minimal ℤ d -systems. Invent. Math. 179 (2010), 119–158.CrossRefGoogle Scholar
Giordano, T., Putman, I. and Skau, C.. Full groups of Cantor minimal systems. Israel J. Math. 111 (1999), 285–320.CrossRefGoogle Scholar
Giordano, T., Putman, I. and Skau, C.. ℤ d -odometers and cohomology. Groups Geom. Dyn. 13 (2019), 909–938.CrossRefGoogle Scholar
Glasner, E.. Enveloping semigroups in topological dynamics. Topology Appl. 154 (2007), 2344–2363.CrossRefGoogle Scholar
Glasner, E. and Weiss, B.. Weak orbit equivalence of Cantor minimal systems. Internat. J. Math. 6 (1995), 559–579.CrossRefGoogle Scholar
Grigorchuk, R. I.. Degrees of growth of finitely generated groups and the theory of invariant means. Izv. Akad. Nauk SSSR Ser. Mat. 48 (1984), 939–985.Google Scholar
Haefliger, A.. Pseudogroups of local isometries. Differential Geometry (Santiago de Compostela, 1984) (Research Notes in Mathematics, 131) . Ed. Cordero, L. A.. Pitman, Boston, MA, 1985, pp. 174–197.Google Scholar
Hurder, S. and Lukina, O.. Orbit equivalence and classification of weak solenoids. Indiana Univ. Math. J. to appear. Preprint, 2018, arXiv:1803.02098.Google Scholar
Hurder, S. and Lukina, O.. Wild solenoids. Trans. Amer. Math. Soc. 371 (2019), 4493–4533.CrossRefGoogle Scholar
Kobayashi, S. and Nomizu, K.. Foundations of Differential Geometry. Vol. II (Interscience Tracts in Pure and Applied Mathematics, 15) . Interscience–John Wiley, New York, 1969.Google Scholar
Li, X.. Continuous orbit equivalence rigidity. Ergod. Th. & Dynam. Sys. 38 (2018), 1543–1563.Google Scholar
Lukina, O.. Galois groups and Cantor actions. Submitted. Preprint, 2018, arXiv:1809.08475.Google Scholar
Lukina, O.. Arboreal Cantor actions. J. Lond. Math. Soc. (2) 99 (2019), 678–706.CrossRefGoogle Scholar
McCord, C.. Inverse limit sequences with covering maps. Trans. Amer. Math. Soc. 114 (1965), 197–209.CrossRefGoogle Scholar
Munkres, J.. Elements of Algebraic Topology. Addison-Wesley, Menlo Park, CA, 1984.Google Scholar
Nekrashevych, V.. Self-similar Groups (Mathematical Surveys and Monographs, 117) . American Mathematical Society, Providence, RI, 2005.CrossRefGoogle Scholar
Nekrashevych, V.. Palindromic subshifts and simple periodic groups of intermediate growth. Ann. of Math. (2) 187 (2018), 667–719.CrossRefGoogle Scholar
Pink, R.. Profinite iterated monodromy groups arising from quadratic polynomials. Preprint, 2013, arXiv:1307.5678.Google Scholar
Renault, J.. A Groupoid Approach to C ∗ -Algebras (Lecture Notes in Mathematics, 793) . Springer, Berlin, 1980.Google Scholar
Renault, J.. Transverse properties of dynamical systems. Representation Theory, Dynamical Systems, and Asymptotic Combinatorics (American Mathematical Society Translations Series 2, 217) . American Mathematical Society, Providence, RI, 2006, pp. 185–199.Google Scholar
Renault, J.. Cartan subalgebras in C ∗ -algebras. Irish Math. Soc. Bull. 61 (2008), 29–63.Google Scholar
Rogers, J. T. Jr. and Tollefson, J. L.. Homogeneous inverse limit spaces with non-regular covering maps as bonding maps. Proc. Amer. Math. Soc. 29 (1971), 417–420.CrossRefGoogle Scholar
Schori, R.. Inverse limits and homogeneity. Trans. Amer. Math. Soc. 124 (1966), 533–539.CrossRefGoogle Scholar
Winkelnkemper, E.. The graph of a foliation. Ann. Global Anal. Geom. 1 (1983), 51–75.CrossRefGoogle Scholar