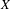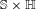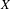Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Yonghong
and
Guo, Xunxiang
2019.
Sensitivities in Models with Backward Dynamics.
Discrete Dynamics in Nature and Society,
Vol. 2019,
Issue. ,
p.
1.
Díaz, Mauricio
2020.
12th Chaotic Modeling and Simulation International Conference.
p.
53.
Dhawan, Deepanshu
and
Sharma, Puneet
2024.
Various notions of shadowing in triangular system and its component systems.
Topology and its Applications,
Vol. 357,
Issue. ,
p.
109109.
Dhawan, Deepanshu
and
Sharma, Puneet
2025.
Notions of mixing and sensitivities for triangular map and its non-autonomous components.
Applied General Topology,
Vol. 26,
Issue. 2,
p.
601.
Pi, Jingmin
and
Yang, Qigui
2025.
Multivariate Li-Yorke sensitivity of non-autonomous discrete dynamical systems.
Journal of Mathematical Physics,
Vol. 66,
Issue. 10,
Pi, Jingmin
and
Yang, Qigui
2025.
Multivariate Li–Yorke chaos and multivariate distributional chaos in nonlinear dynamical systems.
Journal of Nonlinear Science,
Vol. 35,
Issue. 5,