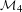${\mathcal{M}}_{4}$ is regular-closed

Abstract

For each 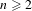$n\geq 2$, we investigate a family of iterated function systems which is parameterized by a common contraction ratio 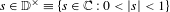$s\in \mathbb{D}^{\times }\equiv \{s\in \mathbb{C}:0<|s|<1\}$ and possesses a rotational symmetry of order $n$. Let 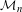${\mathcal{M}}_{n}$ be the locus of contraction ratio $s$ for which the corresponding self-similar set is connected. The purpose of this paper is to show that 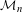${\mathcal{M}}_{n}$ is regular-closed, that is, 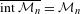$\overline{\text{int}\,{\mathcal{M}}_{n}}={\mathcal{M}}_{n}$ holds for 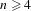$n\geq 4$. This gives a new result for 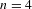$n=4$ and a simple geometric proof of the previously known result by Bandt and Hung [Fractal $n$-gons and their Mandelbrot sets. Nonlinearity 21 (2008), 2653–2670] for 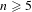$n\geq 5$.