Article contents
The maximal injective crossed product
Published online by Cambridge University Press: 22 April 2019
Abstract
A crossed product functor is said to be injective if it takes injective morphisms to injective morphisms. In this paper we show that every locally compact group 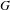 $G$ admits a maximal injective crossed product
$G$ admits a maximal injective crossed product 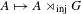 $A\mapsto A\rtimes _{\text{inj}}G$ . Moreover, we give an explicit construction of this functor that depends only on the maximal crossed product and the existence of
$A\mapsto A\rtimes _{\text{inj}}G$ . Moreover, we give an explicit construction of this functor that depends only on the maximal crossed product and the existence of 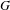 $G$ -injective
$G$ -injective 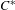 $C^{\ast }$ -algebras; this is a sort of ‘dual’ result to the construction of the minimal exact crossed product functor, the latter having been studied for its relationship to the Baum–Connes conjecture. It turns out that
$C^{\ast }$ -algebras; this is a sort of ‘dual’ result to the construction of the minimal exact crossed product functor, the latter having been studied for its relationship to the Baum–Connes conjecture. It turns out that 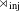 $\rtimes _{\text{inj}}$ has interesting connections to exactness, the local lifting property, amenable traces, and the weak expectation property.
$\rtimes _{\text{inj}}$ has interesting connections to exactness, the local lifting property, amenable traces, and the weak expectation property.
Keywords
MSC classification
Information
- Type
- Original Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2019
References
- 2
- Cited by


