Article contents
Measure preserving actions of affine semigroups and 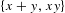 $\{x+y,xy\}$ patterns
$\{x+y,xy\}$ patterns
Published online by Cambridge University Press: 26 July 2016
Abstract
Ergodic and combinatorial results obtained in Bergelson and Moreira [Ergodic theorem involving additive and multiplicative groups of a field and 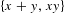 $\{x+y,xy\}$ patterns. Ergod. Th. & Dynam. Sys. to appear, published online 6 October 2015, doi:10.1017/etds.2015.68], involved measure preserving actions of the affine group of a countable field
$\{x+y,xy\}$ patterns. Ergod. Th. & Dynam. Sys. to appear, published online 6 October 2015, doi:10.1017/etds.2015.68], involved measure preserving actions of the affine group of a countable field 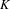 $K$ . In this paper, we develop a new approach, based on ultrafilter limits, which allows one to refine and extend the results obtained in Bergelson and Moreira, op. cit., to a more general situation involving measure preserving actions of the non-amenable affine semigroups of a large class of integral domains. (The results and methods in Bergelson and Moreira, op. cit., heavily depend on the amenability of the affine group of a field.) Among other things, we obtain, as a corollary of an ultrafilter ergodic theorem, the following result. Let
$K$ . In this paper, we develop a new approach, based on ultrafilter limits, which allows one to refine and extend the results obtained in Bergelson and Moreira, op. cit., to a more general situation involving measure preserving actions of the non-amenable affine semigroups of a large class of integral domains. (The results and methods in Bergelson and Moreira, op. cit., heavily depend on the amenability of the affine group of a field.) Among other things, we obtain, as a corollary of an ultrafilter ergodic theorem, the following result. Let 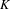 $K$ be a number field and let
$K$ be a number field and let 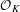 ${\mathcal{O}}_{K}$ be the ring of integers of
${\mathcal{O}}_{K}$ be the ring of integers of  $K$ . For any finite partition
$K$ . For any finite partition 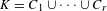 $K=C_{1}\cup \cdots \cup C_{r}$ , there exists
$K=C_{1}\cup \cdots \cup C_{r}$ , there exists 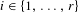 $i\in \{1,\ldots ,r\}$ such that, for many
$i\in \{1,\ldots ,r\}$ such that, for many 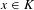 $x\in K$ and many
$x\in K$ and many 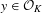 $y\in {\mathcal{O}}_{K}$ ,
$y\in {\mathcal{O}}_{K}$ , 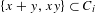 $\{x+y,xy\}\subset C_{i}$ .
$\{x+y,xy\}\subset C_{i}$ .
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2016
References
- 5
- Cited by

