Hostname: page-component-7f64f4797f-tldsr Total loading time: 0.001 Render date: 2025-11-04T00:36:39.468Z Has data issue: false hasContentIssue false
  • English
  • Français

Mutual information decay for factors of i.i.d.

Published online by Cambridge University Press:  29 April 2018

BALÁZS GERENCSÉR  and
VIKTOR HARANGI
BALÁZS GERENCSÉR
Affiliation:
MTA Alfréd Rényi Institute of Mathematics, H-1053 Budapest, Reáltanoda utca 13-15, Hungary email gerencser.balazs@renyi.mta.hu, harangi@renyi.hu ELTE Eötvös Loránd University, Department of Probability and Statistics, H-1117 Budapest, Pázmány Péter sétány 1/c, Hungary
VIKTOR HARANGI
Affiliation:
MTA Alfréd Rényi Institute of Mathematics, H-1053 Budapest, Reáltanoda utca 13-15, Hungary email gerencser.balazs@renyi.mta.hu, harangi@renyi.hu
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with factors of independent and identically distributed processes on the 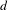$d$-regular tree for 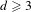$d\geq 3$. We study the mutual information of values on two given vertices. If the vertices are neighbors (i.e. their distance is $1$), then a known inequality between the entropy of a vertex and the entropy of an edge provides an upper bound for the (normalized) mutual information. In this paper we obtain upper bounds for vertices at an arbitrary distance 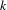$k$, of order 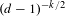$(d-1)^{-k/2}$. Although these bounds are sharp, we also show that an interesting phenomenon occurs here: for any fixed process, the rate of mutual information decay is much faster, essentially of order 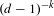$(d-1)^{-k}$.

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 11 , November 2019 , pp. 3015 - 3030
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Backhausz, Á., Gerencsér, B., Harangi, V. and Vizer, M.. Correlation bound for distant parts of factor of iid processes. Combin. Probab. Comput. 27(1) (2018), 1–20.Google Scholar
Backhausz, Á. and Szegedy, B.. On large girth regular graphs and random processes on trees. Preprint, 2014, arXiv:1406.4420.Google Scholar
Backhausz, Á. and Szegedy, B.. On the almost eigenvectors of random regular graphs. Preprint, 2016,arXiv:1607.04785.Google Scholar
Backhausz, Á., Szegedy, B. and Virág, B.. Ramanujan graphings and correlation decay in local algorithms. Random Struct. Alg. 47(3) (2015), 424–435.Google Scholar
Ball, K.. Factors of independent and identically distributed processes with non-amenable group actions. Ergod. Th. & Dynam. Sys. 25(3) (2005), 711–730.Google Scholar
Bollobás, B.. The independence ratio of regular graphs. Proc. Amer. Math. Soc. 83(2) (1981), 433–436.Google Scholar
Bowen, L.. A measure-conjugacy invariant for free group actions. Ann. Math. (2) 171(2) (2010), 1387–1400.Google Scholar
Bowen, L.. The ergodic theory of free group actions: entropy and the f-invariant. Groups Geom. Dyn. 4(3) (2010), 419–432.Google Scholar
Bowen, L.. Measure conjugacy invariants for actions of countable sofic groups. J. Amer. Math. Soc. 23(1) (2010), 217–245.Google Scholar
Csóka, E.. Independent sets and cuts in large-girth regular graphs. Preprint, 2016, arXiv:1602.02747.Google Scholar
Csóka, E., Gerencsér, B., Harangi, V. and Virág, B.. Invariant Gaussian processes and independent sets on regular graphs of large girth. Random Struct. Alg. 47(2) (2015), 284–303.Google Scholar
Harangi, V. and Virág, B.. Independence ratio and random eigenvectors in transitive graphs. Ann. Probab. 43(5) (2015), 2810–2840.Google Scholar
Hoppen, C. and Wormald, N.. Local algorithms, regular graphs of large girth, and random regular graphs. Combinatorica, to appear, arXiv:1308.0266.Google Scholar
Ornstein, D. S. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.10.1007/BF02790325Google Scholar
Rahman, M.. Factor of IID percolation on trees. SIAM J. Discrete Math. 30(4) (2016), 2217–2242.Google Scholar
Rahman, M. and Virág, B.. Local algorithms for independent sets are half-optimal. Ann. Probab. 45(3) (2017), 1543–1577.Google Scholar