New classes of quasigeodesic Anosov flows in $3$-manifolds

Abstract

Quasigeodesic behavior of flow lines is a very useful property in the study of Anosov flows. Not every Anosov flow in dimension three is quasigeodesic. In fact, until recently, up to orbit equivalence, the only previously known examples of quasigeodesic Anosov flows were suspension flows. In a recent article, the second author proved that an Anosov flow on a hyperbolic 3-manifold is quasigeodesic if and only if it is non-$\mathbb {R}$-covered, and this result completes the classification of quasigeodesic Anosov flows on hyperbolic 3-manifolds. In this article, we prove that a new class of examples of Anosov flows are quasigeodesic. These are the first examples of quasigeodesic Anosov flows on 3-manifolds that are neither Seifert, nor solvable, nor hyperbolic. In general, it is very hard to show that a given flow is quasigeodesic and, in this article, we provide a new method to prove that an Anosov flow is quasigeodesic.

1 Introduction

A flow on a manifold is called quasigeodesic if its orbits are uniformly efficient up to a bounded multiplicative and additive error in measuring distances when lifted to the universal cover. Quasigeodesics are extremely important for example in hyperbolic manifolds. This is because the Morse lemma says that on a hyperbolic space, any quasigeodesic is within a bounded distance from a length minimizing geodesic (when lifted to the universal cover) [Gro87, Thu82]. The distance depends on the quasigeodesic constants.

From the dynamical systems point of view, there are several important reasons to study hyperbolic flows, and in 3-manifolds, these are Anosov and pseudo-Anosov flows [Ano69, KH95, Mos92b]. The question as to whether an Anosov or a pseudo-Anosov flow in a closed hyperbolic 3-manifold is quasigeodesic has been intensively studied [Fen94, Fen95, Fen16, Fen22, FM01, Mos92a]. Now the quasigeodesic Anosov flows on hyperbolic 3-manifolds are fully classified by the second author [Fen94, Fen22]: an Anosov flow on a hyperbolic 3-manifold is quasigeodesic if and only if it is not $\mathbb {R}$ -covered. Here, $\mathbb {R}$ -covered means that the weak-stable leaf space (or equivalently, the weak-unstable leaf space) of the lifted flow in the universal cover is homeomorphic to $\mathbb {R}$ . In addition, it is known (and very easy to show) that any suspension flow is a quasigeodesic flow, in any manifold [Zeg93].

The question of quasigeodesic behavior for Anosov flows on non-hyperbolic 3-manifolds, which are not orbit equivalent to suspensions, has not been studied at all. The goal of this article is to start the study of the quasigeodesic property for Anosov flows in more general 3-manifolds.

First, we analyze Anosov flows in Seifert fibered 3-manifolds and prove the following.

Theorem 1.1. Let $\Phi $ be an Anosov flow in a closed, Seifert fibered $3$ -manifold. Then, $\Phi $ is a quasigeodesic flow.

To prove this theorem, we first show that, under an appropriate natural metric, flow lines of the geodesic flow on the unit tangent bundle of a hyperbolic surface are globally length minimizing (in the universal cover). An Anosov flow on a Seifert fibered manifold is orbitally equivalent to a finite lift of the geodesic flow on the unit tangent bundle of a hyperbolic surface. By using the orbit equivalence, we show that the flow lines of the Anosov flow on a Seifert fibered manifold are length minimizing up to finite bounds when lifted to the universal cover.

Notice that every Anosov flow on a solv manifold is also quasigeodesic. This is because Plante [Pl] proved that every Anosov flow in such a manifold is orbitally equivalent to a suspension Anosov flow.

We remark that not every Anosov flow is quasigeodesic: in [Fen94], the second author proved that there exist infinitely many examples of Anosov flows on three-dimensional hyperbolic manifolds which are not quasigeodesic. In addition, for a flow on a general manifold $\mathcal {M}$ , there might exist a Riemannian metric such that all the flow lines are geodesic (a differential geometric condition), but that does not guarantee that the flow lines are quasigeodesic.

The main result of this article proves the quasigeodesic property for Anosov flows in new classes of 3-manifolds. These manifolds have non-trivial JSJ decomposition [Hem76]. First, recall that the DA operation [Wil70] transforms a hyperbolic periodic orbit into either an attracting or repelling periodic orbit. Franks and Williams [FW80] used this operation to produce the first examples of non-transitive Anosov flows in dimension three as follows: they did a DA operation on a closed orbit of a suspension, producing a repelling orbit and an attractor. They removed a solid torus neighborhood of the periodic orbit to produce a flow in a manifold with boundary so that the flow is incoming along the boundary. They carefully glued this with a copy having a time-reversed flow. Under certain homotopy types of gluings, the resulting flow is Anosov. These examples revolutionized the study of Anosov flows in dimension three.

In modern terminology, the manifold with boundary, equipped with the incoming flow, is called a hyperbolic plug [BBY17]. In their article, Beguin, Bonatti, and Yu prove that under very general conditions, gluing hyperbolic plugs produces Anosov flows. In this article, we consider Anosov flows which we call generalized Franks–Williams flows. They are obtained as gluings of hyperbolic plugs as follows: start with a suspension Anosov flow and do a DA operation on finitely many periodic orbits. The operations are done so that either they all produce attracting orbits or they all produce repelling orbits. Then, remove a solid torus neighborhood from each DA orbit. Each plug contains either an attractor or a repeller. Glue finitely many of these plugs using the techniques of [BBY17]. The resulting flow is an Anosov flow [BBY17].

The main result of this article is the following.

Theorem 1.2. Let $\Phi $ be a generalized Franks–Williams Anosov flow in a closed $3$ -manifold M. Then, $\Phi $ is a uniform quasigeodesic flow.

Remark 1.3. This result is new in the sense that the manifolds in question are neither Seifert, nor hyperbolic, nor solvable. The JSJ decomposition is not trivial. It is easy to prove that the supporting manifolds of the hyperbolic plugs in question are atoroidal. In addition, by a result of Leeb [Lee95], a Haken manifold with at least one atoroidal piece in the JSJ decomposition can be given a Riemannian metric with non-positive sectional curvature, and hence the universal cover is $\mathrm {CAT}(0)$ with respect to the induced path metric. Therefore, the manifolds considered in Theorem 1.2 admit $\mathrm {CAT}(0)$ metrics.

1.1 Some ideas on the proof of Theorem 1.2

First, we mention a big difference from the case where the manifold is hyperbolic. As we remarked previously, much study has been done on the quasigeodesic property for Anosov flows in hyperbolic $3$ -manifolds. In these manifolds, a quasigeodesic satisfies that in the universal cover, it is at a bounded Hausdorff distance from a geodesic. On hyperbolic manifolds, geodesics are globally length minimizing curves in the universal cover. The bounded distance property is strongly connected with the quasigeodesic property, and in certain situations, it is an intermediate step in proving quasigeodesic behavior.

The manifolds in this article are not hyperbolic. In particular, a quasigeodesic in the universal cover may not be at a bounded Hausdorff distance from a minimal geodesic. This happens for example in Euclidean space. In the examples we study, there might exist quasi-flats in the universal cover—possible examples are lifts of the gluing tori and they behave like the Euclidean plane.

In this article, we analyze the flow in each individual block and then analyze how the blocks are assembled together. In each block, the flow is obtained from a blow up of a suspension Anosov flow, and hence it satisfies the quasigeodesic property when restricted to the block. The much more complicated property is to analyze orbits that cross the tori gluing different blocks. This turns out to be very intricate. We produced our flows so that we glue a collection of repellers to a collection of attractors. It follows that an orbit not contained in a plug intersects one (and only one) of the gluing tori, and goes from being near a repeller to being near an attractor. One potential problem is the following: it could happen that the segments of an orbit on either side of the gluing torus may track the torus for a long time and go in opposite directions. Lifting to the universal cover, one produces a big length along an orbit, but the distance between two points on the orbit may not be large enough compared with the length of orbit segment connecting them. In fact, if one considers arbitrary gluings on the gluing tori (and not just those generating Anosov flows as in [BBY17]), then this problem can occur and the flow is not quasigeodesic.

We do a very careful analysis to show that when the resulting flow is Anosov, then the flow lines are quasigeodesic. One crucial step is related to the potential problem above: we show that if a flow line intersects certain regions of a gluing tori, then the forward half-orbit ‘moves away efficiently’ from the lift of the torus when lifted to the universal cover. In other words, in the manifold, the forward orbit cannot keep tracking close to the torus for a long time. This result is Proposition 6.3 and it is the key component of the main result. Of course, this good behavior is not true for all orbits intersecting the torus and there is a bad region as well. To prove the quasigeodesic behavior, we have to consider both forward and backward half-orbits from points in the gluing tori, and how they are pierced together.

2 Preliminaries

A map $f:(X_1,d_1)\rightarrow (X_2,d_2)$ between two metric spaces $(X_1,d_1)$ and $(X_2,d_2)$ is a quasi-isometric embedding if there exist two constants $C>1$ and $c>0$ such that, for any points $p_1,p_2\in X_1$ ,

$$ \begin{align*}\frac{1}{C}d_1(p_1,p_2)-c\leq d_2(f(p_1),f(p_2))\leq Cd_1(p_1,p_2)+c.\end{align*} $$

A quasigeodesic in $(X_1,d_1)$ is a quasi-isometric embedding of an interval in $\mathbb {R}$ (with the standard metric) in $(X_1,d_1)$ ; the interval can be any of the forms $[a,b], [a,b), (a,b]$ , or $(a,b)\subset \mathbb {R}$ , where $a,b\in \mathbb {R}\cup \{+\infty , -\infty \}$ . If a or b is contained in the interval, then we assume it is not either of $+\infty , -\infty $ .

Suppose $\mathcal {N}$ is a closed Riemannian manifold with a Riemannian metric g and let the path metric induced by g be denoted by $d_{g}(\ ,\ )$ . A flow $\Phi _t$ on $\mathcal {N}$ with $C^1$ -orbits is called quasigeodesic if each flow line $\gamma $ of the lifted flow $\widetilde {\Phi }_t$ in the universal cover $\widetilde {\mathcal {N}}$ is a quasi-isometric embedding of $\mathbb {R}$ for some constants $C>1$ and $c>0$ . The metric in $\mathbb {R}$ is the path distance along the flow line. It is immediate that the quasigeodesic property of a flow line $\gamma $ in $\widetilde {\mathcal {N}}$ is equivalent to the following: there exists $C>1$ and $c>0$ such that for any two points $a,b\in \gamma $ ,

$$ \begin{align*}\text{length}_{\widetilde{g}}(\gamma_{[a,b]})\leq Cd_{\widetilde{g}}(a,b)+c,\end{align*} $$

where $\gamma _{[a,b]}$ is the flow segment connecting $a,b\in \gamma $ , $\widetilde {g}$ is the lift of the Riemannian metric g on $\widetilde {\mathcal {N}}$ , and $d_{\widetilde {g}}$ is the path metric on $\widetilde {\mathcal {N}}$ induced from $\widetilde {g}$ .

The definition is independent of the metric as the quasigeodesic property is preserved under quasi-isometric embeddings and, as our underlying manifold is compact, any two metrics in $\widetilde {\mathcal {N}}$ which are lifts from metrics in $\mathcal {N}$ are quasi-isometric to each other. However, the quasi-isometry constants may change.

If the same quasi-isometry constants $C>1$ and $c>0$ work for all the flow lines, then we say that the flow is uniformly quasigeodesic. It is not true that every quasigeodesic flow is uniform. Notice however that in closed hyperbolic manifolds, Calegari proved in [Cal06] that every quasigeodesic flow is uniformly quasigeodesic.

The focus of this article is to study the quasigeodesic behavior of Anosov flows in $3$ -manifolds. The $3$ -manifolds are always assumed to be closed.

Definition 2.1. A $C^1$ -flow $\Phi _t:\mathcal {M}\rightarrow \mathcal {M}$ on a Riemannian manifold $\mathcal {M}$ is Anosov if the tangent bundle $T\mathcal {M}$ splits into three $D\Phi _{t}$ -invariant sub-bundles $T\mathcal {M}=E^{s}\oplus E^{0} \oplus E^u$ and there exists two constants $B,b>0$ such that:

• • $E^0$ is generated by the non-zero vector field defined by the flow $\Phi _t$ ;

• • for any $v\in E^s$ and $t>0$ ,

  $$ \begin{align*}\|D\Phi_{t}(v)\|\leq Be^{-b t}\|v\|;\end{align*} $$

• • for any $w\in E^u$ and $t>0$ ,

  $$ \begin{align*}\|D\Phi_{t}(w)\|\geq Be^{b t}\|w\|.\end{align*} $$

The definition is independent of the choice of the Riemannian metric $\|.\|$ as the underlying manifold $\mathcal {M}$ is compact.

For a point $p\in \mathcal {M}$ , we will denote the flow line through p by $\gamma _p$ , that is, $\gamma _p=\{\Phi _t(p)|t\in \mathbb {R}\}$ . The collection of all flow lines of a flow defines a one-dimensional foliation on $\mathcal {M}$ . For an Anosov flow, there are several flow invariant foliations associated to the flow and these foliations play a key role in the study of Anosov flows.

Property 2.2. [Ano69]

For an Anosov flow $\Phi _t$ on $\mathcal {M}$ , the distributions $E^u$ , $E^s$ , $E^{0}\oplus E^{u}$ , and $E^{0}\oplus E^{s}$ are uniquely integrable. The associated foliations are denoted by $\mathcal {F}^u$ , $\mathcal {F}^s$ , $\mathcal {F}^{wu}$ , and $\mathcal {F}^{ws}$ , respectively, and they are called the strong unstable, strong stable, weak unstable, and weak stable foliation on $\mathcal {M}$ .

We conclude this section by introducing the notion of orbit equivalence between two flows $\Phi _t^1$ and $\Phi _t^2$ .

Definition 2.3. Two flows $\Phi _t^1:\mathcal {M}\rightarrow \mathcal {M}$ and $\Phi _t^2: \mathcal {N} \rightarrow \mathcal {N}$ are said to be orbit equivalent if there exists a homeomorphism $h:\mathcal {M}\rightarrow \mathcal {N}$ such that there exists a continuous map $\tau :\mathcal {N}\times \mathbb {R}\rightarrow \mathbb {R}$ such that $h\circ \Phi ^1_t\circ h^{-1}(x)=\Phi ^2_{\tau (x,t)}(x)$ for all $x\in \mathcal {N}$ . In addition, we require that $\tau $ preserves orientation in the $\mathbb {R}$ coordinate.

An orbit equivalence maps orbits to orbits with a possible time change. The requirement that h is a homeomorphism implies that $\tau $ restricted to $p \times \mathbb {R}$ is a homeomorphism for each p in M. The last condition means that this homeomorphism is orientation preserving for each p in M.

2.1 Organization of the article

In §3, we prove that geodesic flow on the unit tangent bundle of a hyperbolic surface is quasigeodesic. Moreover, Anosov flows on Seifert fibered 3-manifolds are quasigeodesic.

In §4, we describe the construction of generalized Franks–Williams flows and in §5, we describe the Riemannian metric we are going to work with in this article.

Section 6 contains the proof of Theorem 1.2; §6.1 proves the key proposition for the proof and §6.2 completes the proof.

3 Anosov flows in Seifert manifolds and quasigeodesic behavior

Suppose $\Sigma $ is a hyperbolic surface and $T\Sigma $ denotes its tangent bundle, that is, $T\Sigma =\{(p,v)|p\in \Sigma ,v\in T_p\Sigma \}$ . The universal cover of $\Sigma $ is the hyperbolic plane and we will consider the Poincaré upper-half-plane model $\mathbb {H}$ in this article, that is,

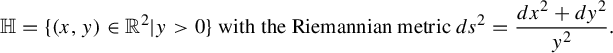$$ \begin{align*}\mathbb{H}=\{(x,y)\in\mathbb{R}^2|y>0\}\text{ with the Riemannian metric }ds^2=\frac{dx^2+dy^2}{y^2}.\end{align*} $$

On the tangent bundle $T\Sigma $ , we can define the geodesic vector field with respect to the metric $ds$ ; this is a classical construction, in this article, we follow the notation and the detailed description as in [doC92, Ch. 3].

Definition 3.1. The geodesic field is defined to be the unique vector field G on $T\Sigma $ whose trajectories are of the form $(\gamma (t),\gamma '(t))$ , where $\gamma $ is a geodesic on $\Sigma $ with respect to $ds$ .

The flow $\mathfrak {G}_t$ of the geodesic field is called the geodesic flow on $T\Sigma $ .

Suppose $\widetilde {\mathfrak {G}}_t$ is the lift of the geodesic flow on the universal cover $\widetilde {T\Sigma }=T\mathbb {H}=\mathbb {H}\times \mathbb {R}^2$ . We show that if $(\gamma (t),\gamma '(t))$ is a flow line of $\widetilde {\mathfrak {G}}_t$ on $T\mathbb {H}=\mathbb {H}\times \mathbb {R}^2$ , then it is a quasigeodesic in $T\mathbb {H}$ .

First, we choose an appropriate metric on $\widetilde {T\Sigma }$ which projects down to $T\Sigma $ . Consider the projection map $\pi :T\mathbb {H}\rightarrow \mathbb {H}$ . We can define a metric on $T\mathbb {H}$ using the projection $\pi $ and the metric $ds$ on $\mathbb {H}$ as described in [doC92, Ch. 3, Exercise 2], the following is the detailed description.

Suppose $(p,v)\kern1.4pt{\in}\kern1.4pt T\mathbb {H}$ , and consider $\alpha _1:t\kern1.4pt{\rightarrow}\kern1.4pt (p_1(t),v_1(t))$ and $\alpha _2:t\kern1.4pt{\rightarrow}\kern1.4pt (p_2(t),v_2(t))$ , where $p_1(0)=p_2(0)=p\in \mathbb {H}$ and $v_1(0)=v_2(0)=v\in T_p(\mathbb {H})$ . Let $V_1=\alpha _1'(0)$ and $V_2=\alpha _2'(0)$ . Then define the inner product as

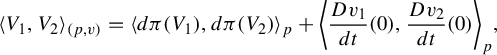$$ \begin{align*}\langle V_1,V_2\rangle_{(p,v)}=\langle d\pi(V_1),d\pi(V_2)\rangle_p+\bigg\langle\frac{Dv_1}{dt}(0),\frac{Dv_2}{dt}(0)\bigg\rangle_p,\end{align*} $$

where $\langle ,\rangle _p$ is given by the metric $ds$ on $\mathbb {H}$ and ${D}/{dt}$ denotes the covariant derivative as defined in [doC92, Proposition 2.2].

Clearly, the metric on $T\mathbb {H}$ as defined above projects down to $T\Sigma $ as the metric $ds$ on $\mathbb {H}$ projects down to $\Sigma $ . Abusing the notation, we denote metric on $T\Sigma $ by $ds$ .

Next, we prove that $\mathfrak {G}_t$ on $T\Sigma $ is a quasigeodesic flow. Suppose $(\gamma (t),\gamma '(t))$ is a flow line of $\widetilde {\mathfrak {G}}_t$ on $T\mathbb {H}$ , and let $(p,v)$ and $(q,w)$ be two points on $(\gamma ,\gamma ')$ . Consider a curve $\zeta :t\rightarrow (\zeta _1(t),\zeta _2(t))\in T\mathbb {H}$ on $t\in [0,1]$ such that $\zeta (0)=(p,v)$ and $\zeta (1)=(q,w)$ , and $\zeta _2(t)\in T_{\zeta _1(t)}\mathbb {H}$ for all $t\in [0,1]$ . Then,

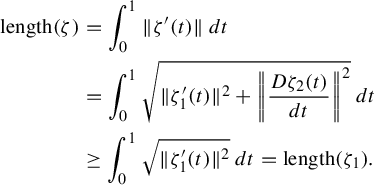(3.1) $$ \begin{align} \text{length}(\zeta)&=\int_0^1 \|\zeta'(t)\|\,dt\nonumber\\ &=\int^1_0\sqrt{\|\zeta_1'(t)\|^2+\bigg\|\frac{D\zeta_2(t)}{dt}\bigg\|^2}\,dt\nonumber\\ &\geq \int^1_0 \sqrt{\|\zeta_1'(t)\|^2}\,dt=\text{length}(\zeta_1). \end{align} $$

Note that $\zeta _1$ is a curve on $\mathbb {H}$ connecting $p,q\in \mathbb {H}$ . However, $\gamma $ is a geodesic on $\mathbb {H}$ and geodesics on $\mathbb {H}$ are globally length minimizing on $\mathbb {H}$ , which means

$$ \begin{align*}\text{length}(\zeta_1)\geq\text{length}(\gamma)\text{ between }p,q\in\mathbb{H}.\end{align*} $$

As $\gamma $ is a geodesic, the covariant derivative of $\gamma $ vanishes by definition, that is, ${D\gamma '}/{dt}=0$ . Using the fact that ${D\gamma '}/{dt}=0$ and the Riemannian metric on $T\mathbb {H}$ , it is easy to verify that

$$ \begin{align*}\text{length}(\gamma,\gamma')=\text{length}(\gamma)\text{ between }p,q\in\mathbb{H}.\end{align*} $$

Replacing in equation (3.1), we conclude that between $(p,v),(q,w)\in T\mathbb {H}$ ,

$$ \begin{align*}\text{length}(\zeta)\geq\text{length}(\zeta_1)\geq\text{length}(\gamma)=\text{length}(\gamma,\gamma').\end{align*} $$

As the choice of $(\gamma ,\gamma ')$ and $\zeta $ was arbitrary, the above inequality implies that the flow lines of $\widetilde {\mathfrak {G}}_t$ are globally length minimizing in $T\mathbb {H}$ , a stronger property than being a quasigeodesic. In other words, we proved the following.

Theorem 3.2. The flow lines of the geodesic flow $\widetilde {\mathfrak {G}}_t$ on $T\mathbb {H}$ are globally length minimizing. In particular, if $\Sigma $ is a hyperbolic surface, then the geodesic flow on $T\Sigma $ is a quasigeodesic flow.

3.1 Geodesic flows on the unit tangent bundle

We note that the flow lines of the geodesic flow on $T\Sigma $ are of the form $(\gamma ,\gamma ')$ . As $\gamma $ is a geodesic on $\Sigma $ , we get ${d}/{dt}\langle \gamma '(t),\gamma '(t)\rangle =0$ , that is, $\|\gamma '(t)\|=$ constant. This property allows us to restrict the flow $\mathfrak {G}_t$ on $T\Sigma $ to the unit tangent bundle $S\Sigma $ , where

$$ \begin{align*}S\Sigma=\{(p,v)|p\in\Sigma,v\in T_p\Sigma, \|v\|=1\}.\end{align*} $$

Similarly, we can restrict the flow $\widetilde {\mathfrak {G}}_t$ on $S\mathbb {H}$ , the unit tangent bundle on $\mathbb {H}$ . It is immediate by Theorem 3.2 that the flow lines of the geodesic flow on $S\mathbb {H}$ are globally length minimizing.

It is clear that $S\mathbb {H}$ is a cover of $S\Sigma $ , though it is not the universal cover. As the flow lines of the geodesic flow on $S\mathbb {H}$ are globally length minimizing and $S\mathbb {H}$ is complete, lifts of the flow lines of the geodesic flow in the universal cover $\widetilde {S\mathbb {H}}=\mathbb {H}\times \mathbb {R}$ are also globally length minimizing, a stronger property than being quasigeodesic.

So far, we have considered the metric $ds^2=({dx^2+dy^2})/{y^2}$ on $\mathbb {H}$ , and the geodesics and geodesic flow on a surface completely depend on the choice of Riemannian metric. However, geodesic flows associated with any two negatively curved metrics on a surface are orbit equivalent [Ghy84]. More precisely, there is a homeomorphism between the unit tangent bundles of the respective Riemannian metrics which takes orbits to orbits as described in Definition 2.3. It is easy to check that any homeomorphism between two compact manifolds gives a quasi-isometry when lifted to the universal covers. In particular, as unit tangent bundles of negatively curved closed surfaces are compact, the orbit equivalence maps are quasi-isometries between the universal covers; and quasi-isometries preserve quasigeodesics. This implies geodesic flow with respect to any negatively curved metric on a closed surface is quasigeodesic. We conclude the following theorem.

Theorem 3.3. If $\Sigma $ is a hyperbolic surface, the geodesic flows in the unit tangent bundle $S\Sigma $ is quasigeodesic. More precisely, the flow lines in the universal cover are globally length minimizing with respect to the metric $ds$ .

3.2 Anosov flows in Seifert manifolds

Now, we prove that any Anosov flow on a Seifert fibered 3-manifold is quasigeodesic. The following theorem relates Anosov flows on Seifert fibered 3-manifolds with geodesic flows.

Theorem 3.4. [Bar96]

Any Anosov flow on a closed Seifert fibered space is orbit equivalent to a finite lift of a geodesic flow on a hyperbolic surface.

We combine Theorems 3.3 and 3.4 to get the following.

Theorem 3.5. If $\Phi _t$ is an Anosov flow on a Seifert fibered 3-manifold $\mathcal {N}$ , then $\Phi _t$ is quasigeodesic.

Proof. By Theorem 3.4, $\Phi _t$ is orbit equivalent to a finite lift of the geodesic flow $\mathfrak {G}_t$ on the unit tangent bundle $S\Sigma $ of a hyperbolic surface $\Sigma $ . We denote the finite lift of $S\Sigma $ by $\widehat {S\Sigma }$ and the finite lift of the geodesic flow by $\widehat {\mathfrak {G}}_t$ .

Fix a Riemannian metric g on $\mathcal {N}$ . Let $\widehat {ds}$ be the metric on $\widehat {S\Sigma }$ , $\widehat {ds}$ which is the lift of the metric $ds$ as constructed before using the upper-half-plane $\mathbb {H}$ . This is the metric for which Theorem 3.4 holds. We denote the path metrics induced by the lifts of the metrics $\widetilde {g}$ and $\widetilde {ds}$ on $\widetilde {\mathcal {N}}$ and $\widetilde {S\Sigma }$ respectively by $d_1$ and $d_2$ .

Fix an orbit equivalence $h:\mathcal {N}\rightarrow \widehat {S\Sigma }$ and let $\widetilde {h}:\widetilde {\mathcal {N}}\rightarrow \widetilde {S\Sigma }$ be a lift of h to the universal covers. By the compactness of $\mathcal {N}$ and $\widehat {S\Sigma }$ , we can fix $\eta _1, \eta _2\text> 0$ such that for any $x,y\in \widetilde {\mathcal {N}}$ lying on the same flow line $\gamma $ ,

(3.2) $$ \begin{align} \text{if length}_{\widetilde{g}}(\gamma_{[x,y]})\geq \eta_1\quad\text{then length}_{\widetilde{ds}}(\widetilde{h}(\gamma_{[x,y]}))\geq\eta_2. \end{align} $$

Consider any two points $a_1,a_2\in \widetilde {\mathcal {N}}$ such that they are on the same flow line of $\gamma $ of $\widetilde {\Phi }_t$ . It is an easy exercise to prove the following using equation (3.2) and by Theorem 3.3:

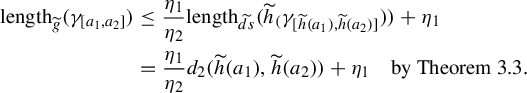(3.3) $$ \begin{align} \text{length}_{\widetilde{g}}(\gamma_{[a_1,a_2]}) &\leq \frac{\eta_1}{\eta_2} \text{length}_{\widetilde{ds}}(\widetilde{h}_(\gamma_{[\widetilde{h}(a_1),\widetilde{h}(a_2)]})) + \eta_1\nonumber\\ &= \frac{\eta_1}{\eta_2} d_2(\widetilde{h}(a_1),\widetilde{h}(a_2)) + \eta_1 \quad \text{by Theorem }3.3. \end{align} $$

Finally, as $h:\mathcal {N}\rightarrow \widehat {S\Sigma }$ is a homeomorphism between compact manifolds, the lifts to the universal covers induce quasi-isometries between the universal covers. Hence, there exists $\eta _3>1$ and $\eta _4> 0$ such that the map $\widetilde {h}^{-1}:(\widetilde {S\Sigma },d_{\widetilde {ds}})\rightarrow (\widetilde {\mathcal {N}},d_{\widetilde {g}})$ is an $(\eta _3,\eta _4)$ -quasi-isometry.

Applying the quasi-isometry $\widetilde {h}$ on (3.3), we get

$$ \begin{align*}\text{length}_{\widetilde{g}}(\gamma_{[a_1,a_2])})\ \leq \ \frac{\eta_1}{\eta_2}d_2(\widetilde{h}(a_1),\widetilde{h}(a_2)) + \eta_1\ \leq \ \frac{\eta_1}{\eta_2}(\eta_3 d_1(a_1,a_2)+\eta_4) + \eta_1.\end{align*} $$

Finally, let $A_0={\eta _1 \eta _3}/{\eta _2}$ and $A_1=({\eta _1 \eta _4}/{\eta _2}) + \eta _1$ . It follows that every flow line of $\widetilde {\Phi }_t$ is an $(A_0,A_1)$ -quasigeodesic.

4 Construction of generalized Franks–Williams flows

A common way to construct Anosov flows is to assemble building blocks. In general, a building block is a compact 3-manifold with boundary equipped with a non-singular vector field transverse to the boundary. In their article [BBY17], Bégui et al have combined many known ‘assembling building blocks’ techniques under a broad general criteria. The building blocks of these types of examples are called hyperbolic plugs (defined below). The first example of a non-transitive Anosov flow, that is, the Franks–Williams flow [FW80], is a classical example of this type of construction.

A plug is a pair $(\mathcal {M},V)$ , where $\mathcal {M}$ is a compact 3-manifold with boundary and V is a non-singular $C^1$ -vector field on $\mathcal {M}$ transverse to the boundary of $\mathcal {M}$ . The vector field induces a flow, denoted by $\mathcal {V}_t$ , on $\mathcal {M}$ . If $\mathcal {M}$ has non-empty boundary, the flow is not complete, that is, every orbit is defined on a closed time interval of $\mathbb {R}$ , but not every flow line is defined on the whole $\mathbb {R}$ . We consider the maximal invariant set $\Lambda $ of $\mathcal {V}_t$ , defined as $\Lambda :=\bigcap _{t\in \mathbb {R}}\mathcal {V}_t(\mathcal {M})$ . In other words, $\Lambda $ is the collection of all orbits which are defined for the whole $\mathbb {R}$ , equivalently these orbits do not intersect $\partial \mathcal {M}$ . If $\Lambda $ is a hyperbolic set, we say $(\mathcal {M},V)$ is a hyperbolic plug. Here is the precise definition.

Definition 4.1. A hyperbolic plug $(\mathcal {M},V)$ is a plug whose maximal invariant set $\Lambda $ is hyperbolic, which means, for every $x\in \Lambda $ , $T_x\mathcal {M}$ splits into three one-dimensional sub-bundles

$$ \begin{align*}T_x\mathcal{M}=E^s(x)\oplus\mathbb{R} V(x)\oplus E^u(x).\end{align*} $$

The bundle $E^s(x)$ (respectively $E^u(x)$ ) is called the stable (respectively unstable) bundle and there exists a Riemannian metric such that the differential of the time-one map of the flow uniformly contracts (respectively uniformly expands) the vectors of the stable bundle (respectively unstable bundle). The splitting varies continuously on $x\in \Lambda $ and is invariant under the derivative of the flow $\mathcal {V}_t$ .

The study of hyperbolic dynamics is an enormous area of study; here, we recall few of the preliminary properties (as in [BBY17]) required for this article, we refer to [KH95] for details:

• • for every $x\in \mathcal {M}$ , the strong stable manifold $W^{ss}(x)$ is defined as follows:

  $$ \begin{align*}W^{ss}(x)=\{y\in\mathcal{M}|\ d(\mathcal{V}_t(x),\mathcal{V}_t(y))\rightarrow 0\text{ as }t\rightarrow +\infty)\}.\end{align*} $$
  The strong unstable manifold is defined as the strong stable of the reversed flow $-\mathcal {V}_t$ ;

• • the weak stable manifold $W^{s}$ (respectively weak unstable manifold $W^u$ ) of a point ${x\in \mathcal {M}}$ is defined as the union of the strong stable manifolds (respectively strong unstable manifolds) of all points on the orbit of x;

• • there exists two 2-laminations, denoted by $W^s(\Lambda )$ and $W^u(\Lambda )$ , whose leaves are the weak stable and weak unstable manifolds, respectively, of the points of $\Lambda $ . The leaves of the laminations are $C^1$ -immersed manifolds tangent to continuous plane fields $E^s\oplus \mathbb {R} V(x)$ and $E^u\oplus \mathbb {R} V(x)$ .

The boundary of $\mathcal {M}$ is partitioned into two disjoint subsets, namely the exit boundary $\partial ^{\mathrm {out}}$ and the entrance boundary $ \partial ^{in}$ , where $\mathcal {V}_t$ points outwards on $\partial ^{\mathrm {out}}$ and inwards on $\partial ^{in}$ . If $\partial ^{\mathrm {out}}=\emptyset $ , then $(\mathcal {M},V)$ is an attracting plug and similarly $\partial ^{in}=\emptyset $ implies a repelling plug.

• • If both $\partial ^{in}\neq \emptyset $ and $\partial ^{\mathrm {out}}\neq \emptyset $ , then $\Lambda $ is a ‘saddle’. In that case, the weak stable lamination $W^{s}(\Lambda )$ intersects $\partial ^{in}$ transversally and forms a one-dimensional lamination $\mathcal {L}^{s}_{V}=\partial ^{in}\cap W^{s}$ on $\partial ^{in}$ . Similarly, the weak unstable lamination $W^{wu}(\Lambda )$ intersects $\partial ^{\mathrm {out}}$ in a one-dimensional lamination $\mathcal {L}^{u}_{V}=\partial ^{\mathrm {out}}\cap W^{u}$ .

• • For an attracting plug, $\Lambda $ is an attractor. In this case, the weak-stable lamination $W^{s}(\Lambda )$ intersects $\partial ^{in}$ in a one-dimensional lamination $\mathcal {L}^{s}_{V}=\partial ^{in}\cap W^{s}$ .

• • For a repelling plug, $\Lambda $ is a repeller. In this case, the weak-unstable lamination $W^{u}(\Lambda )$ intersects $\partial ^{\mathrm {out}}$ in a one-dimensional lamination $\mathcal {L}^{u}_{V}=\partial ^{\mathrm {out}}\cap W^{u}$ .

Proposition 4.2. [BBY17]

Consider a finite collection of hyperbolic plugs, denoted by $(\mathcal {M}_1, V_1), (\mathcal {M}_2, V_2),\ldots , (\mathcal {M}_n,V_n)$ . Assume that each of these plugs is either an attracting or a repelling plug. Let $\mathcal {D}^{\mathrm {out}}=\sqcup _{1}^{n}\partial ^{\mathrm {out}}(\mathcal {M}_i)$ and $\mathcal {D}^{in}=\sqcup _{1}^{n}\partial ^{in}(\mathcal {M}_i)$ . Suppose that the laminations $\mathcal {L}^s_{\mathcal {M}_i}, \mathcal {L}^u_{\mathcal {M}_j}$ (if they are non-empty) are filling laminations in the respective boundary components. Suppose there exists a diffeomorphism $\Omega :\mathcal {D}^{\mathrm {out}}\rightarrow \mathcal {D}^{in}$ such that $\Phi _*(\mathcal {L}^{s}_{\mathcal {M}_i})$ is transversal to $\mathcal {L}^{u}_{\mathcal {M}_j}$ on each appropriate component. Then the quotient vector field ${V_1\sqcup V_2\sqcup \cdots \sqcup V_n}/{\Omega }$ is Anosov on the quotient manifold ${\mathcal {M}_1\sqcup \mathcal {M}_2\sqcup \cdots \sqcup \mathcal {M}_n}/{\Omega }$ .

Since the plugs are either attractors or repellers, the laminations in the boundary are actually foliations and the glued Anosov flow is non-transitive. The result above is then [BBY17, Proposition 1.1].

In this article, we consider a special type of attracting and repelling plug, which we call a Franks–Williams-type hyperbolic plug. This type of of construction was first introduced by Franks and Williams in [FW80]. We construct our plugs using DA bifurcations of hyperbolic automorphisms on a 2-torus $\mathbb {T}^2$ . Details of the construction are described below.

4.1 Construction of the Franks–Williams-type hyperbolic plugs

Consider a hyperbolic linear automorphism A on the 2-torus $\mathbb {T}^2$ , which is induced by a linear map ${\widetilde {A}:\mathbb {R}^2\rightarrow \mathbb {R}}$ such that $\widetilde {A}$ has two eigenvalues $\lambda>1$ and $({1}/{\lambda })<1$ . On $\mathbb {T}^2$ , we have a pair of one-dimensional foliations, namely the stable $\mathcal {L}^s$ and unstable $\mathcal {L}^u$ foliations of the hyperbolic map A as described below.

• • Unstable foliation $\mathcal {L}^u: \mathbb {R}^2$ has a foliation $\tilde {\mathcal {L}}^u$ by the slope- $\lambda $ lines and this foliation is $\widetilde {A}$ -invariant. Hence, $\tilde {\mathcal {L}}^u$ on $\mathbb {R}^2$ projects down to a foliation on $\mathbb {T}^2$ and it is the unstable foliation $\mathcal {L}^u$ of A on $\mathbb {T}^2$ .

• • Stable foliation $\mathcal {L}^s$ : similarly, the foliation on $\mathbb {R}^2$ induced by the slope- ${1}/{\lambda }$ lines projects down to the stable foliation $\mathcal {L}^s$ of A on $\mathbb {T}^2$ .

These two foliations are everywhere transversal to each other on $\mathbb {T}^2$ . Hence, they define a two-frame $\{\mathscr {X},\mathscr {Y}\}$ on the tangent bundle $T\mathbb {T}^2$ , where $\mathscr {X}(p)$ is a vector in $T_p\mathbb {T}^2$ tangent to the stable direction and similarly, $\mathscr {Y}(p)$ is a vector tangent to the unstable direction in $T_p\mathbb {T}^2$ . In fact, we can define a new coordinate system $\{x,y\}$ on $\mathbb {R}^2$ .

A new coordinate system $\{x,y\}$ : fix a basis $\{v_{1/\lambda },v_{\lambda }\}$ on $\mathbb {R}^2$ , where the basis vectors are eigenvectors of the two distinct eigenvalues $\lambda $ and $1/\lambda $ . Then, the new coordinate system on $\mathbb {R}^2$ with respect to $\{v_{1/\lambda },v_{\lambda }\}$ is denoted by $\{x,y\}$ . In this coordinate, $\widetilde {A}$ can be written as $\widetilde {A}(x,y)=(({1}/{\lambda }) x,\lambda y)$ . We use this coordinate system extensively in the rest of the article.

The fixed point $(0,0)$ of $\widetilde {A}$ on $\mathbb {R}^2$ projects to a fixed point of A, denoted by $\mathfrak {o}$ , on $\mathbb {T}^2$ . We can change it to a point source or a point sink using the ‘Derived from Anosov(DA)’ bifurcation on a neighborhood of $\mathfrak {o}$ . Here, we give a quick description of the technique, a detailed description can be found in [KH95, §17.2] or in [Wil70].

Consider two closed disks $D_1$ and $D_2$ on $\mathbb {T}^2$ centered at $\mathfrak {o}$ such that $\mathfrak {o}\in D_1 \subset \mathring {D}_2$ . On $D_2$ , we consider the local coordinate system $\{x,y\}$ around $\mathfrak {o}$ projected from the coordinates $\{x,y\}$ on $\mathbb {R}^2$ around $(0,0)$ . With respect to those coordinates on $D_2$ , the fixed point $\mathfrak {o}\in \mathbb {T}^2$ is represented by $(0,0)$ . Then we ‘blow-up’ the fixed point $\mathfrak {o}$ using a smooth map $\phi $ as described as follows:

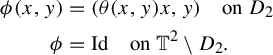$$ \begin{align*} \begin{split} \phi(x,y)&=(\theta(x,y)x, y)\quad \text{on }D_2\\ \phi &= \textrm{Id}\quad \text{on }\mathbb{T}^2\setminus D_2. \end{split} \end{align*} $$

In the above description, $\theta (x,y):\mathbb {T}^2\to [1,\infty )$ is a smooth map such that, on $\mathbb {T}^2\setminus D_2$ , we have $\theta (x,y)=1$ and near the point $\mathfrak {o}$ , the map $\theta (x,y)$ is large enough to counteract the contraction along the x-lines. Then, $\Phi =A \circ \phi $ is a map with a point source at $\mathfrak {o}$ . Notice that the coordinates $(x,y)$ make sense in a neighborhood of $\mathfrak {o}$ , but clearly one cannot have global coordinates in $\mathbb {T}^2$ . Still the equations above make sense.

Property 4.3. [Sma67, Wil70]

The new map satisfies the following properties:

1. (1) $\Phi =A \circ \phi $ is homotopic to A;

2. (2) the maximal invariant set of $\Phi $ consists of a point source and a one-dimensional hyperbolic attractor, denoted by $\Lambda $ ;

3. (3) $A \circ \phi $ preserves the stable foliation $\mathcal {L}^{s}$ of A. More precisely, the attractor of $\Phi $ on $\mathbb {T}^2$ is an attracting hyperbolic set, denoted by $\Lambda $ . This induces a stable foliation in $\mathbb {T}^2 - \mathfrak {o}$ , denoted by $\mathcal {L}^s(\Lambda )$ . The construction is done so that the leaves of $\mathcal {L}^s(\Lambda )$ are contained in leaves of $\mathcal {L}^s$ . Only the stable leaf of $\mathfrak {o}$ is split into two stable leaves of $\mathcal {L}^s(\Lambda )$ . All the other leaves are the same.

Remark 4.4. The usual form of blow-up is to first apply the hyperbolic map A and then the blow-up $\phi $ . It is equivalent to what we do here: the inverse $\Phi ^{-1} = \phi ^{-1} \circ A^{-1}$ and the contraction under $\phi ^{-1}$ in a neighborhood of $\mathfrak {o}$ is stronger than the expansion of $A^{-1}$ . Hence, $\mathfrak {o}$ is an attractor for $\Phi ^{-1}$ and there is a one-dimensional repeller $\Lambda $ for $\Phi ^{-1}$ . Here, $\Lambda $ is the attractor for $\Phi $ . We do it in this form, since it is easier then to prove later on some invariance properties of a metric in which we will be interested.

Remark 4.5. We have described above the DA bifurcation to get a point source. Similarly, we can change the fixed point $\mathfrak {o}$ to a sink. In that case, the maximal invariant set will consist of a point sink and a one-dimensional repeller and the map $A\circ \phi $ would preserve the foliation $\mathcal {L}^u$ .

Next, consider the suspension manifold

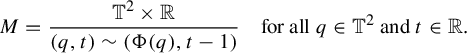$$ \begin{align*}M=\frac{\mathbb{T}^2\times \mathbb{R}}{(q,t)\sim (\Phi(q), t-1)}\quad\text{for all }q\in\mathbb{T}^2\text{ and }t\in\mathbb{R}.\end{align*} $$

The universal cover of M, denoted by $\widetilde {M}$ , is $\mathbb {R}^2\times \mathbb {R}$ equipped with the coordinate system $\{x,y,t\}$ , where the x-axis and y-axis are as described above and the t-axis is in the vertical direction. The vertical lines induce a natural flow $\psi _t$ on M so that its lift $\widetilde \psi _t$ to the universal cover $\widetilde {M}$ is defined by $\psi _t([q,s])=[q,t+s], q \in \mathbb {R}^2$ . Note that we have a periodic orbit $\mathcal {C}$ of $\psi _t$ homeomorphic to the circle inside M through the fixed point $\mathfrak {o}\in \mathbb {T}^2$ .

To construct a hyperbolic plug, we cut out an open solid torus neighborhood $N(\mathcal {C})$ of the periodic orbit $\mathcal {C}$ , the new manifold $M_1=M\setminus N(\mathcal {C})$ is a manifold with boundary and we denote the boundary by $T_1=\partial M_1$ , the boundary is homeomorphic to a 2-torus. We choose $N(\mathcal {C})$ in such a way that the boundary of $N(\mathcal {C})$ is a smooth torus embedded in M and the flow lines of $\psi _t$ transversally intersect the boundary of $N(\mathcal {C})$ . We will have a further condition on $T_1$ described later. Finally, we can restrict the flow $\psi _t$ on $M_1$ , and the restricted semiflow on $M_1$ will be denoted by $\psi ^1_t$ .

It is clear from the construction that $(M_1,\psi ^1_t)$ is an attracting hyperbolic plug as the flow $\phi _t$ is the suspension flow of a ‘DA’ map with an attractor in the maximal invariant set. To ensure that when another plug is attached to $M_1$ along $\partial M_1$ , the semiflows are matched smoothly along the boundary, we attach a collar neighborhood homeomorphic to ${T_1 \times [0,1]}$ along $\partial M_1=T_1$ such that $\partial M_1$ is glued with $T_1\times \{0\}$ . We call the new manifold $\mathcal {M}_1$ , and the boundary component of $\mathcal {M}_1$ is denoted by $\mathcal {T}_1=\partial \mathcal {M}_1$ . Now propagate $\psi ^1_t$ in $T_1\times [0,1]$ via an isotopy such that the extension of the flow on $T_1\times [0,1]$ is a product flow topologically. We denote the extended flow on $\mathcal {M}_1$ by $\Psi ^1_t$ . In the next proposition, we sum up the description of the above construction.

Proposition 4.6. The pair $(\mathcal {M}_1, \Psi ^1_t)$ as constructed above is a hyperbolic plug where $\partial \mathcal {M}_1=\partial ^{in}\mathcal {M}_1$ and its maximal invariant set in $\mathcal {M}_1$ is a hyperbolic attractor. In fact, we can make the blow-up operation on finitely many periodic orbits to obtain an attracting hyperbolic plug with a finite number of boundary components. The stable foliation of the hyperbolic attractor inside $\mathcal {M}_1$ intersects each component of $\partial \mathcal {M}_1$ in a one-dimensional foliation with two Reeb annuli.

If we consider a repelling ‘DA’ map in the previous construction, we would get a repelling hyperbolic plug where the unstable foliation of the repelling set inside $\mathcal {M}_1$ intersects each component of $\partial \mathcal {M}_1$ in a one foliation with Reeb components.

Definition 4.7. Any attracting or repelling plug with finite number of boundary components as constructed in Proposition 4.2 is called a Franks–Williams-type hyperbolic plug in this article.

Remark 4.8. The explicit description of the blow-up is done for the orbit which is the suspension of the point $(0,0)$ . Later, computations and results will be done relative to this orbit. Note that the period of the orbit through $(0,0)$ is one, in particular, the orbit intersects every $\mathbb {T}^2$ -fiber in M only once. Given a different periodic orbit, one can choose a sufficiently large cover to assume that the periodic orbit is of period one. As there are only finitely many orbits which we want to blow-up, we can perform the whole calculation in some n-cover where all the chosen periodic orbits to blow-up are of period one. Working in a finite cover does not affect the proof of the main result because the blow-up maps act locally and at the end, we have to observe it in the universal cover. Hence, the arguments in this article work for any collection of blow-ups as described above. The reason we can find a finite cover that works for all orbits is because the resulting manifold fibers over the circle: we remove finitely many tori neighborhoods of periodic orbits, so the resulting manifold with boundary fibers over the circle. Each of the individual gluings preserves the curve that bounds a fiber on each side; therefore, the resulting manifold fibers over the circle. In the resulting manifold, one can then take a finite cover, so that in the corresponding finite covers in each of the pieces, the fibers cut each of the the associated finitely periodic orbits only once. Notice that the resulting manifold fibers over the circle (as is the case of the Franks and Williams example), but the flow we construct is definitely not a suspension. It is easy to see it is not a suspension because we glue with a time reversal: in the simplest example of Franks and Williams, there are two manifolds, in one of them, the flow is essentially ‘going up’, and in the other one, it is essentially ‘going down’, which implies the flow is not a suspension. In general, the flow is said to be ‘going up’ in the attractors and ‘going down’ in the repellers.

4.2 Construction of the example manifolds and the flows on them

We consider a finite collection of Franks–Williams-type plugs, say

$$ \begin{align*}\{(\mathcal{M}_1,\Psi^1_t);(\mathcal{M}_2,\Psi^2_t);\cdots;(\mathcal{M}_n,\Psi_t^n)\}\end{align*} $$

along with a diffeomorphism $\Omega $ from the collection of exit boundaries $\mathcal {D}^{\mathrm {out}}=\sqcup _1^n\partial ^{\mathrm {out}}_i$ to the collection of entrance boundaries $\mathcal {D}^{in}=\sqcup _1^n\partial ^{in}_i$ . In this notation, for any plug $(\mathcal {M}_i,\Psi ^i_t)$ , either $\partial ^{\mathrm {out}}_i$ or $\partial ^{in}_i$ is empty, and the other one is non-empty. If $\partial ^{in}_i$ is non-empty, then it may have more than one component, each homeomorphic to a 2-torus, and the weak-stable foliation $\mathcal {L}^{ws}(\Lambda _i)$ of the semiflow $\Psi _t^i$ intersects each component of $\partial ^{in}_i$ in a union of two Reeb annuli. Similarly, if $\partial ^{\mathrm {out}}_i\neq \emptyset $ , each component of $\partial ^{\mathrm {out}}_i$ intersects the weak-unstable foliation $\mathcal {L}^{wu}(\Lambda _i)$ in a one-dimensional foliation with two Reeb annuli.

Using the diffeomorphism $\Omega $ , we can construct the manifold

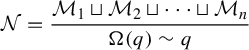$$ \begin{align*}\mathcal{N}=\frac{\mathcal{M}_1\sqcup \mathcal{M}_2\sqcup\cdots\sqcup \mathcal{M}_n}{\Omega(q)\sim q}\end{align*} $$

and the semiflows $\{\Psi ^1_t,\Psi ^2_t,\ldots ,\Psi ^n_t\}$ match to produce a flow $\Psi _t$ on $\mathcal {M}$ . If we consider a diffeomorphism $\Omega : \mathcal {D}^{\mathrm {out}}\rightarrow \mathcal {D}^{in}$ that transversally maps the one-foliation on each component of $\partial ^{\mathrm {out}}_i$ to the one-foliation on the respective component of $\mathcal {D}^{in}$ , then by Proposition 4.2, the flow $\Psi _t$ on $\mathcal {N}$ is Anosov.

Definition 4.9. An Anosov flow constructed in the way described above from Franks–Williams-type plugs will be called generalized Franks–Williams (GFW) flow in this article.

The original construction by Franks and Williams was to construct a hyperbolic plug $(\mathcal {M}_1,\Psi ^1_t)$ from a DA map and with one exit boundary component, and attach it with $(\mathcal {M}_1,\Psi ^1_{-t})$ (that is, the same manifold equipped with the reversed flow) along the boundaries with a $\pi /2$ -rotation.

5 Riemannian metric on the plugs and the whole manifold

To analyze quasigeodesic behavior of the flow lines, we will first define a suitable Riemannian metric on our manifold. As $\mathcal {N}$ is a compact manifold, for any two Riemannian metrics $\tilde {g}_1$ and $\tilde {g}_2$ on the universal cover $\widetilde {\mathcal {N}}$ (which project down on $\mathcal {N}$ ), the identity map on $\widetilde {\mathcal {N}}$ is a quasi-isometry with respect to the induced path metrics. As quasigeodesic behavior is a property that is invariant under quasi-isometries, it is enough to work with one fixed metric.

We construct a Riemannian metric $\mathcal {G}_i$ on the hyperbolic plugs $\mathcal {M}_i$ for each i, and then attach them along the boundary components of the $\mathcal {M}_i$ using the map $\Omega $ to construct the metric $\mathcal {G}$ on the whole manifold $\mathcal {M}$ . We describe the details of the construction of the Riemannian metric $\mathcal {G}_1$ on $\mathcal {M}_1$ and the same process works for all other plugs $\mathcal {M}_i$ .

5.1 Construction of a Riemannian metric $\mathcal {G}_1$ on $\mathcal {M}_1$

Consider the attracting DA map $\Phi :\mathbb {T}^2\rightarrow \mathbb {T}^2$ and the manifold $M=\mathbb {T}^2\times [0,1]/\sim $ as described in the previous section. The universal cover of M, $\widetilde {M}=\mathbb {R}^2\times \mathbb {R}$ , is equipped with the coordinate system $\{x,y,t\}$ . The lift of the flow $\psi _t$ to the universal cover $\widetilde {\mathcal {M}}=\mathbb {R}^2\times \mathbb {R}$ will be henceforth denoted by $\widehat {\psi }_t$ (we explain the $\widehat { }$ notation later). We can also define a three-frame $\{\mathscr {X},\mathscr {Y},\mathscr {T}\}$ on the tangent bundle $T(\mathbb {R}^2\times \mathbb {R})$ , where the vector fields $\mathscr {X}$ , $\mathscr {Y}$ , and $\mathscr {T}$ are parallel to the x-direction, y-direction, and t-direction, respectively. In addition, we define the vector field $\mathscr {T}$ as $\mathscr {T}=({d}/{dt})\widehat {\psi }_t$ .

Remark 5.1. The y-direction on $\mathbb {R}^2$ is parallel to the strong unstable foliation of $\widetilde {A}$ on $\mathbb {R}^2$ , but the blow-up does not preserve the unstable direction. Hence, the y-direction does not represent the unstable leaves of the attractor of the $DA$ -map $\widetilde {A}\circ \tilde {\phi }$ , though the x-direction is parallel to the stable leaves of the attractor.

We first construct a metric on M and then restrict it to $M_1=M\setminus N(\mathcal {C})$ . Our convention is that $M_1$ is the complement of the interior of $N(\mathcal {C})$ in M, so $M_1$ is compact and with boundary. We will use an intermediate cover of $M_1$ which will be denoted by $\widehat {M}_1$ . Consider the repelling periodic orbit $\mathcal {C}$ of $\psi _t$ in M and $N(\mathcal {C})$ a solid torus neighborhood of $\mathcal {C}$ as described in §3.1. Let $\widehat {N(\mathcal {C})}$ be the collection of lifts of $N(\mathcal {C})$ in $\widetilde {M} = \mathbb {R}^2\times \mathbb {R}$ . Then define $\widehat {M}_1=(\mathbb {R}^2\times \mathbb {R})\setminus \widehat {N(\mathcal {C})}$ , again the convention is that we are removing the interior of the sets. In other words, $\widehat {M}_1$ is the pullback of $M_1$ under the cover $\widetilde M \to M$ . This is an infinite cover of $M_1=M\setminus N(\mathcal {C})$ , but it is not the universal cover of $M_1$ . Later in this article, we do much of the analysis in $M_1$ and $\widehat {M}_1$ instead of $\widetilde {M}$ . For this reason, we will denote the metrics using the hat notation.

If $\widehat {G}_1$ is a Riemannian metric on $\widetilde {M}$ which projects down to M, then the deck transformations on $\widetilde {M}=\mathbb {R}^2\times \mathbb {R}$ have to be isometries with respect to $\widehat {G}_1$ . The deck transformation group on $\widetilde {M}$ is generated by the following diffeomorphisms:

1. (1) $\Gamma : \mathbb {R}^2\times \mathbb {R} \rightarrow \mathbb {R}^2\times \mathbb {R}$ ,

   $$ \begin{align*}\Gamma(x,y,t)=(\widetilde{\Phi}(x,y), t-1),\end{align*} $$
   where $\widetilde {\Phi }(x,y)$ is the lift of the map $\Phi =A\circ \phi $ from $\mathbb {T}^2$ to $\mathbb {R}^2$ so that $\widetilde {\Phi }(0,0) = (0,0)$ ;

2. (2) translations by one unit in two horizontal directions with respect to the Euclidean coordinate system on $\mathbb {R}^2\times \mathbb {R}$ , that is:

   1. (a) $E_1(e_1, e_2,t)=(e_1+1, e_2,t)$ ;

   2. (b) $E_2(e_1, e_2,t)=(e_1, e_2+1,t)$ ,

   where $e_1$ and $e_2$ are given with respect to the Euclidean co-ordinates on $\mathbb {R}^2\times \mathbb {R}$ .

It is enough to construct the metric $\widehat {G}_1$ on $\mathbb {R}^2\times [0,1]$ such that the maps

$$ \begin{align*}\Gamma:\mathbb{R}^2\times\{1\}\rightarrow \mathbb{R}^2\times \{0\}, \ \ \Gamma(x,y,1)=(\widetilde{\Phi}(x,y),0)=(\tilde{A}\circ \tilde{\phi}(x,y),0)\end{align*} $$

and the translations $E_1$ and $E_2$ restricted on $\mathbb {R}^2\times [0,1]$ are isometries. Notice that the first map is between two-dimensional sets, and the other two are between three-dimensional sets.

As before, we consider the coordinate system $\{x,y,t\}$ on $\mathbb {R}^2\times [0,1]$ . The idea to define the metric on $\mathbb {R}^2\times [0,1]$ is as follows. We will pick a suitable metric $g_0$ on the level $t = 0$ and consider a family $h_s$ of maps, smoothly varying with $s\in [0,1]$ , where $h_0=\textrm {Id}$ and $h_1=\widetilde {\Phi }$ . Then we will pull-back the metric $g_0$ from the level $\{t=0\}$ to the level $\{t=s\}$ via the map $h_s$ .

First, we define a family of maps on $\mathbb {R}^2$ . Consider the neighborhood $D_2$ with the local co-ordinate system $\{x,y\}$ as defined in the description of the DA map in the previous section. Let $\widetilde {\theta }$ be the lift to $\mathbb {R}^2$ of $\theta : \mathbb {T}^2 \to \mathbb {R}$ . Now define the family of maps ${\tilde {\eta }_s:\mathbb {R}^2\rightarrow \mathbb {R}^2}$ for $s\in [0,1]$ as follows. First define

$$ \begin{align*}B_s(x,y) \ = \ (\lambda^{-s} x, \lambda^s y).\end{align*} $$

Notice that $B_1 = \widetilde {A}$ . Also define

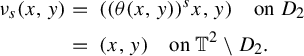$$ \begin{align*} \begin{split} \nu_s(x,y) &= \ ((\theta(x,y))^s x, y)\quad \text{on }D_2\\ &= \ (x,y)\quad \text{on }\mathbb{T}^2\setminus D_2. \end{split} \end{align*} $$

Again notice that $\nu _1 = \phi $ . Let $\tilde {\nu }_s: \mathbb {R}^2 \to \mathbb {R}^2$ be the lift of $\nu _s$ so that $\tilde {\nu }_s(0,0) = (0,0)$ . Then define

$$ \begin{align*}\tilde{\eta}_s(x,y) = B_s \circ \tilde{\nu}_s (x,y).\end{align*} $$

Now we are ready to define the family of maps $h_s:\mathbb {R}^2\times \{s\}\rightarrow \mathbb {R}^2\times \{0\}$ :

$$ \begin{align*}h_s(x,y,s)=(\tilde{\eta}_s(x,y),0)\quad\text{for }s\in[0,1].\end{align*} $$

In general, it is not easy to find the exact formula of the lifts $\tilde {\eta }_s$ , except near the point $(0,0)$ , where it is easy to get an explicit formula.

For each s, the map $h_s$ takes the level $\mathbb {R}^2 \times \{ s \}$ to $\mathbb {R}^2 \times \{ 0 \}$ . We start with the metric $g_0^2=dx^2+dy^2$ on the level $\mathbb {R}^2\times \{0\}$ where $dx$ (respectively $dy$ ) measures the length along x-directions (respectively y-directions).

Using the family $h_s, 0 \leq s \leq 1$ , we can pull-back the metric $g_0^2=dx^2+dy^2$ from $\mathbb {R}^2\times \{0\}$ to each level $\mathbb {R}^2 \times \{ s \}$ . Hence, on $\mathbb {R}^2\times \{t\}$ , we define the pull-back metric $g_t=(h_t)^*(g_0)$ , where $t\in [0,1]$ .

With the induced differentiable structure in $\mathbb {R}\times [0,1]$ from inclusion in $\mathbb {R}^2\times \mathbb {R}$ , it is easy to see that the the metrics on $\mathbb {R}\times \{t\}$ vary smoothly with $t\in [0,1]$ because of the smoothness of family $h_s, 0 \leq s \leq 1$ . We now define a metric not only on horizontal vectors, but on all vectors. At the point $q=(q_1,t)\in \mathbb {R}^2\times [0,1]$ , the metric is defined as follows:

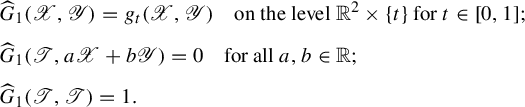(5.4) $$ \begin{align} &\widehat{G}_1(\mathscr{X},\mathscr{Y}) = g_t(\mathscr{X},\mathscr{Y}) \quad\text{on the level }\mathbb{R}^2\times\{t\}\text{ for }t\in[0,1]; \nonumber\\[4pt] & \widehat{G}_{1}(\mathscr{T}, a\mathscr{X}+b\mathscr{Y})= 0\quad\text{for all }a,b\in\mathbb{R};\nonumber\\[4pt] & \widehat{G}_1(\mathscr{T},\mathscr{T})= 1. \end{align} $$

Observation 5.2. Then metric $\widehat {G}_1$ on $\mathbb {R}^2\times [0,1]$ as defined above in §5.1 is invariant under the maps $\Gamma $ , $E_1$ , and $E_2$ as follows:

1. (1) clearly the map $\Gamma :\mathbb {R}^2\times \{1\}\rightarrow \mathbb {R}^2\times \{0\}$ defined by $\Gamma (x,y,1)=(\tilde {A}\circ \tilde {\phi }(x,y),0)$ is an isometry as

   $$ \begin{align*}\widehat{G}_1|_{\mathbb{R}^2\times\{1\}}=(\tilde{A}\circ \tilde{\phi})^*(\widehat{G}_1|_{\mathbb{R}^2\times\{0\}});\end{align*} $$

2. (2) on the level $\mathbb {R}^2\times \{0\}$ , the metric $g_0^2=dx^2+dy^2$ is invariant under the translations. On each level $\mathbb {R}^2\times \{t\}$ , the metric $(h_t)^*(g_0)$ can be written as

   $$ \begin{align*}(B_t \circ \tilde{\nu_t})^*(g_0) \ = \ (\tilde{\nu}_t)^* ((B_t)^* (g_0)).\end{align*} $$

   Notice first that $B_t$ does not leave invariant the integer lattice. However, $(B_t)^*$ leaves invariant the metric—-it is the Solv metric in this setting. It is clear that $\tilde {\nu _t}$ leaves invariant the metric under integer translations, since it came from a map in $\mathbb {T}^2$ . The $B^*_t$ invariance of $g_0$ was the reason for choosing $\Phi = A \circ \phi $ , rather than $\phi \circ A$ .

   It follows that the translations $E_1$ and $E_2$ are isometries with respect to the pull-back metrics on each level $\mathbb {R}^2\times \{t\}$ .

Definition 5.3. The description of the metric $\widehat {G}_1$ on $\mathbb {R}^2\times [0,1]$ as in §5.1 together with Observation 5.2 defines a metric on M. We denote this metric on M by $G_1$ .

Restrict the metric $G_1$ on $M_1=M\setminus N(\mathcal {C})$ .

Before describing the metric on the whole manifold $\mathcal {N}$ , we prove the following lemma, whose proof is simple but crucial, derived from the above defined Riemannian metric on $(\mathcal {M}_1,\mathcal {G}_1)$ .

Remark 5.4. We start with the flow $\psi _1$ in $M_1$ or M. In the following proof and in the other situations in this article, we analyze flow lines in the lift $\widehat {M}_1$ . This is contained in the universal cover $\widetilde {M}$ . Some arguments are done in $\widetilde {M}$ . For simplicity of notation, we denote the lift of $\psi _t$ to $\widehat {M}_1$ and the lift of $\psi _t$ to $\widetilde {M}$ by the same notation $\widehat {\psi }_t$ .

Lemma 5.5. If $\gamma $ is a flow line or flow ray of $\psi _t$ contained in $M_1$ , then the lift of $\gamma $ in the universal cover $\widetilde {M}_1$ is a globally length minimizing geodesic.

Proof. Consider the universal cover $\widetilde {M}=\mathbb {R}^2\times \mathbb {R}$ with the metric $\widehat {G}_1$ and the subset $\widehat {M}_1$ contained in it. It is enough to prove that the flow lines or flow rays in $\widehat {M}_1$ are length minimizing in $\widehat {M}_1$ with respect to $\widehat {G}_1$ . This is because any rectifiable curve $\gamma $ in $\widetilde {M}_1$ joining two points in a flow line or flow ray in $\widetilde {M}_1$ projects to a curve in $\widehat {M}_1$ joining two points in a flow line or flow ray.

What we prove is that the flow lines in $\widetilde {M}$ are globally length minimizing. This implies that that the flow lines or flow rays contained in $\widehat {M}_1$ are length minimizing in $\widehat {M}_1$ . Notice also that we denote the flows in $\widetilde {M}$ or $\widehat {M}_1$ by $\widehat {\psi }_t$ , see previous remark.

We note that the flow lines of the suspension flow $\widehat {\psi }_t$ in $\widetilde {M}=\mathbb {R}^2\times \mathbb {R}$ are the vertical lines $\{*\}\times \mathbb {R}$ in $\mathbb {R}^2\times \mathbb {R}$ . These lines are the integral curves of the vector field ${\mathscr {T}=({d}/{dt})\widehat {\psi }_t}$ in $\mathbb {R}^2\times \mathbb {R}$ . As the vectors in the t-directions are orthogonal to the vectors in the span of $\{\mathscr {X},\mathscr {Y}\}$ (that is, in the horizontal levels $\mathbb {R}^2\times \{t\}$ ), the integral curves of the vector field $\mathscr {T}=({d}/{dt})\widehat {\psi }_t$ are globally length minimizing. More precisely, consider a vertical line $\{a\}\times \mathbb {R}$ and take two points $p_1$ and $p_2$ on it. Suppose $\sigma $ is a curve connecting $p_1$ and $p_2$ , then

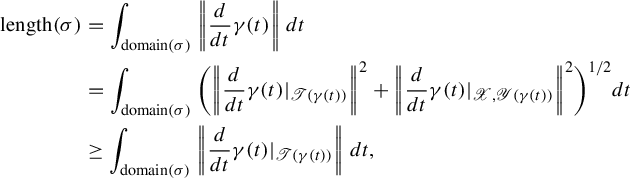$$ \begin{align*} \begin{aligned} \text{length}(\sigma) & =\int_{\text{domain}(\sigma)}\bigg\|\frac{d}{dt}\gamma(t)\bigg\|\,dt \\ & =\int_{\text{domain}(\sigma)}\bigg(\bigg\|\frac{d}{dt}\gamma(t)|_{\mathscr{T}(\gamma(t))}\bigg\|^2+\bigg\|\frac{d}{dt}\gamma(t)|_{\mathscr{X},\mathscr{Y}(\gamma(t))}\bigg\|^2\bigg)^{1/2}dt\\ & \geq \int_{\text{domain}(\sigma)}\bigg\|\frac{d}{dt}\gamma(t)|_{\mathscr{T}(\gamma(t))}\bigg\|\,dt, \end{aligned} \end{align*} $$

where $({d}/{dt})\gamma (t)|_{\mathscr {T}(\gamma (t))}$ and $({d}/{dt})\gamma (t)|_{\mathscr {X},\mathscr {Y}(\gamma (t))}$ denote the components of $\gamma '(t)=({d}/{dt})\gamma (t)$ along the t-direction and in the span of $\{\mathscr {X},\mathscr {Y}\}$ , respectively. Hence, it is clear that the integral curves of the vector field $\mathscr {T}=({d}/{dt})\widehat {\psi }_t$ , that is, the flow lines of $\widehat {\psi }_t$ in $\mathbb {R}^2\times \mathbb {R}$ , are globally length minimizing geodesic in $\widehat {M}=\mathbb {R}^2\times \mathbb {R}$ with respect to the metric $\widehat {G}_1$ .

As the flow lines of $\widehat {\psi }_t$ in $\widetilde {\mathcal {M}}$ are length minimizing geodesic, so is the flow lines or flow rays of the restricted flow $\widehat {\psi }_t|_{\widehat {M}_1}$ on $\widehat {M}_1$ inside $\widetilde {\mathcal {M}}$ .

Note that $\widehat {M}_1$ is not the universal cover of $M_1$ , but an infinite subcover of $M_1$ . As the flow rays are globally length minimizing geodesic in a subcover, the same has to be true in the universal cover $\widetilde {M}_1$ . This completes the proof.

We end this subsection with a crucial remark which will be used later.

Remark 5.6. The construction of our metric $G_1$ is motivated by the Solv metric ${dS^2=\lambda ^{-2s}\,dx^2+\lambda ^{2s}\,dy^2+ds^2}$ on $\mathbb {R}^2\times \mathbb {R}$ . We observe that there is another way to see the metric $\widehat {G}_1$ on $M_1$ , we can find a map $\mathcal {H}$ such that the family of map $h_s$ can be written as $h_s=\overline {B}_s\circ \mathcal {H}$ , where $\overline {B}_s(x,y,s)=(\lambda ^{-s}x,\lambda ^s y,0)$ . To see that such an $\mathcal {H}$ exists, it is enough to determine the map near the t-axis and it is easy to check that the map $\mathcal {H}(x,y,s)=((\tilde {\theta }(x,y))^s x,y,s)$ near $\{(0,0,t)|t\in \mathbb {R}\}$ serves the purpose. We can extend it to all of $\widetilde {M}$ using the definition of $\theta $ in $\mathbb {T}^2$ . Hence, the pull-back metric on the level $\mathbb {R}^2\times \{s\}$ is the same with $\mathcal {H}^*( \overline {B}_s^*(g_0))$ .

If we consider the family of pull-back metrics $\overline {B}_s^*(g_0)$ where $g_0^2=dx^2+dy^2$ on the level $\mathbb {R}^2\times \{0\}$ , it is easy to check that we get the Solv metric $dS$ on $\widetilde {\mathcal {M}}=\mathbb {R}^2\times \mathbb {R}$ ,

$$ \begin{align*}dS^2=\lambda^{-2s}\,dx^2+\lambda^{2s}\,dy^2+dt^2\quad\text{for }s\in[0,1].\end{align*} $$

Hence, the metric we defined, $\widehat {G}_1=\mathcal {H}^*(dS)$ , is a bounded perturbation of the Solv metric on each level $\mathbb {R}^2\times \{s\}$ .

5.2 Defining the metric on the whole manifold

As before, we consider a collection of attracting and repelling Franks–Williams-type hyperbolic plugs

$$ \begin{align*}\{(\mathcal{M}_1,\Psi_t^1);(\mathcal{M}_2,\Psi_t^2);(\mathcal{M}_3,\Psi_t^3);\cdots;(\mathcal{M}_n,\Psi_t^n\}.\end{align*} $$

By our construction, we have a metric $G_i$ on $M_i\subset \mathcal {M}_i$ for each i. The (possibly disconnected) surface $\partial M_1$ is smooth in the metric in M and hence inherits a Riemannian metric. Now, we smoothly extend the metrics $G_i$ on the union collar neighborhoods $\bigcup _i \partial M_i\times [0,1]$ to get a Riemannian metric $\widetilde {\mathcal {G}}$ on the whole manifold $\widetilde {\mathcal {N}}$ , in particular, $\widetilde {\mathcal {G}}|_{M_i}=G_i$ for all i. Note that there are only finitely many collar neighborhoods in $\bigcup _i \partial M_i\times [0,1]$ . Any flowline which enters in a collar neighborhood exits it after a finite time. Hence, the length of any flow segment contained in a collar neighborhood is bounded above by a global upper bound. For this reason, the choices of metrics on the collar neighborhoods do not affect the quasigeodesic behavior.

Remark 5.7. The manifolds $\mathcal {M}_i$ have boundary which is $\pi _1$ -injective in $\mathcal {N}$ for any i, because each boundary component of each $\mathcal {M}_i$ is $\pi _1$ -injective in $\mathcal {M}_i$ . It follows that any lift of $\mathcal {M}_i$ to the universal cover $\widetilde {\mathcal {N}}$ is itself a universal cover of $\mathcal {M}_i$ . So we can think of these lifts as copies $\widetilde {\mathcal {M}}_i$ of the universal cover of $\mathcal {M}_i$ which are contained in $\widetilde {\mathcal {N}}$ .

The restriction of $\widetilde {\mathcal {G}}$ to a lift $\widetilde {\mathcal {M}}_i$ of a single hyperbolic plug is denoted by $\widetilde {\mathcal {G}}_i$ , and the path metric induced by $\widetilde {\mathcal {G}}_i$ on $\widetilde {\mathcal {M}}_i$ is denoted by $d_{\widetilde {\mathcal {G}}_i}$ .

Notation:

• • for any $\mathcal {M}_i$ , $\mathcal {G}|_{\mathcal {M}_i} =\mathcal {G}_i$ ;

• • for any two points $p_1$ and $p_2$ in $\widetilde {\mathcal {M}}_i$ ,

  $$ \begin{align*}d_{\widetilde{\mathcal{G}}_i}(p,q)=\text{minimum}\{\text{length}_{\widetilde{\mathcal{G}}_i}(\sigma)|\sigma\text{ is a curve contained in }\widetilde{\mathcal{M}}_i\text{ connecting }p_1,p_2\}.\end{align*} $$

We finish this section showing that the flow lines or flow rays contained in the lift $\widetilde {\mathcal {M}}_i$ of a single hyperbolic plug in the universal cover $\widetilde {\mathcal {N}}$ is a quasigeodesic with respect to the restricted metric $d_{\widetilde {\mathcal {G}}_i}$ .

Lemma 5.8. There is an $\epsilon \geq 1$ and $\epsilon '\geq 0$ such that if $\gamma $ is a flow ray or flow line fully contained in some $\widetilde {\mathcal {M}}_i$ , and $p_1$ , $p_2$ are two points on $\gamma \subset \widetilde {\mathcal {M}}_i$ , then

$$ \begin{align*}\text{length}_{\widetilde{\mathcal{G}}_i}(\gamma_{[p_1,p_2]})\leq \epsilon d_{\widetilde{\mathcal{G}}_i}(p_1,p_2)+\epsilon'.\end{align*} $$

Proof. Without loss of generality, we prove the lemma in $\widetilde {\mathcal {M}}_1$ . As both $M_1$ and $\mathcal {M}_1$ are compact and the metric $G_1$ is the restriction of the metric $\mathcal {G}_1$ on $M_1$ , it is easy to check that $(\widetilde {M_1},d_{\widetilde {G}_1})$ is quasi-isometric to $(\widetilde {\mathcal {M}}_1, d_{\widetilde {\mathcal {G}}_1})$ . Hence, there exists $\epsilon _1\geq 1$ and $\epsilon _2 \geq 0$ such that for any $p_1,\ p_2\in \widetilde {M}_1$ ,

$$ \begin{align*} \begin{split} \text{length}_{\widetilde{\mathcal{G}}_1}(\gamma_{[p_1,p_2]})&=\text{length}_{\widetilde{G}_1}(\gamma_{[p_1,p_2]}) \quad\text{as }\widetilde{G}_1=\widetilde{\mathcal{G}}_1|_{\widetilde{M_1}}\\ &=d_{\widetilde{G}_1}(\gamma_{[p_1,p_2]}) \quad\text{by Lemma 5.5}\\ &\leq \epsilon_1 d_{\widetilde{\mathcal{G}}_1}(p_1,p_2)+\epsilon_2 \quad\text{as }(\widetilde{M}_1,d_{\widetilde{G}_1})\text{ is quasi-isometric to}(\widetilde{\mathcal{M}}_1,d_{\widetilde{\mathcal{G}}_1}).\\ \end{split} \end{align*} $$

Now, we assume that $p_2\in \widetilde {\mathcal {M}}_1\setminus \widetilde {M}_1$ and $p_1 \in \widetilde {M}_1$ .

Here, $\widetilde {\mathcal {M}}_1$ can be written as $\widetilde {M_1}\cup (\partial \widetilde {M}_1\times [0,1])$ . By the compactness of $\partial M_1\times [0,1]$ , we can consider $\epsilon _3>0$ such that for any flow ray $\gamma $ ,

$$ \begin{align*}\text{length}_{\widetilde{\mathcal{G}}_1}(\gamma\cap (\partial \widetilde{M}_1\times [0,1]))\leq \epsilon_3.\end{align*} $$

Now consider the flow segment $\gamma _{[p_1,p_2]}$ , as $p_2\in \widetilde {\mathcal {M}}_1\setminus \widetilde {M}_1$ , the flow segment must intersect $\partial \widetilde {M}_1$ at a single point, say $p_3$ . Then,

$$ \begin{align*} \begin{split} \text{length}_{\widetilde{\mathcal{G}}_1}(\gamma_{[p_1,p_2]})&=\text{length}_{\widetilde{\mathcal{G}}_1}(\gamma_{[p_1,p_3]})+\text{length}_{\widetilde{\mathcal{G}}_1}(\gamma_{[p_3,p_2]})\\ &\leq \epsilon_1 d_{\widetilde{\mathcal{G}}_1}(\gamma_{[p_1,p_3]})+\epsilon_2+\text{length}_{\widetilde{\mathcal{G}}_1}(\gamma_{[p_3,p_2]})\quad\text{as }p_1,p_3\in \widetilde{M}_1\\ & \leq \epsilon_1 d_{\widetilde{\mathcal{G}}_1}(p_1,p_3)+\epsilon_2+\epsilon_3\\ &\leq \epsilon_1 (d_{\widetilde{\mathcal{G}}_1}(p_1,p_2)+d_{\widetilde{\mathcal{G}}_1}(p_2,p_3))+\epsilon_2+\epsilon_3\\ &\leq \epsilon_1 (d_{\widetilde{\mathcal{G}}_1}(p_1,p_2)+\epsilon_3)+\epsilon_2+\epsilon_3 \quad\text{as }p_2,p_3\in\partial\widetilde{M}_1\times [0,1]\\ & \leq \epsilon_1 d_{\widetilde{\mathcal{G}}_1}(p_1,p_2)+\epsilon_1\epsilon_3+\epsilon_2+\epsilon_3. \end{split} \end{align*} $$

We redefine $\epsilon _1$ and $\epsilon _1\epsilon _3+\epsilon _2+\epsilon _3$ as $\epsilon $ and $\epsilon '$ .

As there are only finitely many plugs, we can choose $\epsilon $ and $\epsilon '$ big enough such that it works for all $\partial \widetilde {M}_i\times [0,1]$ and the result follows.

6 Analysis of the flowlines

In this section, we show that every flow line of the flow $\widetilde {\Psi }_t$ on $\widetilde {\mathcal {N}}$ is quasigeodesic with respect to the path metric induced by Riemannian metric $\widetilde {\mathcal {G}}$ as constructed in the previous section. As before, $\mathcal {N}$ is made of the collection of hyperbolic plugs

$$ \begin{align*}\{(\mathcal{M}_1, \Psi_t^1, \mathcal{G}_1);(\mathcal{M}_2, \Psi_t^2, \mathcal{G}_2);(\mathcal{M}_3, \Psi_t^3, \mathcal{G}_3);\cdots;(\mathcal{M}_n, \Psi_t^n, \mathcal{G}_n)\}.\end{align*} $$

First, we consider a single hyperbolic plug, say $(\mathcal {M}_1,\Psi ^1_t, \mathcal {G}_1)$ , and analyze the properties of the flow lines of the semi-flow $\Psi ^1_t$ .

6.1 Flowlines in the plug $(\mathcal {M}_1,\mathcal {G}_1,\Psi ^{1}_t)$

Recall that $\mathcal {M}_1$ is made from $M=({\mathbb {T}^2\times \mathbb {R}})/{(q,t)\sim (\Phi (q),t-1)}$ as in §4.1, where $\Phi =A \circ \phi $ is a repelling DA map. The universal cover $\widetilde {M}$ can be considered as $\mathbb {R}^2\times \mathbb {R}$ equipped with the coordinate system $\{x,y,t\}$ , where x-directions and y-directions are parallel to the strong stable and the strong unstable directions of the hyperbolic map $\widetilde {A}$ on $\mathbb {R}^2$ and t-directions are along the flow lines of the suspension flow $\widehat {\psi }^1_t$ .

Consider the repelling periodic orbit $\mathcal {C}$ of $\psi _t$ in M and $N(\mathcal {C})$ is an open solid torus neighborhood of $\mathcal {C}$ as described in §3.1. Let $\widehat {N(\mathcal {C})}$ be the collection of lifts of $N(\mathcal {C})$ in $\mathbb {R}^2\times \mathbb {R}$ , then $\widehat {M}_1=(\mathbb {R}^2\times \mathbb {R})\setminus \widehat {N(\mathcal {C})}$ is an infinite cover of $M_1=M\setminus N(\mathcal {C})$ , but not the universal cover.

Here, $M_1$ is equipped with the Riemannian metric $G_1$ as constructed in the previous section, similarly, we denote the lifted metric on $\widehat {M}_1$ by $\widehat {G}_1$ .

Additionally, $\widehat {M}_1$ is a manifold with boundary, where $\partial \widehat {M}_1$ is the lift of $\partial {M_1}=T_1$ . Furthermore, $\partial \widehat {M}_1$ is a collection of disjoint infinite cylinders in $\mathbb {R}^2\times \mathbb {R}$ which are transverse to the flow lines. Suppose $\partial \widehat {M}_1=\bigcup _{i\in \mathbb {N}}\widehat {T}_i$ , where $\widehat {T}_i$ are the infinite cylindrical boundary components of $\partial \widehat {M}_1$ .

There are exactly two types of flow lines of the lifted semiflow $\widehat {\psi }^1_t|_{\widehat {M}_1}$ in $\widehat {M}_1$ ; if $\gamma $ is a flow line in $\widehat {M}_1$ , then:

1. (1) either $\gamma $ is contained in $\widehat {\mathcal {A}}$ , the lift of the attractor $\mathcal {A}\subset M_1$ ;

2. (2) or $\gamma $ intersects a lift of $\partial M_1=T_1$ . Moreover, $\gamma $ intersects exactly one such lift of $T_1$ .

Remark 6.1. In the rest of this section, we will mostly deal with $M_1$ and $\mathcal {M}_1$ . For simplicity of notation, we denote the restricted flows $\psi ^1_t$ and $\Psi ^1_t$ by $\psi _t$ and $\Psi _t$ , respectively.

In this subsection, we show that almost all flow rays which intersect the boundary $\partial \widehat {M}_1$ ‘go away’ from the boundary component it intersects in an efficient manner as time t goes to positive infinity. In the next subsection, we extend the result in the universal cover $\widetilde {\mathcal {M}}_1$ . To state the precise statement, we first need to fix some notation.

Consider the repelling fixed point $\mathfrak {o}$ of the DA map $\Phi =A \circ \phi $ on $\mathbb {T}^2$ . There are also two hyperbolic fixed points, denoted by $p_1$ and $p_2$ , on the attractor in $\mathbb {T}^2$ , as shown in Figure 1(a). In the suspension manifold $M=\mathbb {T}^2\times [0,1]/\sim $ , there are two periodic orbits, $C_{p_1}$ and $C_{p_2}$ , coming from $p_1$ and $p_2$ , and these two orbits are contained in the attractor $\mathcal {A}$ of $\psi ^1_t$ . Now we consider the repelling orbit $\mathcal {C}$ and the open solid torus neighborhood $N(\mathcal {C})$ around it, as described in §3.1. The weak stable leaves of $C_{p_1}$ and $C_{p_2}$ intersect the boundary torus $T_1=\partial N(\mathcal {C})=\partial M_1$ in two circles, denoted by $\mathcal {C}_1$ and $\mathcal {C}_2$ , as shown in Figure 1(b).

Definition 6.2. Take a point $q\in \widehat {M}_1$ such that the flow line $\gamma _q$ through q intersects $\partial \widehat {M}_1$ at exactly one point. The boundary component is denoted by $\widehat {T}_q$ .

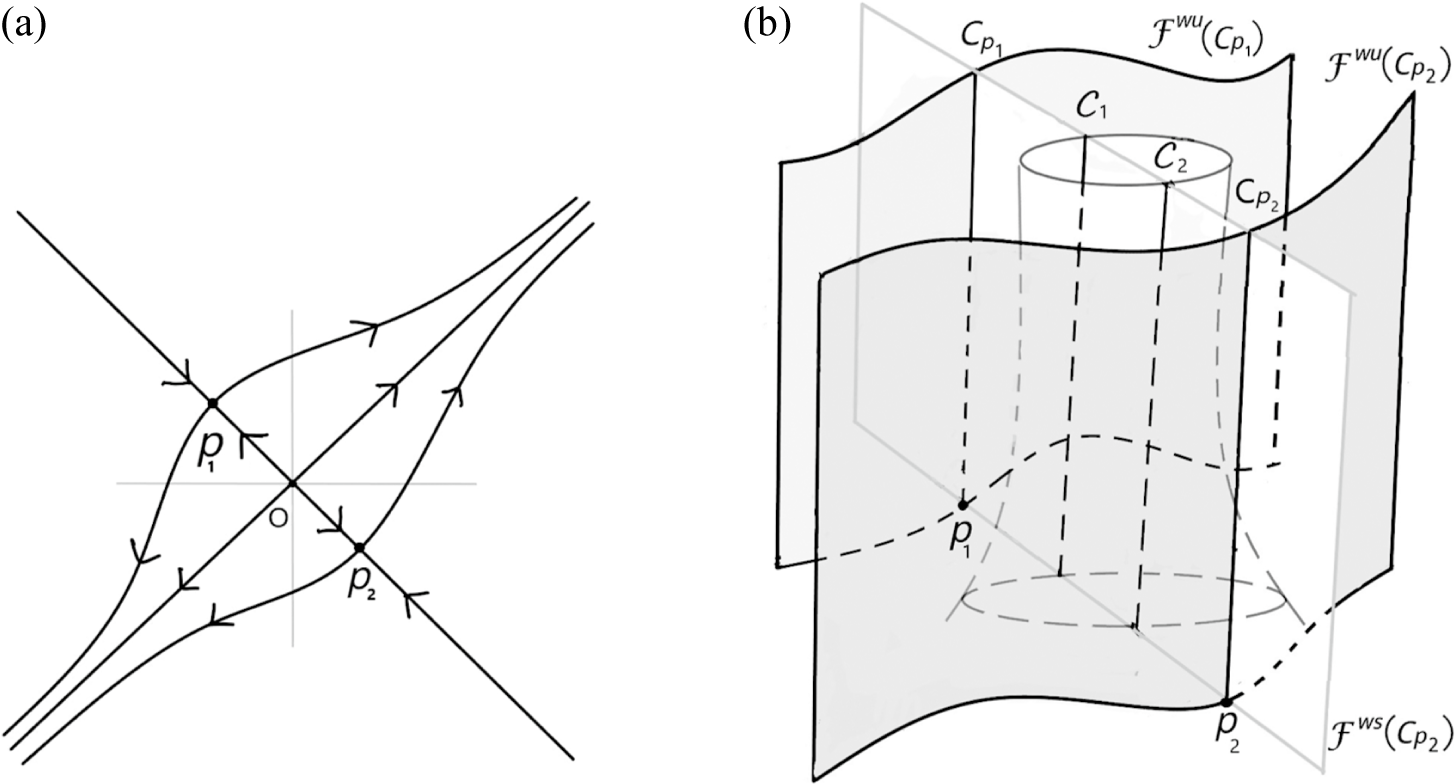
Figure 1 (a) Two-dimensional image of the blow up of a hyperbolic point, here ‘O’ denotes the origin. (b) Three-dimensional image of the blow-up of a hyperbolic orbit.

Then, let:

• • $\mathcal {D}_{\widehat {G}_1}(q,\widehat {T}_q)$ (respectively $\mathcal {D}_{S}(q,\widehat {T}_q)$ ) denote the distance between q and $\widehat {T}_q$ with respect to the path metric induced by $\widehat {G}_1$ (respectively the Solv metric $dS$ ) on $\widehat {M}_1$ ;

• • $\ell _{\widehat {G}_1}(q)$ (respectively $\ell _{S}(q)$ ) is the length of the flow line segment connecting q and $\widehat {T}_q$ with respect to $\widehat {G}_1$ (respectively $dS$ ).

Next, we fix a small number $\delta>0$ and consider the open $\delta $ -neighborhood $N_{\delta }(\mathcal {C}_1\cup \mathcal {C}_2)$ on $T_1$ and let $N_{\delta }(\widehat {\mathcal {C}}_1\cup \widehat {\mathcal {C}}_2)$ denote the lift of $N_{\delta }(\mathcal {C}_1\cup \mathcal {C}_2)$ in $\widehat {M}_1$ . Notice that $\widehat {\mathcal {C}}_1\cup \widehat {\mathcal {C}}_2$ is a countable, infinite collection of properly embedded lines in $\widehat {M}_1$ . The following is a key technical result used in this article.

Proposition 6.3. There exists $C> 1$ and $c> 0$ satisfying the following. Let $q\in \widehat {M}_1$ such that the flow ray through q intersects $\partial \widehat {M}_1$ , say at the boundary component $\widehat {T}_q$ . If $\gamma _q$ intersects $\widehat {T}_q$ on the region $\widehat {T}_q\setminus N_{\delta }(\widehat {\mathcal {C}}_1\cup \widehat {\mathcal {C}}_2)$ , then

$$ \begin{align*}\ell_{\widehat{G}_1}(q)\leq C\mathcal{D}_{\widehat{G}_1}(q, \widehat{T}_q) +c.\end{align*} $$

Proof. We will prove the lemma in the manifold $\widetilde {M}=\mathbb {R}^2\times \mathbb {R}$ using the coordinate system $\{x,y,t\}$ on it. This is enough, because we have $\widehat {M}_1\subset \widetilde {M}=\mathbb {R}^2\times \mathbb {R}$ and the distance between two points in $\widehat {M}_1$ with respect to the metric $d_{\widehat {G}_1}$ is bigger than the distance in $\mathbb {R}^2\times \mathbb {R}$ with respect to $d_{\widehat {G}}$ . In addition, the length of a flow segment is the same in both $\widehat {M}_1$ and $\widetilde {M} = \mathbb {R}^2\times \mathbb {R}$ , as the Riemannian metric in $\widehat {M}_1$ is the one induced from the inclusion $\widehat {M}_1 \subset \widetilde {M} = \mathbb {R}^2\times \mathbb {R}$ .

It is enough to prove the result for one component of the boundary $\partial \widehat {M}_1$ as we can permute the boundary components using the translation isometries. In addition, up to changing the coordinates $(x,y)$ , we can assume the orbit passes through $(0,0,0)$ . In other words, we fix the lift of the repelling orbit $\mathcal {C}$ passing through $(0,0,0)\in \mathbb {R}^2\times \mathbb {R}$ , that is, the line $\{(0,0,t)|t\in \mathbb {R}\}$ and the lift of the $\partial M_1=T_1$ around this line, which we denote by  $\widehat {T}_0$ .

We will first prove the result for the points q on the $yt$ -plane $\{x=0\}$ . The reason behind it is that the Riemannian metric on the $yt$ -plane is almost $\lambda ^{2t}\,dy^2+dt^2$ . We make this more precise in the following remark.

Remark 6.4.

1. (1) Note that the map $\tilde {\phi }:\mathbb {R}^2\rightarrow \mathbb {R}^2$ perturbs the y-directions only near the lifts in $\mathbb {R}^2$ of the repelling fixed point $\frak {o}$ , and outside of those neighborhoods, the map $\widetilde {\phi }$ is the identity map. Hence, it is also true that that map $\mathcal {H}$ distorts the $yt$ -plane boundedly in $\mathbb {R}^2\times \mathbb {R}$ . By Remark 5.6, we know that $\widehat {G}_1=\mathcal {H}^{*}(dS)$ , where $dS$ is the Solv metric. In particular, the Solv metric restricted on the $yt$ -plane is $\lambda ^{2t}\,dy^2+dt^2$ , and the x-directions are everywhere perpendicular to the $yt$ -plane. Hence, we can assume that the Riemannian metric on the $yt$ -plane induced by $\widehat {G}_1$ is boundedly distorted from and very close to the Solv metric. In other words, we can find two constants $a_0>1$ and $a_1>0$ such that if $\sigma $ is a curve on the $yt$ -plane, then

   $$ \begin{align*}\frac{1}{a_0}\text{length}_{\widehat{G}_1}(\sigma)-a_1\leq\text{length}_{S}(\sigma)\leq a_0\text{ length}_{\widehat{G}_1}(\sigma)+a_1,\end{align*} $$
   where $\text {length}_S(\sigma )$ and $\text {length}_{\widehat {G}_1}(\sigma )$ mean the length of $\sigma $ with respect to the Solv metric $dS$ and $\widehat {G}_1$ , respectively.

2. (2) Note that the $yt$ -plane is the unstable leaf through $(0,0,0)$ for the suspension of the linear Anosov map $\tilde {A}$ . Notice that the $yt$ -plane is not invariant under the map $\widetilde {A}\circ \widetilde {\phi }$ .

Now we can state the precise result we want to prove on the $yt$ -plane.

Lemma 6.5. There exists $K>1$ and $k>0$ such that for any q in the intersection of the $yt$ -plane with $\widehat {M}_1$ for which the flow line $\gamma _q$ intersects $\widehat {T}_0$ , we have

$$ \begin{align*}\ell_{\widehat{G}_1}(q)\leq K\mathcal{D}_{\widehat{G}_1}(q, \widehat{T}_0)+k.\end{align*} $$

Proof. Consider a point q on the $yt$ -plane such that the flow ray $\gamma _q$ passing through q intersects $\widehat {T}_0$ .

As the manifolds are complete, every distance can be realized by a curve. Suppose $\sigma :[0,1]\rightarrow \widetilde {M}$ denotes a shortest path connecting q and $\widehat {T}_0$ in $\widehat {M}_1$ .

Claim 6.6. Any shortest path $\sigma $ between q and $\widehat {T}_0$ lies on the $yt$ -plane.

Proof. Suppose $\sigma $ is parameterized as $\sigma (t)=(\sigma _1(t),\sigma _2(t),\sigma _3(t))$ in $\mathbb {R}^2\times \mathbb {R}$ . Consider the projection of $\sigma $ on the $yt$ -plane, $\Pi (\sigma (t))=(0,\sigma _2(t),\sigma _3(t))$ . Suppose $\Pi (\sigma (a))$ is the first intersection point of $\Pi (\sigma )$ and $\widehat {T}_0$ . We show that

$$ \begin{align*}\text{length}(\Pi(\sigma))|_{[0,a]}\leq \text{length}(\sigma)\end{align*} $$

and the claim follows from that.

In Remark 5.6, we have seen that the metric $\widehat {G}_1$ can be expressed as the pull-back of the Solv metric $dS$ by the map $\mathcal {H}$ , that is, $\widehat {G}_1=\mathcal {H}^*(dS)$ , where ${dS=\lambda ^{-2s}\,dx^2+\lambda ^{2s}\,dy^2+dt^2}$ .

Consider the map $\mathcal {H}:\mathbb {R}^2\times \mathbb {R}\rightarrow \mathbb {R}^2\times \mathbb {R}$ as in Remark 5.6. As $\widehat {G}_1=\mathcal {H}^*(dS)$ , for any curve $\zeta $ ,

$$ \begin{align*}\text{length}(\zeta)\text{ with respect to the metric }\widehat{G}_1=\text{length}(\mathcal{H}(\zeta))\text{ with respect to the metric }dS.\end{align*} $$

As the directions x, y, and t are orthogonal to each other with respect to the Solv metric $dS$ , it is easy to check that for any curve $\zeta $ in $\mathbb {R}^2\times \mathbb {R}$ and its projection $\Pi (\zeta )$ on $yt$ -plane, we have

$$ \begin{align*}\text{length}(\Pi(\delta))\leq \text{length}(\sigma)\text{ with respect to the metric }dS.\end{align*} $$

Moreover, the projection map $\Pi $ commutes with $\mathcal {H}$ because $\mathcal {H}$ does not change the y-coordinate of a point and $\Pi $ is the projection on the $yt$ -plane. This can also be easily verified by the formulas.

Hence, we conclude

$$ \begin{align*} & \text{length}(\Pi(\mathcal{H}(\sigma)))\leq \text{length}(\mathcal{H}(\sigma))\text{ with respect to the metric }dS \\ \implies &\text{length}(\mathcal{H}(\Pi(\sigma)))\leq \text{length}(\mathcal{H}(\sigma))\text{ with respect to the metric }dS \\ \implies &\text{length}(\Pi(\sigma)))\leq \text{length}(\sigma)\text{ with respect to the metric }\widehat{G}_1. \end{align*} $$

This completes the claim.

In the rest of the proof of Lemma 6.5, we will use the Solv metric on the $yt$ -plane, that is, the metric $\lambda ^{2t}\,dy^2+dt^2$ for simplicity of calculations. In Remark 5.2, we have seen that the Solv metric on the $yt$ -plane is quasi-isometric to the metric induced by $\widehat {G}_1$ .

Consider the point $q=(0,c,0)$ with $c>0$ on the $\widehat {T}_0\cap yt$ -plane and the forward flow ray $\gamma _{q}=\widetilde {\psi }^1_{[0,\infty )}(p)$ , as shown in Figure 2, $\gamma _q=\{(0,c,t)|t\in [0,\infty )\}$ .

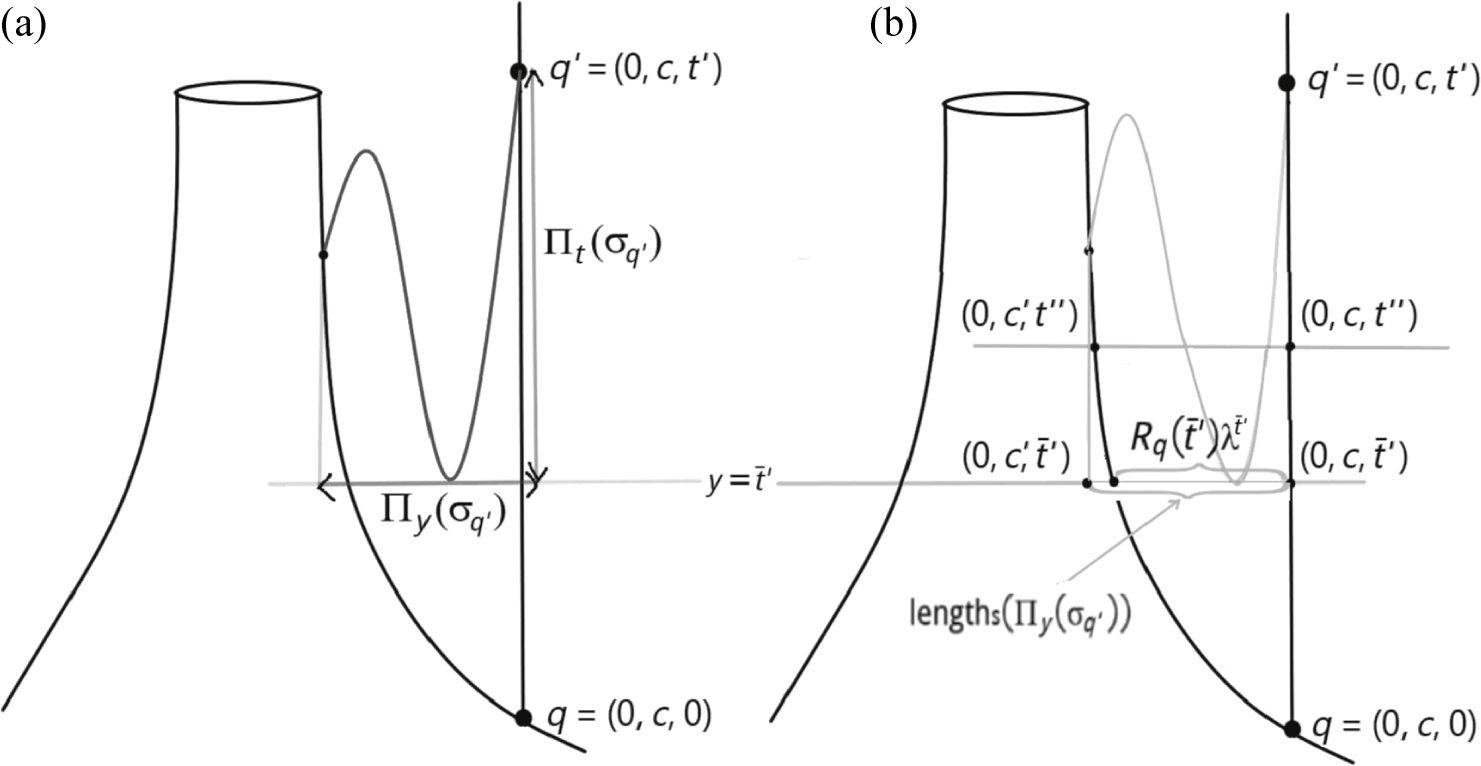
Figure 2 (a) A minimal path in the $yt$ -plane from $q'$ to the lift of the boundary torus and (b) several geometric quantities that are used in the analysis. In particular, $R_q(\overline {t}') \lambda ^{\overline {t}'}$ is the length in the solvable metric of the horizontal segment depicted at height $\overline {t}'$ .

We prove the lemma for the flow ray $\gamma _q$ first. Later, we explain how to derive the result for all other flow lines in the $yt$ plane intersecting $\widehat {T}_0$ from this particular result on $\gamma _q$ .

Proof for the flow line $\boldsymbol {\gamma _q}$ : suppose $q'=(0,c,t')$ is a point on $\gamma _q$ and let $\sigma _{q'}$ be a length minimizing curve on the $yt$ -plane joining $q'$ and $\widehat {T}_0$ . We define three functions as follows.

1. (1) Let $\Pi _t(\sigma _{q'})$ denote the projection of $\sigma _{q'}$ on the vertical line $\gamma _q=\{(0,c,t)|t\in \mathbb {R}\}$ along y-directions—same as horizontal directions (notice that $\sigma _{q'}$ is contained in the $yt$ plane).

2. (2) Suppose $\bar {t'}$ is the lowest t-value attained by the curve $\sigma _{q'}$ as shown in Figure 2(a). Then we denote the projection of $\sigma _{q'}$ on the line $t=\bar {t'}$ along t-directions—same as vertical directions—by $\Pi _y(\sigma _{q'})$ .

3. (3) For a point $(0,c,t")$ on $\gamma _{q'}$ , suppose the line $t=t"$ intersects $\widehat {T}_0$ in the positive side of y-direction at $(0,c',t")$ as shown in Figure 2(b). Then we define $R_{q}(t")=|c-c'|$ . Note that, with respect to the Solv metric $dS$ , the length of the segment on the line $t=t"$ connecting $(0,c,t")$ and $(0,c',t")$ is $\lambda ^{t"}|c-c'|$ or $R_{q}(t")\lambda ^{t"}$ . Clearly, $R_{q}$ is an increasing function of t on $[0,\infty )$ .

Now we are ready to state two lower estimates of $\mathcal {D}_{S}(q',\widehat {T}_0)$ .

Claim 6.7. Suppose $\bar {t'}$ is the lowest t-value in the projection $\Pi _t(\sigma _{q'})$ as shown in Figure 2(a). Then:

1. (1) $t'-\bar {t'}\leq \mathcal {D}_{S}(q',\widehat {T}_0)$ ;

2. (2) in addition, $R_{q}(\bar {t'})\lambda ^{\bar {t'}}\leq \mathcal {D}_{S}(q',\widehat {T}_0)$ .

Proof. As the t-directions and y-directions are everywhere orthogonal with respect to the metric $\lambda ^{2t}\,dy^2+dt^2$ , it is easy to check that $\text {length}_{S}(\Pi _t(\sigma _{q'}))\leq \text {length}_{S}(\sigma _{q'})$ and, in addition, we have $\text {length}_S(\Pi _y(\sigma _{q'}))\leq \text {length}_S(\sigma _{q'})=\mathcal {D}_S(q',\widehat {T}_0)$ .

1. (1) As the curve $\Pi _t(\sigma _{q'})$ connects the points $q'=(0,c,t')$ and $(0,c,\bar {t'})$ , it is clear that $|t'-\bar {t'}|\leq \text {length}_S(\Pi _t(\sigma _{q'}))\leq \mathcal {D}_{S}(q',\widehat {T}_0)$ .

   Note that $\bar {t'}$ cannot be a negative number, because if $\bar {t'}<0$ , then

   $$ \begin{align*}t'-\bar{t'}>t'=\ell_S(q')\geq \mathcal{D}_{S}(q',\widehat{T}_0),\end{align*} $$
   which cannot be true as we have just proved $t'-\bar {t'}\leq \mathcal {D}_{S}(q',\widehat {T}_0)$ .

2. (2) As $\bar {t'}\geq 0$ , we observe that the line segment $\{(0,y,\bar {t'})|y\in [c-R_{q}(\bar {t'}),c]\}$ is contained in the curve $\Pi _y(\sigma _{q'})$ as shown in Figure 2(b). Hence,

   $$ \begin{align*}R_{q}(\bar{t'})\lambda^{\bar{t'}}\leq\text{length}_S(\Pi_t(\sigma_{q'}))\leq\text{length}_S(\sigma_{q'}) =\mathcal{D}_{S}(q',\widehat{T}_0).\end{align*} $$

This proves the claim.

Consider the function $P_{q}(t)={R_{q}({t}/{2})\lambda ^{{t}/{2}}}/{t}$ on $t\in (0,\infty )$ .

As the function $R_{q}(t/2)$ is increasing and $\lambda ^{t/2}/t$ is strictly increasing for large t values, we can fix a value $k'>0$ such that $P_{q}(t)>1$ when $t>k'$ .

For the point $q'=(0,c,t')$ , if $t'>k'$ , then $R_q(t'/2)\lambda ^{t'/2}>t'$ . However, $t'=\ell _{S}(q')\geq \mathcal {D}_{S}(q',\widehat {T}_0)$ . Combining these two inequalities, we get

(6.5) $$ \begin{align} \mathcal{D}_{S}(q',\widehat{T}_0)\leq \ell_{S}(q')=t' < R_{q}(t'/2)\lambda^{t'/2}. \end{align} $$

Hence, by Claim 6.7(2), $t'/2$ cannot be smaller than the lowest t-value attained by the curve $\Pi _t(\sigma _{q'})$ , that is, $t'/2>\bar {t'}$ . Otherwise, we get

$$ \begin{align*}R_{q}(t'/2)\lambda^{t'/2}\leq R_{q}(\bar{t'})\lambda^{\bar{t'}}\leq \mathcal{D}_{S}(q',\widehat{T}_0),\end{align*} $$

which contradicts equation (6.5).

Finally, as $t'/2>\bar {t'}$ , applying Claim 6.7(1), we deduce

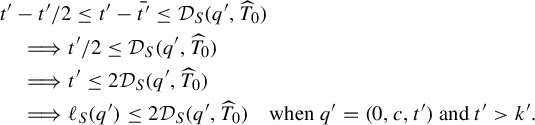(6.6) $$ \begin{align} &t'-t'/2\leq t'-\bar{t'}\leq \mathcal{D}_{S}(q',\widehat{T}_0)\nonumber\\ &\quad\!\implies\! t'/2\leq \mathcal{D}_{S}(q',\widehat{T}_0) \nonumber\\ &\quad\!\implies\! t'\leq 2\mathcal{D}_{S}(q',\widehat{T}_0)\nonumber\\ &\quad\!\implies\! {\ell_S(q')\leq 2\mathcal{D}_{S}(q',\widehat{T}_0)\quad\text{when }q'=(0,c,t')\text{ and }t'>k'.} \end{align} $$

If $t'\leq k'$ , then for a point $q'=(0,c,t')$ , we get

(6.7) $$ \begin{align} \ell_{S}(q')\leq k'\leq k'+2\mathcal{D}_{S}(q',\widehat{T}_0). \end{align} $$

Combining equations (6.6) and (6.7), we conclude

(6.8) $$ \begin{align} \ell_{S}(q')\leq2\mathcal{D}_{S}(q',\widehat{T}_0)+k'\quad\text{for all } q'\in\gamma_q=\{(0,c,t)|t\in[0,\infty)\}. \end{align} $$

Finally, by using Remark 6.4, we can deduce $\mathcal {D}_{S}(q',\widehat {T}_0)\leq a_0\mathcal {D}_{\widehat {G}}(q',\widehat {T}_0)+a_1$ and replacing it in the previous equation,

$$ \begin{align*}\ell_{S}(q')&\leq2\mathcal{D}_{S}(q',\widehat{T}_0)+k'\\&\leq 2a_0\mathcal{D}_{\widehat{G}_1}(q',\widehat{T}_0)+2a_1+k'\quad\text{for all } q'\in\gamma_q=\{(0,c,t)|t\in[0,\infty)\}.\end{align*} $$

By renaming $2a_0=K$ and $2a_1+k'=k$ , and replacing $\ell _{S}(q')=\ell _{\widehat {G}_1}(q')$ ,

$$ \begin{align*}{\ell_{\widehat{G}_1}(q')\leq K\mathcal{D}_{\widehat{G}_1}(q',\widehat{T}_0)+k\quad\text{for all } q'\in\gamma_q=\{(0,c,t)|t\in[0,\infty)\}.}\end{align*} $$

This completes the proof of Lemma 6.5 only on the flow ray $\gamma _q$ , where $q=(0,c,0)$ . To deal with the other flow rays in the $yt$ -plane, we do the following: consider a family of maps

$$ \begin{align*}\mu_a: \widetilde{M} \to \widetilde{M},\quad \mu_a(x,y,t) = (\lambda^a x, \lambda^{-a} y, t + a),\end{align*} $$

where a is an arbitrary real number. It is easy to see that any $\mu _a$ is an isometry of the Solv metric $dS$ . In addition, we choose the original torus $T_0$ transverse to the flow so that $\mu _a$ leaves invariant the fixed lift $\widehat {T}_0$ of $T_0$ to $\widetilde {M}$ for any $a \in \mathbb {R}$ . Notice that $\mu _a$ also fixes the $yt$ plane. In the $yt$ plane, $\mu _a$ sends flow lines to flow lines. If $p = \mu _a(q)$ , then p is also in $\widehat {T}_0$ . Now for any $p'$ in the forward flow line of p, one obtains equation (6.8) for $p'$ as well, since $\mu _a$ is an isometry of the Solv metric. This obtains all flow lines in the $yt$ -plane, except for the flow line through $(0,0,0)$ , but this one does not intersect $\widehat {T}_0$ . Now use Remark 6.4 to finish the proof of Lemma 6.5.

Now we are ready to prove Proposition 6.3.

Proof of Proposition 6.3

The maximal invariant set of the semiflow $\psi ^1_t$ is a hyperbolic set $\mathcal {A}$ in $M_1$ , which is a two-dimensional attractor. Consider the weak-stable foliation $\mathcal {L}^{ws}$ of $\mathcal {A}$ associated with the semiflow $\psi ^1_t$ in $M_1$ . Every point in $M_1$ is in $\mathcal {L}^{ws}$ , as every point in $M_1$ is attracted to $\mathcal {A}$ . The foliation $\mathcal {L}^{ws}$ intersects the boundary $\partial M_1$ in a one-dimensional foliation which has two Reeb components [FW80]; we denote this foliation on $\partial M_1$ by $\mathcal {F}$ . As described before, the circular leaves of $\mathcal {F}$ are denoted by $\mathcal {C}_1$ and $\mathcal {C}_2$ . They are the common boundary circles of the Reeb annuli of $\mathcal {F}$ .

Suppose $\widehat {\mathcal {F}}$ is the lift of $\mathcal {F}$ on $\widehat {T}_0$ . The intersection of the $yt$ -plane and $\widehat {T}_0$ has two components, say $D_1$ and $D_2$ , as shown in Figure 3. Here, $\widehat {\mathcal {C}}_1$ and $\widehat {\mathcal {C}}_2$ are on two different sides of the $yt$ -plane. As any leaf L of $\widehat {\mathcal {F}}$ (except $\widehat {\mathcal {C}}_1$ and $\widehat {\mathcal {C}}_2$ ) is asymptotic to both $\widehat {\mathcal {C}}_1$ and $\widehat {\mathcal {C}}_2$ , it must intersect the $yt$ -plane in a single point either on $D_1$ or on $D_2$ , as shown in Figure 3.

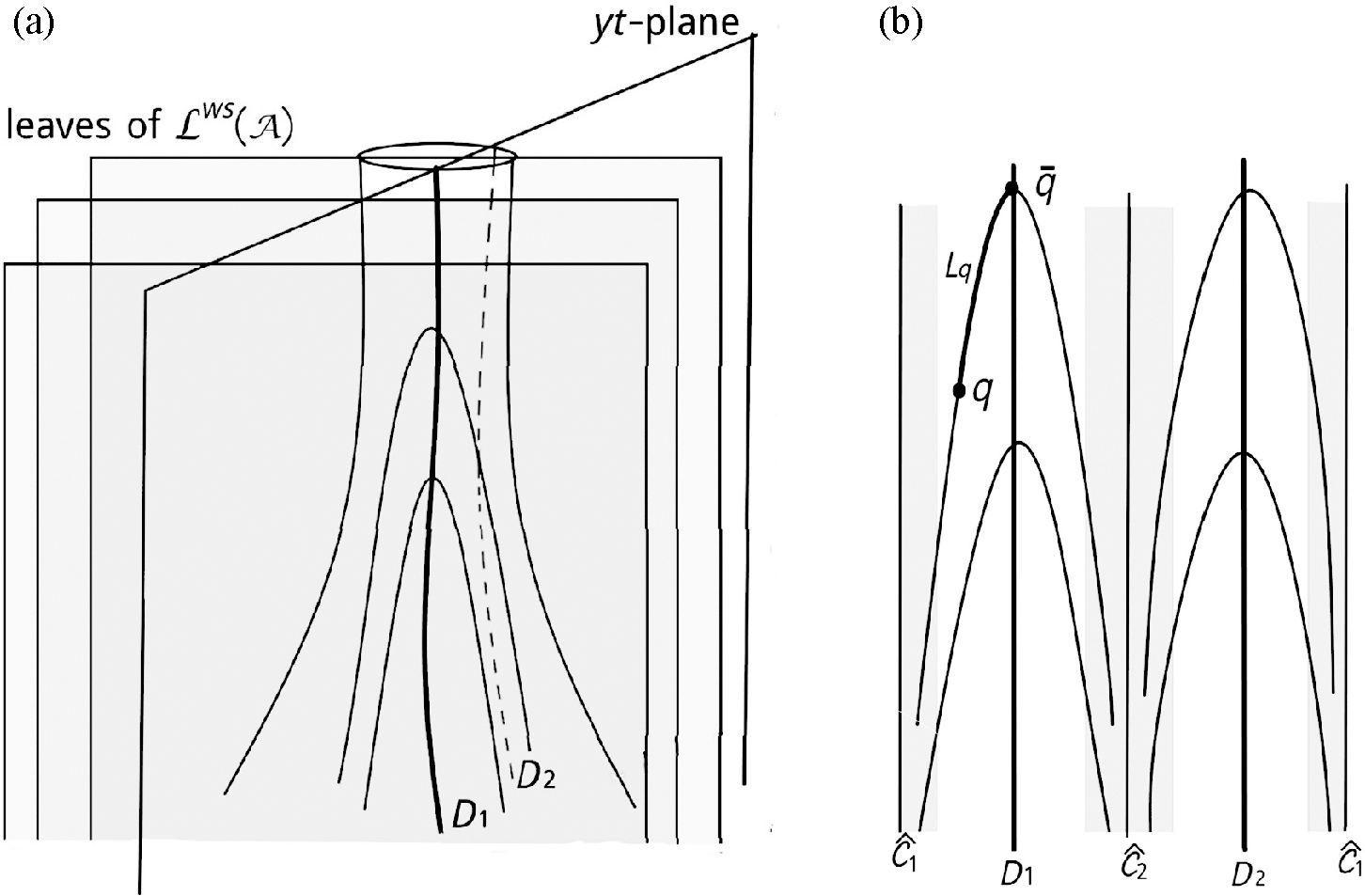
Figure 3 (a) Foliation $\widehat {\mathcal {F}}$ in a lift of a torus; (b) leaf of $\widehat {\mathcal {F}}$ through q intersects $D_1$ at $\bar {q}$ . The shaded region represents the ‘bad region’.

Consider $q\in \widehat {T}_0\setminus \{\widehat {\mathcal {C}}_1, \widehat {\mathcal {C}}_2\}$ and the leaf $L_q$ of $\widehat {\mathcal {F}}$ passing through q. As described above, $L_q$ intersects either $D_1$ or $D_2$ at a single point, without loss of generality we assume that $L_q$ intersects $D_1$ and let $\bar {q}=D_1\cap L_q$ , as shown in Figure 3. Note that q and $\bar {q}$ lie on the same leaf of the weak stable foliation of $\widehat {\mathcal {A}}$ , and hence there exists $s\in \mathbb {R}$ such that $\widehat {\psi }^1_s(q)$ and $\bar {q}$ lie on the same strong stable leaf of $\hat {\psi }^1_t$ . It follows that

$$ \begin{align*}d_{\widehat{G}_1}(\widehat{\psi}^1_{t+s}(q),\widehat{\psi}^1_t(\bar{q}))\to 0\quad\text{as }t\to \infty.\end{align*} $$

Let $s_1 = d_{\widehat {G}_1}(q,\bar {q})$ . Fix $\delta _1>0$ , $\delta _1 << 1, \delta _1 < s_1$ . By the above limit, we can find ${s_2>0}$ such that $d_{\widehat {G}_1}(\widehat {\psi }^1_{t+s}(q),\widehat {\psi }^1_t(\bar {q}))\leq \delta _1$ whenever $t>s_2$ .

For any $t'>s_2$ , consider the four points $q,q_{t'}=\widehat {\psi }^1_{t'+s}(q),\bar {q}$ and $\bar {q}_{t'}=\widehat {\psi }^1_{t'}(\bar {q})$ . By the triangle inequality,

(6.9) $$ \begin{align} d_{\widehat{G}_1}(q,q_{t'})\leq d_{\widehat{G}_1}(q,\bar{q})+d_{\widehat{G}_1}(\bar{q},\bar{q}_{t'})+d_{\widehat{G}_1}(\bar{q}_{t'},q_{t'}). \end{align} $$

Note that $d_{\widehat {G}_1}(q,q_{t'})=\ell _{\widehat {G}_1}(q_{t'})$ as q and $q_{t'}$ lie on the same flow ray and by Lemma 5.5, flow segments are length minimizing in $\widehat {M}$ with respect to the path metric of $\widehat {G}_1$ , similarly $d(\bar {q},\bar {q}_{t'})=\ell _{\widehat {G}_1}(q_{t'})$ . Moreover, by our assumption, $d_{\widehat {G}_1}(q,\bar {q}) = s_1$ , $d_{\widehat {G}_1}(q_{t'},\bar {q}_{t'})<\delta _1$ . Replacing in the above inequality (6.9), we get

(6.10) $$ \begin{align} \ell_{\widehat{G}_1}(q_{t'}) & \leq d_{\widehat{G}_1}(q,\bar{q})+d_{\widehat{G}_1}(\bar{q},\bar{q}_{t'})+d_{\widehat{G}_1}(\bar{q}_{t'},q_{t'}) \nonumber\\ & \leq s_1+\ell_{\widehat{G}_1}(\bar{q}_{t'})+\delta_1\nonumber\\ & = \ell_{\widehat{G}_1}(\bar{q}_{t'})+2s_1\quad\text{for any }t'>s_2. \end{align} $$

As $\bar {q}\in \widehat {T}_0\cap \{yt\}-$ plane, by Lemma 6.5, we know there are global $K, k> 0$ , so that $\ell _{\widehat {G}_1}(\bar {q}_{t'})\leq K\mathcal {D}_{\widehat {G}_1}(\bar {q}_{t'},\widehat {T}_0)+k$ . Applying it in equation (6.10), we have

(6.11) $$ \begin{align} \ell_{\widehat{G}_1}(q_{t'})\leq \ell_{\widehat{G}_1}(\bar{q}_{t'})+2s_1 \leq K\mathcal{D}_{\widehat{G}_1}(\bar{q}_{t'},\widehat{T}_0)+k+2s_1 \quad \text{when }t'>s_2. \end{align} $$

Finally, suppose $a\in \widehat {T}_0$ is a point in $\widehat {T}_0$ that is closest to $q_{t'}$ , that is, $d_{\widehat {G}_1}(q_{t'},a)=\mathcal {D}_{\widehat {G}_1}(q_{t'},\widehat {T}_0)$ . By the triangle inequality, we get $d_{\widehat {G}_1}(\bar {q}_{t'},a)\leq d_{\widehat {G}_1}(q_{t},a)+d_{\widehat {G}_1}(q_{t'},\bar {q}_{t'})$ . Moreover, $\mathcal {D}_{\widehat {G}_1}(\bar {q}_{t'},\widehat {T}_0)\leq d_{\widehat {G}_1}(\bar {q}_{t'},a)$ as $a\in \widehat {T}_0$ . Combining all these facts, we conclude that when $t'>s_2$ ,

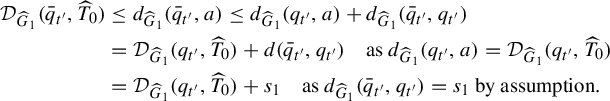(6.12) $$ \begin{align} \mathcal{D}_{\widehat{G}_1}(\bar{q}_{t'},\widehat{T}_0) & \leq d_{\widehat{G}_1}(\bar{q}_{t'},a) \leq d_{\widehat{G}_1}(q_{t'},a)+d_{\widehat{G}_1}(\bar{q}_{t'},q_{t'}) \nonumber\\ &= \mathcal{D}_{\widehat{G}_1}(q_{t'},\widehat{T}_0)+d(\bar{q}_{t'},q_{t'})\quad\text{as }d_{\widehat{G}_1}(q_{t'},a)=\mathcal{D}_{\widehat{G}_1}(q_{t'},\widehat{T}_0)\nonumber\\ &= \mathcal{D}_{\widehat{G}_1}(q_{t'},\widehat{T}_0)+s_1\quad\text{as }d_{\widehat{G}_1}(\bar{q}_{t'},q_{t'}) = s_1 \text{ by assumption}. \end{align} $$

Combining equations (6.11) and (6.12), we get

(6.13) $$ \begin{align} \ell_{\widehat{G}_1}(q_{t'})\leq K\mathcal{D}_{\widehat{G}_1}(\bar{q}_{t'},\widehat{T}_0)+k+2s_1\leq K\mathcal{D}_{\widehat{G}_1}(q_{t'})+Ks_1+k+2s_1\quad\text{when }t'>s_2. \end{align} $$

The above inequality proves Proposition 6.3 for $t'>s_2$ . If $t'\leq s_2$ , then $\ell (q_{t'})=t'<s_2$ . Adding the case when $t'\leq s_2$ in inequality (6.13), we conclude

(6.14) $$ \begin{align} \ell_{\widehat{G}_1}(q_{t'})\leq K\mathcal{D}_{\widehat{G}_1}(q_{t'})+Ks_1+k+2s_1+s_2\quad\text{for all }t'\in[0,\infty). \end{align} $$

By renaming $C=K$ and $c=Ks_1+k+2S_1+s_2$ , we rewrite the above inequality (6.14) as

$$ \begin{align*}{\ell_{\widehat{G}_1}(q_{t'})\leq C\mathcal{D}_{\widehat{G}_1}(q_{t'})+c\quad\text{for all }t'\in[0,\infty),}\end{align*} $$

which completes the proof of Proposition 6.3 for the point q.

We still need to argue why we can find constants $C>1$ and $c>0$ which work for all $q\in \widehat {T}_0\setminus N_{\delta }(\widehat {\mathcal {C}}_1\cup \widehat {\mathcal {C}}_2)$ . We need to find $s_1$ and $s_2$ big enough, such that inequality (6.14) holds for all flow rays intersecting $\widehat {T}_0\setminus N_{\delta }(\widehat {\mathcal {C}}_1\cup \widehat {\mathcal {C}}_2)$ .

Consider a fundamental domain in $\widehat {T}_0$ which quotient downs on the torus in $M_1$ . Without loss of generality, we assume that the fundamental domain is bounded by the planes $t=0$ and $t=1$ , and we call it $\overline {T}_{0,1}$ . Next, we consider the compact set $\mathcal {S}$ which is the closure of the set $\widehat {T}_{0,1}\setminus N_{\delta }(\widehat {\mathcal {C}}_1\cup \widehat {\mathcal {C}}_2)$ .

As $\mathcal {S}$ is compact, it has finite radius with respect to the metric $d_{\widehat {G}_1}$ . Recall the definition of $s_1$ . It is $s_1 = d_{\widehat {G}_1}(q, \bar {q})$ . Here, $\bar {q} = (D_1 \cup D_2) \cap L_q$ , where $L_q$ is a leaf of $\widehat {\mathcal {F}}$ and $D_1 \cup D_2$ are the intersections of the $yt$ -plane with $\widehat {T}_0$ . Since q is in a compact set $\mathcal {S}$ , it follows that $\bar {q}$ is also in a compact set. It follows that $s_1$ is globally bounded.

Now we consider $s_2$ . Given q, the value s was defined so that $\widehat {\psi }^1_s(q)$ and $\bar {q}$ lie in the same strong stable leaf of $\widehat {\psi }^1_t$ . Again, since $\mathcal {S}$ is compact and $\bar {q}$ is in a compact set, it follows that the values of s as a function of q are also globally bounded in $\mathcal {S}$ . Then, there is a global $s_2> 0$ so that $d_{\widehat {G}_1}(\widehat {\psi }^1_{t+s}(q), \widehat {\psi }^1_t(\bar {q})) < \delta _1$ for all $t> s_2$ .

This shows that $s_1, s_2$ can be chosen globally bounded for q in the fundamental domain $\mathcal {S}$ . Since it is a fundamental domain, this shows that $s_1, s_2$ can be chosen globally bounded.

This finishes the proof of Proposition 6.3.

Remark 6.8. The reason behind considering the $\delta $ -neighborhood of $\mathcal {C}_1\cup \mathcal {C}_2$ is to use the compactness of the set $\mathcal {S}$ , the compactness is used to determine the universality of the constants $s_1$ and $s_2$ . Here, $\widehat {T}_{0,1}\setminus {\widehat {\mathcal {C}}_1\cup \widehat {\mathcal {C}}_2}$ is not compact.

Now we extend Proposition 6.3 in the universal cover of $\widetilde {M}_1$ with respect to the lifted Riemannian metric $\widetilde {G}_1$ . Note that $\partial \widetilde {M}_1$ is the lift of the torus $\partial M_1$ , and it is a collection of infinitely many planes homeomorphic to $\mathbb {R}^2$ . We first re-define the notation as follows.

For a point $q\in \widetilde {M}_1$ , suppose the flow line through q intersects a component of $\partial \widetilde {M}$ , say $\widetilde {T}_q$ , then:

• • $\mathcal {D}_{\widetilde {G}_1}(q,\widetilde {T}_q)$ denotes the distance between q and $\widetilde {T}_q$ with respect to the path metric induced by $\widetilde {G}_1$ on $\widetilde {M}_1$ ;

• • $\ell _{\widetilde {G}_1}(q)$ is the length of the flow line segment connecting q and $\widetilde {T}_q$ with respect to $\widetilde {G}_1$ .

Consider the lift of the neighborhood $N_{\delta }(\mathcal {C}_1\cup \mathcal {C}_2)$ in $\widetilde {M}_1$ , we denote it as $N_{\delta }(\widetilde {\mathcal {C}}_1\cup \widetilde {\mathcal {C}}_2)$ . We can restate Lemma 6.3 in $\widetilde {M}_1$ as follows.

Lemma 6.9. There exists $C> 1$ and $c> 0$ satisfying the following. Let $q\in \widetilde {M}_1$ such that the flow ray through q intersects $\partial \widetilde {M}_1$ , say at the boundary component $\widetilde {T}_q$ . If $\gamma _q$ intersects $\widetilde {T}_q$ on the region $\widetilde {T}_q\setminus N_{\delta }(\widetilde {\mathcal {C}}_1\cup \widetilde {\mathcal {C}}_2)$ , then

$$ \begin{align*}\ell_{\widetilde{G}_1}(q)\leq C\mathcal{D}_{\widetilde{G}_1}(q, \widetilde{T}_q) +c.\end{align*} $$

Proof. Note that $\widehat {M}_1$ is an intermediate cover of $M_1$ , and hence $\widetilde {M}_1$ is the universal cover of $\widehat {M}_1$ . For any two points $b_1$ and $b_2$ in $\widetilde {M}_1$ , if $\bar {b}_1,\bar {b}_2 $ denotes the projection of $b_1, b_2$ in $\widehat {M}_1$ , then

$$ \begin{align*}d_{\widehat{G}_1}(\bar{b}_1,\bar{b}_2)\leq d_{\widetilde{G}_1}(b_1,b_2).\end{align*} $$

As $\widetilde {M}_1$ is the universal cover of a compact manifold, for any point $q\in \widetilde {M}_1$ , there exists a point $q^*\in \widetilde {T}_q$ such that $\mathcal {D}_{\widetilde {G}_1}(q,\widetilde {T}_0)=d_{\widetilde {G}_1}(q,q^*)$ . In addition, there is a path in $\widetilde {M}_1$ from q to $q^*$ which realizes this distance. This implies that if $\bar {q}\in \widehat {M}_1$ is the projection of the point $q\in \widetilde {M}_1$ , then $\mathcal {D}_{\widehat {G}_1}(\bar {q},\widehat {T}_q)\leq \mathcal {D}_{\widetilde {G}_1}(q,\widetilde {T}_q)$ . Moreover, the t-directions are unchanged in $\widehat {M}_1$ and $\widetilde {M}_1$ , and hence $\ell _{\widehat {G}_1}(\bar {q})=\ell _{\widetilde {G}_1}(q)$ . Combining all the information, we get

$$ \begin{align*}\ell_{\widetilde{G}_1}(q)=\ell_{\widehat{G}_1}(\bar{q})\leq C\mathcal{D}_{\widehat{G}_1}(\bar{q},\widehat{T}_{\bar{q}})+c\leq C\mathcal{D}_{\widetilde{G}_1}(q,\widetilde{T}_q)+c.\\[-37pt]\end{align*} $$

Now we extend Lemma 6.9 to $\mathcal {M}_1= M_1\cup (\partial {M_1}\times [0,1])$ . The manifold $\mathcal {N}$ is the union of the collection of $\{(\mathcal {M}_1, \Psi _t^1, \mathcal {G}_1);(\mathcal {M}_2, \Psi _t^2, \mathcal {G}_2);(\mathcal {M}_3, \Psi _t^3, \mathcal {G}_3);\cdots ;(\mathcal {M}_n, \Psi _t^n, \mathcal {G}_n)\}$ , where the plugs intersect each other along their boundary components. As described in §4, we extend Riemannian metrics $G_i$ from $M_i$ to $\mathcal {M}_i$ and the extended metric is $\mathcal {G}_i$ . The induced Riemannian metric in $\mathcal {N}$ is $\mathcal {G}$ . In particular,

$$ \begin{align*}\mathcal{G}|_{M_i}=G_{i}|_{M_i}.\end{align*} $$

In the rest of the article, we consider the path metric $d_{\widetilde {\mathcal {G}}}$ induced from the Riemannian metric $\widetilde {\mathcal {G}}$ on the whole manifold $\widetilde {\mathcal {N}}$ . For two points $p_1,p_2\in \widetilde {\mathcal {N}}$ ,

$$ \begin{align*}d_{\widetilde{\mathcal{G}}}(p_1,p_2)=\text{minimum}\{ \text{ length} \ \sigma|\ \sigma\text{ is a path connecting } p_1,p_2\in\widetilde{\mathcal{N}}\}.\end{align*} $$

We extend the flow $\psi ^{i}_t$ from $M_i$ to $\mathcal {M}_i=M_i\cup (\partial M_i\times [0,1])$ as a product flow (topologically) on $\partial M_1\times [0,1]$ , and the extended flow is denoted by $\Psi ^i_t$ . It is clear that the foliation $\mathcal {L}^{ws}(\mathcal {A}_i)\cap \partial M_i$ on $\partial M_i$ also extends to $\partial M_i \times [0,1]$ , and hence to $\partial \mathcal {M}_i$ . The neighborhood $N_{\delta }(\widetilde {\mathcal {C}}_1\cup \widetilde {\mathcal {C}}_2)$ is also carried by the extended flow on the new boundary $\partial \widetilde {\mathcal {M}}_1$ . In the universal cover $\widetilde {\mathcal {N}}$ , we denote this new set by $N^{\prime }_{\delta }(\widetilde {\mathcal {C}}_1\cup \widetilde {\mathcal {C}}_2)$ .

As before, we have the following definition.

Definition 6.10. Suppose $q\in {\widetilde {\mathcal {M}}}_1$ such that the flow line $\gamma _q$ through q intersects $\partial \widetilde {\mathcal {M}}_1$ at the boundary component $\widetilde {\mathcal {T}}_q$ . Then, let:

• • $\mathcal {D}_{\widetilde {\mathcal {G}}}(q,\widetilde {\mathcal {T}}_q)$ denote the distance between q and $\widetilde {\mathcal {T}}_q$ with respect to the path metric induced by $\widetilde {\mathcal {G}}_1$ ;

• • $L_{\widetilde {\mathcal {G}}}(q) = L_{\widetilde {\mathcal {G}}_1}(q)$ denote the length of the flow line segment connecting q and $\widetilde {\mathcal {T}}_q$ with respect to $\widetilde {\mathcal {G}}$ .

Lemma 6.11. Let $q\in \widetilde {\mathcal {M}}_1$ such that the flow line through q intersects $\partial \widetilde {\mathcal {M}}_1$ at the boundary component $\widetilde {\mathcal {T}}_q$ . If $\gamma _q$ intersects $\widetilde {\mathcal {T}}_q$ on the region $\widetilde {\mathcal {T}}_q\setminus N^{\prime }_{\delta }(\widetilde {\mathcal {C}}_1\cup \widetilde {\mathcal {C}}_2)$ , then there exists $C_1>1$ and $c_1$ such that

$$ \begin{align*} L_{\widetilde{\mathcal{G}}}(q)\leq C_1\mathcal{D}_{\widetilde{\mathcal{G}}}(q, \widetilde{\mathcal{T}}_q) +c_1.\end{align*} $$

Moreover, the constants $C_1$ and $c_1$ do not depend on q or $\widetilde {\mathcal {T}}_q$ .

Proof. Again, we will prove the lemma only for a component of $\partial \widetilde {\mathcal {M}}_1$ , which we will denote by $\widetilde {\mathcal {T}}_0$ . The same result holds for all other components of $\partial \widetilde {\mathcal {M}}_i$ .

Since the flow is a product in $\partial M_1 \times [0,1]$ , then up to changing $c_1$ to a bigger constant, we can assume that $q \in \widetilde {M}_1$ .

If $\gamma $ intersects $\widetilde {\mathcal {T}}_0$ , then it also intersects a component $\widetilde {T}_0$ of $\partial \widetilde {M}_1$ , because the flow $\Psi ^1_t$ is a product in $\partial M_1 \times [0,1]$ . As the distances are measured as minimum lengths of paths for both $\widetilde {G}_1$ and $\widetilde {\mathcal {G}}$ , and $\widetilde {\mathcal {G}}|_{\widetilde {M}_1}=\widetilde {G}_1$ , we conclude

$$ \begin{align*}\mathcal{D}_{\widetilde{G}_1}(q,\widetilde{T}_0) < \mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_0).\end{align*} $$

Notice we are assuming that q is in $\widetilde M_1$ . By the compactness of $\partial M_1\times [0,1]$ , we can find $\epsilon _3>0$ (same as in Lemma 5.8) such that for all $\gamma $ which intersect $\widetilde {\mathcal {T}}_0$ , $\text {length}_{\widetilde {\mathcal {G}}}(\gamma \cap (\widetilde {\widehat {T}_0}\times [0,1]))\leq \epsilon _3$ .

Fix a flow ray $\gamma $ , suppose $\gamma $ intersects $\widetilde {T}_0$ at $q_1$ and $\widetilde {\mathcal {T}}_0$ at $q_2$ . Then, for any $p\in \gamma $ , as $\widetilde {G}_1|_{\widetilde {\mathcal {M}}_1}=\widetilde {\mathcal {G}}|_{\widetilde {\mathcal {M}}_1}$ ,

$$ \begin{align*}L_{\widetilde{\mathcal{G}}}(q)=\ell_{\widetilde{G}_1}(q)+\text{length}_{\widetilde{\mathcal{G}}}(\gamma_{[q_1,q_2]}).\end{align*} $$

By Lemma 6.9, we know $\ell _{\widetilde {G}_1}(q)\leq K\mathcal {D}_{\widetilde {\mathcal {G}}_1}(q,\widetilde {T}_0)+k$ and we have $\mathcal {D}_{\widetilde {G}_1}(q,\widetilde {\mathcal {T}}_0)<\mathcal {D}_{\widetilde {\mathcal {G}}}(q,\widetilde {T}_0)$ . By the definition of $\epsilon _3$ , $\text {length}_{\widetilde {\mathcal {G}}}(\gamma _{[q_1,q_2]})\leq \epsilon _3$ . Hence, we conclude

(6.15) $$ \begin{align} L_{\widetilde{\mathcal{G}}}(q)&=\ell_{\widetilde{G}_1}(q)+\text{length}_{\widetilde{\mathcal{G}}}(\gamma_{[q_1,q_2]})\nonumber\\ & \leq \ell_{\widetilde{G}_1}(q)+\epsilon \quad\text{as length}_{\widetilde{\mathcal{G}}}(\gamma_{[q_1,q_2]})\leq \epsilon_3\nonumber\\ & \leq C\mathcal{D}_{\widetilde{G}_1}(q,\widetilde{T}_0)+c+\epsilon_3\quad\text{by Lemma }6.9 \nonumber\\ & \leq C\mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_0)+c+\epsilon_3\quad\text{as }\mathcal{D}_{\widetilde{G}_1}(q,\widetilde{T}_0)\leq \mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_0)). \end{align} $$

As all the constants $C,c$ , and $\epsilon $ are independent of the flow line, we conclude that, for all q in $\gamma $ such that $\gamma $ intersects $\widetilde {\mathcal {T}}_q\setminus N^{\prime }_{\delta }(\widetilde {\mathcal {C}}_1\cup \widetilde { \mathcal {C}}_2)$ ,

$$ \begin{align*}L_{\widetilde{\mathcal{G}}}(q)\leq C_1\mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_q)+c_1,\end{align*} $$

where $C_1=C$ and $c_1=d+\epsilon _3$ as defined above.

Remark 6.12. Lemma 6.9 says that every flow line which intersects the boundary components of $\widetilde {M}_1$ outside the ‘bad region’ goes away from the boundary component at a uniformly efficient rate as $t\to \infty $ .

All other hyperbolic plugs, irrespective of ‘attracting’ or ‘repelling’, have the same type of property that if a flow ray intersects a boundary component outside the ‘bad region’, it goes ‘away’ at a uniformly efficient rate from the boundary component when $t\to \infty $ (in the case of attracting plugs) or $t\to -\infty $ (in the case of repelling plugs). Moreover, by taking the maximum over all the constants, we can fix global additive and multiplicative constants which work for all of the hyperbolic plugs.

We conclude this section with two remarks on the separating tori at the boundaries of the hyperbolic plugs, these tori play an important role in this article.

Remark 6.13.

1. (1) As remarked before, the boundary tori are incompressible, that is, they are two-sided and injectively included in the fundamental group $\pi _1(\mathcal {N})$ .

2. (2) If $\widetilde {\mathcal {T}}$ is a component of the lift of some $\partial \widetilde {\mathcal {M}}_i$ , then by [KL98, Theorem 1.1], see also [Ngu19. §4.1], the following happens: $\widetilde {\mathcal {T}}$ is quasi-isometrically embedded in the universal cover $\widetilde {\mathcal {N}}$ . We make it more precise as follows. Consider the lift of a separating torus, say $\widetilde {T}$ . By restricting the Riemannian metric on $\widetilde {\mathcal {T}}$ , we can consider the path metric on $\widetilde {\mathcal {T}}$ induced by the restriction, we call it $d_{\widetilde {\mathcal {T}}}$ . Then, there exists $k_0, k_1$ such that the inclusion map $i:(\widetilde {\mathcal {T}},d_{\widetilde {\mathcal {T}}})\rightarrow (\widetilde {\mathcal {N}},d_{\widetilde {\mathcal {G}}})$ is a $(k_0,k_1)$ -quasi-isometric embedding. We can choose $k_0, k_1$ so that it works for any such $\widetilde {\mathcal {T}}$ .

6.2 Quasigeodesic behavior in the whole manifold

Now we are ready to prove the main theorem, that is, the flow lines of $\widetilde {\Psi }_t$ are uniform quasigeodesics in $\widetilde {\mathcal {N}}$ with respect to $d_{\widetilde {\mathcal {G}}}$ , the path metric induced by $\widetilde {\mathcal {G}}$ . As before, we assume that $\mathcal {N}$ is made of the collection of hyperbolic plugs $\{\mathcal {M}_1,\mathcal {M}_2,\ldots ,\mathcal {M}_n\}$ . Each $\widetilde {\mathcal {M}}_i$ is a manifold with boundary such that $\partial \widetilde {\mathcal {M}}_i$ is a collection of separating planes homeomorphic to $\mathbb {R}^2$ and properly embedded into  $\widetilde {\mathcal {N}}$ .

We first prove that if a flow line or flow ray is fully contained in the universal lift of a single plug $\mathcal {M}_i$ , then it is a quasigeodesic.

Lemma 6.14. There exists $a_3>1$ and $a_4>0$ such that if $\gamma $ is a flow ray or flow line fully contained in a single hyperbolic plug $\widetilde {\mathcal {M}}_i$ , then it is an $(a_3,a_4)$ -quasigeodesic with respect to the metric $d_{\widetilde {\mathcal {G}}}$ .

Proof. As before, without loss of generality, we prove the result only on $\widetilde {\mathcal {M}}_1$ .

In Lemma 5.8, we have proved that the flow lines or flow rays are quasigeodesic with respect to $d_{\widetilde {\mathcal {G}}_1}$ , the path metric of the restriction of $\widetilde {\mathcal {G}}$ on $\widetilde {\mathcal {M}}_1$ . In this lemma, we need to extend the result on the whole manifold $\widetilde {\mathcal {N}}$ with respect to $d_{\widetilde {\mathcal {G}}}$ .

Consider two points $p_1$ and $p_2$ on a flow ray or flow line $\gamma \subset \widetilde {\mathcal {M}}_1$ . Suppose $\sigma :[0,1]\rightarrow ~\widetilde {\mathcal {N}}$ is a minimal path with respect to $\widetilde {\mathcal {G}}$ in $\widetilde {\mathcal {N}}$ connecting $p_1$ and $p_2$ . In other words, length $(\sigma ) = d_{\widetilde {\mathcal {G}}}(p_1,p_2)$ . We argue that the length of $\sigma $ can be approximated by a curve fully contained in $\widetilde {\mathcal {M}}_1$ , without too much increase in length. Suppose $\sigma $ exits $\widetilde {\mathcal {M}}_1$ through a boundary component $\widetilde {\mathcal {T}}$ at $0<v_1<1$ , that is, $\sigma (v_1)\in \widetilde {\mathcal {T}}$ . As $\widetilde {\mathcal {T}}$ is a separating plane in $\widetilde {\mathcal {N}}$ , $\sigma $ must re-enter $\widetilde {\mathcal {M}}_1$ at some first $v_2$ with $0<v_1<v_2<1$ .

By Remark 6.13, $\widetilde {\mathcal {T}}$ is $(k_0,k_1)$ -quasi-isometrically embedded in $\widetilde {\mathcal {N}}$ , and hence we can find a path $\bar {\sigma }:[v_1,v_2]\rightarrow \widetilde {\mathcal {T}}$ such that

$$ \begin{align*}\frac{1}{k_0}\text{length}_{\widetilde{\mathcal{G}}}(\bar{\sigma}_{[v_1,v_2]})-k_1\leq \text{length}_{\widetilde{\mathcal{G}}}(\sigma|_{[v_1,v_2]})\leq k_0\ \text{length}_{\widetilde{\mathcal{G}}}(\bar{\sigma}_{[v_1,v_2]})+k_1.\end{align*} $$

In the definition of $\sigma $ , we can replace $\sigma |_{[v_1,v_2]}$ with $\bar {\sigma }|_{[v_1,v_2]}$ . Now fix $a_6> 0, a_6 << 1$ so that any segment in the image of $\sigma $ with endpoints in $\partial \widetilde {\mathcal {M}}_1$ and interior outside $\widetilde {\mathcal {M}}_1$ , and length $< a_6$ can be pushed into $\partial \widetilde {\mathcal {M}}_1$ to a segment of length at most $2 a_6$ . On $[0,1]$ , there can exist only finitely many closed intervals on which $\sigma $ goes out of $\widetilde {\mathcal {M}}_1$ and with length $> a_6$ . Also replace all of these intervals with minimal curve on respective boundary components as described before, using the quasi-isometry constants $k_0, k_1$ . Choosing ${k_0> 2}$ , then we get a curve $\sigma ':[0,1]\rightarrow \widetilde {\mathcal {M}}_1\subset \widetilde {\mathcal {N}}$ with the same endpoints as $\sigma $ , and such that

$$ \begin{align*}\frac{1}{k_0}\text{length}_{\widetilde{\mathcal{G}}}(\sigma')-k_1\leq \text{length}_{\widetilde{\mathcal{G}}}(\sigma)\leq k_0\ \text{length}_{\widetilde{\mathcal{G}}}(\sigma')+k_1.\end{align*} $$

Note that $\widetilde {\mathcal {G}}_1=\widetilde {\mathcal {G}}|_{\widetilde {\mathcal {M}}_1}$ . In particular, as $\sigma '$ is a path contained in $\widetilde {\mathcal {M}}_1$ and connecting $p_1$ and $p_2$ , then

$$ \begin{align*}d_{\widetilde{\mathcal{G}}_1}(p_1,p_2)\leq\text{length}_{\widetilde{\mathcal{G}}_1}(\sigma')=\text{length}_{\widetilde{\mathcal{G}}}(\sigma').\end{align*} $$

Hence, combining Lemma 5.8 and the above inequality,

$$ \begin{align*} \begin{aligned} \text{length}_{\widetilde{\mathcal{G}}_1}(\gamma_{[p_1,p_2]})&\leq \epsilon d_{\widetilde{\mathcal{G}}_1}(p_1,p_2)+\epsilon'\\ & \leq \epsilon\text{length}_{\widetilde{\mathcal{G}}_1}(\sigma')+\epsilon'\\ & = \epsilon\text{length}_{\widetilde{\mathcal{G}}}(\sigma')+\epsilon'\\ & \leq \epsilon[k_0 \text{length}_{\widetilde{\mathcal{G}}}(\sigma)+ k_0 k_1]+\epsilon'\\ & = \epsilon k_0 d_{\widetilde{\mathcal{G}}}(p_1,p_2)+\epsilon k_0k_1+\epsilon'. \end{aligned} \end{align*} $$

As $\widetilde {\mathcal {G}}_1=\widetilde {\mathcal {G}}|_{\widetilde {\mathcal {M}}_1}$ , $\text {length}_{\widetilde {\mathcal {G}}_1}\gamma _{[p_1,p_2]}=\text {length}_{\widetilde {\mathcal {G}}_1}\gamma _{[p_1,p_2]}$ ; by renaming $a_3=\epsilon k_0$ and ${a_4=\epsilon k_0 k_1+\epsilon '}$ , we conclude the proof of the lemma.

The following is the main result of this article.

Theorem 6.15. There exists $C_0>1$ and $c_0>0$ such that each flow line of $\widetilde {\Psi }_t$ in $\widetilde {\mathcal {N}}$ is a $(C_0,c_0)$ -quasigeodesic with respect to the metric $\widetilde {\mathcal {G}}$ .

Proof. There exists exactly two types of flow lines $\gamma $ of $\widetilde {\Phi }_t$ in $\widetilde {\mathcal {N}}$ :

1. (1) either $\gamma $ is contained in one of $\widetilde {\mathcal {M}}_i$ . In this case, $\gamma $ is contained in the attractor (or repeller) inside $\widetilde {\mathcal {M}}_i$ ;

2. (2) or $\gamma $ intersects the boundary of one of $\widetilde {\mathcal {M}}_i$ . As every boundary component is shared by exactly two plugs, $\gamma $ intersects two adjacent plugs, say $\widetilde {\mathcal {M}}_i$ and $\widetilde {\mathcal {M}}_j$ . In this case, $\gamma $ is subdivided in two rays and each of $\widetilde {\mathcal {M}}_i$ and $\widetilde {\mathcal {M}}_j$ contains exactly one subray, say $\gamma ^+$ and $\gamma ^-$ .

By Lemma 6.14, we know that each flow line which is entirely contained in one of $\widetilde {\mathcal {M}}_i$ is uniform quasigeodesic, that is, all of the first type of flow lines in the above list are $(a_3,a_4)$ -quasigeodesics.

If $\gamma $ intersects a common boundary component of $\widetilde {\mathcal {M}}_i$ and $\widetilde {\mathcal {M}}_j$ , Lemma 6.14 says that both of the forward subray $\gamma ^+$ and the backward subray $\gamma ^-$ are quasigeodesics. However, concatenation of two quasigeodesics is not necessarily a geodesic and that is the main obstacle in this proof. Next, we show that, in our case, concatenation of two quasigeodesic flow rays is a quasigeodesic and the key ingredient of the proof is Lemma 6.11.

Lemma 6.16. Every flow line which intersects a boundary component of a hyperbolic plug is a quasigeodesic.

Proof. Up to reindexing the $\widetilde {\mathcal {M}}_i$ , we can assume that there are lifts $\widetilde {\mathcal {M}}_1, \widetilde {\mathcal {M}}_2$ of $\mathcal {M}_1, \mathcal {M}_2$ , respectively, so that $\gamma $ intersects $\partial \widetilde {\mathcal {M}}_1$ at the boundary component $\widetilde {\mathcal {T}}_0$ and suppose $\widetilde {\mathcal {T}}_0$ is a common boundary component of $\widetilde {\mathcal {M}}_1$ and $\widetilde {\mathcal {M}}_2$ . We can assume that $\widetilde {\mathcal {M}}_1$ is an attracting plug, so it contains the forward ray $\gamma ^+$ and $\widetilde {\mathcal {M}}_2$ must be a repelling plug and contains the backward flow ray $\gamma ^-$ .

Claim 6.17. At least one of $\gamma ^+$ or $\gamma ^-$ intersects $\widetilde {\mathcal {T}}_0$ outside the ‘bad region’. More precisely, at least one of the following is true:

• • for all $q\in \gamma ^+\subset \widetilde {\mathcal {M}}_1$ ,

  $$ \begin{align*}L_{\widetilde{\mathcal{G}}}(q)\leq C_1\mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_0)+c_1;\end{align*} $$

• • or, $\gamma ^-$ satisfies the same property, that is, for all $q\in \gamma ^-\subset \widetilde {\mathcal {M}}_2$ ,

  $$ \begin{align*}L_{\widetilde{\mathcal{G}}}(q)\leq C_1\mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_0)+c_1.\end{align*} $$

It is possible that both of the flow rays $\gamma ^+$ and $\gamma ^-$ satisfy the property.

Proof. We can view $\widetilde {\mathcal {T}}_0$ as a boundary component of $\widetilde {\mathcal {M}}_1$ , and we denote it by $\mathcal {T}_{\widetilde {\mathcal {M}}_1}$ to emphasize this. In the same way, we can view $\widetilde {\mathcal {T}}_0$ as a boundary component of $\widetilde {\mathcal {M}}_2$ , which we denote by $\mathcal {T}_{\widetilde {\mathcal {M}}_2}$ . These boundary components are attached to each other by a map $\widetilde {\Omega }:\widetilde {\mathcal {T}}_{\widetilde {\mathcal {M}}_1}\rightarrow \widetilde {\mathcal {T}}_{\widetilde {\mathcal {M}}_2}$ .

Consider the neighborhood $N^{\prime }_{\delta }(\widetilde {\mathcal {C}}_1\cup \widetilde {\mathcal {C}}_2)$ on $\widetilde {\mathcal {T}}_{\widetilde {\mathcal {M}}_1}$ as described in Lemma 6.11, let us rename it $\mathfrak {N}_{\delta }$ , this is the ‘bad region’ on $\widetilde {\mathcal {T}}_{\widetilde {\mathcal {M}}_1}$ . Similarly, there is another bad region, say $\mathfrak {N}_{\delta '}$ on $\widetilde {\mathcal {T}}_{\widetilde {\mathcal {M}}_2}$ .

Note that we can choose $\delta $ (and $\delta '$ ) in Proposition 6.3 small enough, so that $\widetilde {\Omega }(\mathfrak {N}_{\delta })\cap \mathfrak {N}_{\delta '}=\emptyset $ . In other words, every flow line $\gamma $ which intersects $\widetilde {\mathcal {T}}_0=\widetilde {\mathcal {T}}_{\widetilde {\mathcal {M}}_1}\sqcup \widetilde {\mathcal {T}}_{\widetilde {\mathcal {M}}_2}/\sim $ intersects at least one of the regions $\widetilde {\mathcal {T}}_{\widetilde {\mathcal {M}}_1}\setminus \mathfrak {N}_{\delta }$ or $\widetilde {\mathcal {T}}_{\widetilde {\mathcal {M}}_2}\setminus \mathfrak {N}_{\delta '}$ . If $\gamma $ intersects $\widetilde {\mathcal {T}}_{\widetilde {\mathcal {M}}_1}\setminus \mathfrak {N}_{\delta }$ , then the subray $\gamma ^+$ satisfies the claim by Lemma 6.11, and similarly if $\gamma $ intersects $\widetilde {\mathcal {T}}_{\widetilde {\mathcal {M}}_2}\setminus \mathfrak {N}_{\delta '}$ , the subray $\gamma ^-$ satisfies a similar property.

Continuation of the proof of Lemma 6.16. As before, let $\gamma ^+\subset \widetilde {\mathcal {M}}_1$ and $\gamma ^-\subset \widetilde {\mathcal {M}}_2$ . We assume, without loss of generality, that $\gamma ^+\subset \widetilde {\mathcal {M}}_1$ satisfies Claim 6.17.

Take two points $q,q'\in \gamma $ . As each of the subrays of $\gamma ^+$ and $\gamma ^-$ are uniform quasigeodesics by Lemma 6.14, we can conclude that the flow segment joining q and $q'$ is a quasigeodesic if either $q,q'\in \gamma ^+$ or $\bar {q},q'\in \gamma ^-$ . Hence, we assume $q\in \gamma ^+$ and $q'\in \gamma ^-$ .

As $\widetilde {\mathcal {T}}_0$ is a separating plane on $\widetilde {\mathcal {N}}$ , $\gamma $ must intersect $\widetilde {\mathcal {T}}_0$ . We can conclude that for fixed $q' \in \gamma ^-$ ,

$$ \begin{align*}\mathcal{D}_{\widehat{\mathcal{G}}}(q,\widehat{\mathcal{T}}_0)<d_{\widehat{\mathcal{G}}}(q,q')\quad\text{for all }q\in\gamma^+.\end{align*} $$

Let $\gamma $ intersect $\widetilde {\mathcal {T}}_0$ at $q_1$ . Now fix $q \in \gamma ^+$ . We break the flow segment $\gamma _{[q,q']}$ as $\gamma _{[q,q']}=\gamma _{[q,q_1]}*\gamma _{[q_1,q']}$ . There are two possible cases.

Case I: Suppose $\text {length}_{\widetilde {\mathcal {G}}}(\gamma _{[q,q_1]})\kern1pt{\geq}\kern1pt \text {length}_{\widetilde {\mathcal {G}}}(\gamma _{[q_1,q']})$ . Note that $L_{\widetilde {\mathcal {G}}}(q)\kern1.2pt{=}\kern1.2pt\text {length}_{\widetilde {\mathcal {G}}}(\gamma _{[q,q_1]})$ . By our assumption,

$$ \begin{align*}\text{length}_{\widetilde{\mathcal{G}}}(\gamma_{[q,q']})\leq2\text{length}_{\widetilde{\mathcal{G}}}(\gamma_{[q,q_1]})=2L_{\widetilde{\mathcal{G}}}(q).\end{align*} $$

As we have assumed that $\gamma ^+$ satisfies Claim 6.17,

(6.16) $$ \begin{align} \text{length}_{\widetilde{\mathcal{G}}}(\gamma_{[q,q']})\leq2L_{\widetilde{\mathcal{G}}}(q)\leq 2C_1\mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_0)+2c_1. \end{align} $$

We have observed that $d_{\widetilde {\mathcal {G}}}(q,q')>\mathcal {D}_{\widetilde {\mathcal {G}}}(q,\widetilde {\mathcal {T}}_0)$ as any curve joining q and $q'$ also intersects $\widetilde {\mathcal {T}}_0$ . Hence, replacing in the previous inequality (6.16), we conclude that if $q,q'\in \gamma $ and $\text {length}_{\widetilde {\mathcal {G}}}(\gamma _{[q,q_1]})\geq \text {length}_{\widetilde {\mathcal {G}}}(\gamma _{[q_1,q']})$ , then

(6.17) $$ \begin{align} {\text{length}\gamma_{[q,q']}<2L_{\widetilde{\mathcal{G}}}(q)\leq 2C_1\mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_0)+2c_1\leq 2C_1d_{\widetilde{\mathcal{G}}}(q,q')+2c_1.} \end{align} $$

This finishes the proof of uniform quasigeodesic behavior in this case.

Case II: Now we assume $\text {length}_{\widetilde {\mathcal {G}}}(\gamma _{[q,q_1]})< \text {length}_{\widetilde {\mathcal {G}}}(\gamma _{[q_1,q']})$ .

We first break $\gamma _{[q,q']}$ as $\gamma _{[q,q_1]}*\gamma _{[q_1,q"]}*\gamma _{[q",q']}$ such that $\text {length}_{\widetilde {\mathcal {G}}}(\gamma _{[q,q_1]})= \text {length}_{\widetilde {\mathcal {G}}}(\gamma _{[q_1,q"]})$ as in Figure 4.

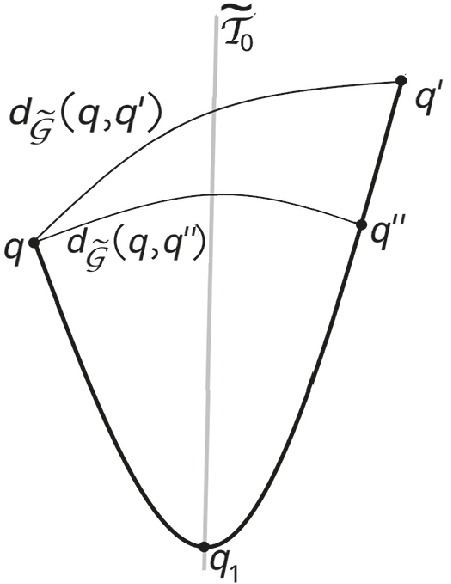
Figure 4 Situation in the universal cover. The curve with arrows in it is the flow line segment from q to $q'$ . The other two curves from q to $q'$ and from q to $q'$ are curves realizing the distance between these pairs of points.

Then by equation (6.17) in Case I, we conclude

(6.18) $$ \begin{align} d_{\widetilde{\mathcal{G}}}(q,q")\leq \text{length}_{\widetilde{\mathcal{G}}}(\gamma_{[q,q"]})\leq 2C_1\mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_0)+2c_1. \end{align} $$

Consider the points $q,q'$ , and $q"$ . The flow segment $\gamma _{[q",q']}$ is an $(a_3,a_4)$ quasigeodesic segment by Lemma 6.14 as it is contained in a single plug $\widetilde {\mathcal {M}}_2$ . Hence,

$$ \begin{align*}\text{length}_{\widetilde{\mathcal{G}}}(\gamma_{[q",q']})\leq a_3 d_{\widetilde{\mathcal{G}}}(q',q")+a_4.\end{align*} $$

By the triangle inequality, we get $d_{\widetilde {\mathcal {G}}}(q',q")\leq d_{\widetilde {\mathcal {G}}}(q',q)+d_{\widetilde {\mathcal {G}}}(q,q")$ . For the flow segment $\gamma _{[q",q']}$ , we conclude

(6.19) $$ \begin{align} \text{length}_{\widetilde{\mathcal{G}}}(\gamma_{[q",q']})&\leq a_3d_{\widetilde{\mathcal{G}}}(q',q")+a_4\nonumber\\ &\leq a_3[d_{\widetilde{\mathcal{G}}}(q',q)+d_{\widetilde{\mathcal{G}}}(q,q")]+a_4\ \ \text{ by the triangle inequality}\nonumber\\ &\leq a_3d_{\widetilde{\mathcal{G}}}(q,q')+a_3[2C_1\mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_0)+2c_1]+a_4 \ \ \text{by (6.18)}\nonumber\\ &= a_3d_{\widetilde{\mathcal{G}}}(q,q')+2a_3C_1\mathcal{D}_{\widetilde{\mathcal{G}}}(q,\mathcal{T})+2a_3c_1+a_4. \end{align} $$

Finally, adding equations (6.18) and (6.19), we conclude

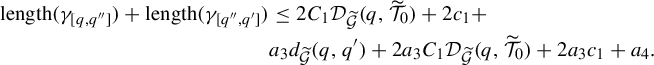(6.20) $$ \begin{align} \text{length}(\gamma_{[q,q"]})+\text{length}(\gamma_{[q",q']})&\leq 2 C_1 \mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_0)+2c_1+\nonumber\\ &a_3d_{\widetilde{\mathcal{G}}}(q,q')+2a_3C_1\mathcal{D}_{\widetilde{\mathcal{G}}}(q,\widetilde{\mathcal{T}}_0)+2a_3c_1+a_4. \end{align} $$

As every path connecting q and $q'$ intersects $\widetilde {\mathcal {T}}_0$ , we get $\mathcal {D}_{\widetilde {\mathcal {G}}}(q,\widetilde {\mathcal {T}}_0)\leq d_{\widetilde {\mathcal {G}}}(q,q')$ . Replacing in the previous equation, we conclude

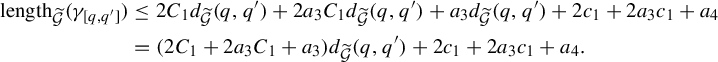(6.21) $$ \begin{align} \text{length}_{\widetilde{\mathcal{G}}}(\gamma_{[q,q']})&\leq 2C_1d_{\widetilde{\mathcal{G}}}(q,q')+ 2a_3C_1d_{\widetilde{\mathcal{G}}}(q,q')+a_3 d_{\widetilde{\mathcal{G}}}(q,q')+2c_1+2a_3c_1 +a_4\nonumber\\ &=(2C_1+2a_3C_1+a_3)d_{\widetilde{\mathcal{G}}}(q,q')+2c_1+2a_3c_1+a_4. \end{align} $$

We rename $C_0=2C_1+2a_3C_1+a_3$ and $c_0=2c_1+2a_3c_1+a_4$ , and equations (6.17) and (6.21) together imply that for any two points q and $q'$ on $\gamma $ ,

$$ \begin{align*}\text{length}_{\widetilde{\mathcal{G}}}{\gamma_{[q,q']}}\leq C_0d_{\widetilde{\mathcal{G}}}(q,q')+c_0.\end{align*} $$

As $\gamma $ was chosen arbitrarily, this completes the proof that any flow line which intersects the common boundary component $\widetilde {\mathcal {T}}_0$ between $\widetilde {\mathcal {M}}_1$ and $\widetilde {\mathcal {M}}_2$ is a quasigeodesic. Moreover, the same multiplicative and additive constants work for all flow lines intersecting $\widetilde {\mathcal {T}}_0$ .

In the beginning of the proof, we fixed $\widetilde {\mathcal {M}}_1$ and $\widetilde {\mathcal {M}}_2$ and their common boundary component $\widetilde {\mathcal {T}}_0$ , but the same method works for all other plugs which intersect along boundaries. The quasigeodesic constants differ for different choices of boundary components. Finally, as there are only finitely many plugs in $\mathcal {N}$ , we can take maximums over all possibilities of boundary components in $\widetilde {\mathcal {N}}$ and we can choose global quasigeodesic constants for the flow lines which intersect any of the boundary components.

This ends the proof of Lemma 6.16.

Lemmas 6.14 and 6.16 together imply that any flow lines of $\widetilde {\Psi }_t$ in $\widetilde {\mathcal {N}}$ are uniformly quasigeodesic.

This completes the proof of Theorem 6.15.

Remark 6.18. In the proof of the final theorem in §5.2, we used two key ideas:

1. (1) every flow ray of a flow line contained in a single plug is quasigeodesic;

2. (2) every flow ray which intersects a boundary component outside a narrow region eventually goes away uniformly efficiently from the boundary component it intersects.

This suggests that the same general techniques used in this proof can be applied to study quasigeodesic behavior of flows in different contexts where these two properties hold.

7 Comments on the Franks–Williams manifolds $\mathcal {N}$ and a question

As before, we consider the decomposition of $\mathcal {N}$ as the union

$$ \begin{align*}\mathcal{N}=\mathcal{M}_1\cup \mathcal{M}_2 \cup \cdots \cup \mathcal{M}_n,\end{align*} $$

where the components $\mathcal {M}_i$ intersect each other along their boundaries and the boundary components of $\mathcal {M}_i$ are homeomorphic to tori. We denote the collection of boundary components as $\{\mathcal {T}_j|j\in J\}$ , where each $\mathcal {T}_j$ is a common boundary of two plugs from the collection $\mathcal {M}_1, \mathcal {M}_2,\ldots ,\mathcal {M}_n$ . Now, we again emphasize some properties of the manifold $\mathcal {N}$ and the collection of torus $\{\mathcal {T}_j|j\in J\}$ .

1. (1) $\mathcal {N}$ is irreducible: as $\mathcal {N}$ supports an Anosov flow, it supports a taut foliation (take the weak-stable or the weak-unstable foliation). Then, by Novikov’s theorem, $\mathcal {N}$ is an irreducible manifold.

2. (2) JSJ-decomposition of $\mathcal {N}$ : every irreducible orientable 3-manifold supports a JSJ-decomposition, that is, a collection of tori separating the manifold into atoroidal and/or Seifert fibered pieces. In our case, we can show that the collection $\{\mathcal {T}_j|j\in J\}$ is a minimal JSJ-decomposition on $\mathcal {N}$ . The orientability condition can be satisfied by moving to a finite cover of $\mathcal {N}$ (if required). It is easy to check from the construction of the plugs that each torus $\mathcal {T}_j$ is incompressible, that is, closed, 2-sided, and canonically injects in the fundamental group of $\mathcal {N}$ . To see that the collection $\{\mathcal {T}_j|j\in J\}$ is minimal, we claim that each piece in the decomposition with respect to $\{\mathcal {T}_j|j\in J\}$ is atoroidal, see detail in item $3$ below.

3. (3) $\mathcal {N}$ is non-hyperbolic and non-Seifert fibered: as there exists incompressible tori $\mathcal {T}_j$ in $\mathcal {N}$ , it follows that $\mathcal {N}$ cannot be a hyperbolic manifold. To see that $\mathcal {M}$ is also non-Seifert fibered, we consider the plugs $\mathcal {M}_1,\mathcal {M}_2,\ldots ,\mathcal {M}_n$ which are also the components of the torus decomposition, and we note that each of the plugs are constructed by removing solid torus neighborhoods from mapping tori of hyperbolic maps on $\mathbb {T}^2$ , that is, $\mathbb {T}^2\times [0,1]/((x,1)\sim (\Phi (x),0))$ for some ${\Phi :\mathbb {T}^2\to \mathbb {T}^2}$ homotopic to a hyperbolic map on $\mathbb {T}^2$ . They are mapping tori of pseudo-Anosov homeomorphisms of a torus minus finitely many disks. Additionally, it is well known that such mapping tori are atoroidal, and hence non-Seifert fibered. This now implies that these are the pieces of the JSJ decomposition of $\mathcal {N}$ , and all pieces are atoroidal.

4. (4) Existence of a non-positively curved metric on $\mathcal {N}$ : as the manifold $\mathcal {N}$ is $Haken$ , that is, it is irreducible, contains a closed incompressible surface, and it has one atoroidal piece, we can define a non-positively curved Riemannian metric on $\mathcal {M}$ by [Lee95, Theorem 3.3]. This opens a potentially new direction to explore as described below.

7.1 Future questions

By item (4) above, we can define a non-positively curved Riemannian metric on $\mathcal {N}$ . Then the universal cover $\widetilde {\mathcal {N}}$ with the path metric induced by the non-positively curved Riemannian metric is $\mathrm {CAT}(0)$ . For a $\mathrm {CAT}(0)$ -space, we can define different types of ‘boundaries at infinity’, for example, the Tits boundary or the Morse boundary and we can define topologies on the boundary at infinity, $\partial _{\infty }\widetilde {\mathcal {N}}$ . For example, one question to ask is whether the weak-stable or weak-unstable foliations of $\Psi _t$ satisfy the continuous extension property.

Question 7.1. Suppose $F\in \widetilde {\mathcal {F}}^{ws}$ or $\widetilde {\mathcal {F}}^{wu}$ of $\widetilde {\Psi }_t$ . It is known that leaves of the weak-stable or weak-stable foliations of Anosov flows are Gromov hyperbolic and we can define the Gromov boundary $S^1(F)$ (it is a circle). Then, does the inclusion $i:F\rightarrow \widetilde {\mathcal {N}}$ extend continuously to a map $\hat {i}:F\cup S^1(F)\rightarrow \widetilde {\mathcal {N}}\cup \partial _{\infty }\widetilde {\mathcal {N}}$ ?

Similar types of questions have been extensively studied for Anosov flows on hyperbolic $3$ -manifolds. A big difference in the case of Franks–Williams manifolds is that the Morse lemma is not true in general, but in some particular cases, there is a possibility that the quasigeodesic flow rays are boundedly away from actual geodesic rays. Hence, this question is relevant for quasigeodesic Anosov flow on non-positively curved manifolds.