Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-12T08:42:26.430Z Has data issue: false hasContentIssue false
  • English
  • Français

Nilpotent dynamics in dimension one: structure and smoothness

Published online by Cambridge University Press:  15 June 2015

KIRAN PARKHE
KIRAN PARKHE*
Affiliation:
Faculty of Mathematics, Technion – Israel Institute of Technology, Technion City, Haifa 32000, Israel email parkhe@tx.technion.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

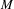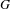Let $M$ be a connected $1$-manifold, and let $G$ be a finitely-generated nilpotent group of homeomorphisms of 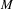$M$. Our main result is that one can find a collection 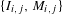$\{I_{i,j},M_{i,j}\}$ of open disjoint intervals with dense union in 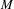$M$, such that the intervals are permuted by the action of 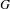$G$, and the restriction of the action to any 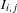$I_{i,j}$ is trivial, while the restriction of the action to any $M_{i,j}$ is minimal and abelian. It is a classical result that if 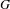$G$ is a finitely-generated, torsion-free nilpotent group, then there exist faithful continuous actions of 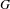$G$ on 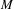$M$. Farb and Franks [Groups of homeomorphisms of one-manifolds, III: Nilpotent subgroups. Ergod. Th. & Dynam. Sys.23 (2003), 1467–1484] showed that for such 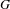$G$, there always exists a faithful 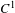$C^{1}$ action on 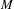$M$. As an application of our main result, we show that every continuous action of 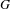$G$ on 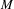$M$ can be conjugated to a 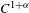$C^{1+\unicode[STIX]{x1D6FC}}$ action for any 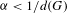$\unicode[STIX]{x1D6FC}<1/d(G)$, where 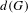$d(G)$ is the degree of polynomial growth of 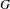$G$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 7 , October 2016 , pp. 2258 - 2272
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bass, H.. The degree of polynomial growth of finitely generated nilpotent groups. Proc. Lond. Math. Soc. 25(3) (1972), 603–614.CrossRefGoogle Scholar
Bonatti, C., Monteverde, I., Navas, A. and Rivas, C.. Rigidity for $C^{1}$ actions on the interval arising from hyperbolicity I: Solvable groups. Preprint, 2013, http://arxiv.org/abs/1309.5277.Google Scholar
Cantwell, J. and Conlon, L.. An interesting class of C 1 foliations. Topology Appl. 126 (2002), 281–297.Google Scholar
Castro, G., Jorquera, E. and Navas, A.. Sharp regularity for certain nilpotent group actions on the interval. Math. Ann. (2011), 1–52.Google Scholar
de la Harpe, P.. Topics in Geometric Group Theory. University of Chicago Press, Chicago, 2000.Google Scholar
Denjoy, A.. Sur les courbes définies par les équations différentielles à la surface du tore. J. Math. Pures Appl. 11 (1932), 333–376.Google Scholar
Deroin, B., Kleptsyn, V. and Navas, A.. Sur la dynamique unidimensionnelle en régularité intermédiaire. Acta Math. 199 (2007), 199–262.CrossRefGoogle Scholar
Farb, B. and Franks, J.. Groups of homeomorphisms of one-manifolds, III: Nilpotent subgroups. Ergod. Th. & Dynam. Sys. 23 (2003), 1467–1484.CrossRefGoogle Scholar
Ghys, É.. Groups acting on the circle. Enseign. Math. 47(3/4) (2001), 329–408.Google Scholar
Grigorchuk, R. and Maki, A.. On a group of intermediate growth that acts on a line by homeomorphisms. Math. Notes 53 (1993), 146–157.Google Scholar
Gromov, M.. Geometric Group Theory. Vol. 2, Asymptotic Invariants of Infinite Groups (Lecture Note Series, London Mathematical Sciences, 182) . Eds. Niblo, G. and Roller, M.. Cambridge University Press, Cambridge, 1993.Google Scholar
Gromov, M.. Groups of polynomial growth and expanding maps. Publ. Math. Inst. Hautes Études Sci. 53(1) (1981), 53–78.CrossRefGoogle Scholar
Guelman, N. and Liousse, I.. C 1 -actions of Baumslag-Solitar groups on S 1 . Algebr. Geom. Topol. 11(3) (2011), 1701–1707.CrossRefGoogle Scholar
Guivarc’h, Y.. Groupes de Lie à croissance polynomiale. C. R. Acad. Sci. Paris Sér. A 272 (1971), 1695–1696.Google Scholar
Harrison, J.. Unsmoothable diffeomorphisms on higher dimensional manifolds. Proc. Amer. Math. Soc. 73(2) (1979), 249–255.CrossRefGoogle Scholar
Jorquera, E.. Sobre los grupos de difeomorfismos del intervalo y del círculo. PhD Thesis, University of Chile, 2009.Google Scholar
Malcev, A.. On a class of homogeneous spaces. Amer. Math. Soc. Transl. 39 (1951).Google Scholar
Navas, A.. Groups of Circle Diffeomorphisms. University of Chicago Press, Chicago, 2011.Google Scholar
Navas, A.. Growth of groups and diffeomorphisms of the interval. Geom. Funct. Anal. 18(3) (2008), 988–1028.CrossRefGoogle Scholar
Navas, A.. On centralizers of interval diffeomorphisms in critical (intermediate) regularity. J. Anal. Math. 121(1) (2013), 1–30.Google Scholar
Navas, A.. Sur les rapprochements par conjugaison en dimension 1 et classe $C^{1}$ . Compos. Math. to appear. Preprint, 2012, http://arxiv.org/abs/1208.4815.Google Scholar
Osin, D.. Subgroup distortions in nilpotent groups. Comm. Algebra 29(12) (2001), 5439–5463.Google Scholar
Plante, J.. Foliations with measure preserving holonomy. Annals of Math. 102 (1975), 327–361.Google Scholar
Plante, J. and Thurston, W.. Polynomial growth in holonomy groups of foliations. Comment. Math. Helv. 51 (1976), 567–584.Google Scholar
Raghunathan, M.. Discrete Subgroups of Lie Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, 68) . Springer, Berlin, 1972.CrossRefGoogle Scholar
Robinson, D. J. S.. A Course in the Theory of Groups (Graduate Texts in Mathematics, 80) . Springer, New York, 1996.CrossRefGoogle Scholar
Witte, D.. Arithmetic groups of higher ℚ-rank cannot act on 1-manifolds. Proc. Amer. Math. Soc. 122(2) (1994), 333–340.Google Scholar