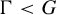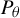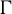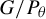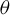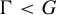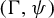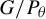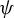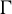1. Introduction
Let G be a connected semisimple real algebraic group and
![]() $\mathfrak g=\operatorname {Lie} G$
. Let A be a maximal real split torus of G and set
$\mathfrak g=\operatorname {Lie} G$
. Let A be a maximal real split torus of G and set
![]() $\mathfrak {a} = \operatorname {Lie} A$
. Fix a positive Weyl chamber
$\mathfrak {a} = \operatorname {Lie} A$
. Fix a positive Weyl chamber
![]() $\mathfrak a^+<\mathfrak a$
and a maximal compact subgroup
$\mathfrak a^+<\mathfrak a$
and a maximal compact subgroup
![]() $K< G$
such that the Cartan decomposition
$K< G$
such that the Cartan decomposition
![]() $G=K (\exp \mathfrak a^+) K$
holds. We denote by
$G=K (\exp \mathfrak a^+) K$
holds. We denote by
![]() $\mu (g)\in \mathfrak a$
the Cartan projection of
$\mu (g)\in \mathfrak a$
the Cartan projection of
![]() $g\in G$
, that is, the unique element of
$g\in G$
, that is, the unique element of
![]() $\mathfrak a^+$
such that
$\mathfrak a^+$
such that
![]() $g\in K \exp (\mu (g))K$
. Let
$g\in K \exp (\mu (g))K$
. Let
![]() $\Pi $
be the set of all simple roots for
$\Pi $
be the set of all simple roots for
![]() $(\mathfrak g, \mathfrak a^+)$
and fix a non-empty subset
$(\mathfrak g, \mathfrak a^+)$
and fix a non-empty subset
![]() $\theta \subset \Pi $
. Let
$\theta \subset \Pi $
. Let
![]() $P_\theta $
be the standard parabolic subgroup of G corresponding to
$P_\theta $
be the standard parabolic subgroup of G corresponding to
![]() $\theta $
and set
$\theta $
and set
Let
![]() $\Gamma <G$
be a Zariski dense discrete subgroup. Denote by
$\Gamma <G$
be a Zariski dense discrete subgroup. Denote by
![]() $\Lambda _\theta \subset \mathcal F_{\theta }$
the limit set of
$\Lambda _\theta \subset \mathcal F_{\theta }$
the limit set of
![]() $\Gamma $
, which is the unique
$\Gamma $
, which is the unique
![]() $\Gamma $
-minimal subset of
$\Gamma $
-minimal subset of
![]() $\mathcal F_\theta $
[Reference Benoist1]. Let
$\mathcal F_\theta $
[Reference Benoist1]. Let
![]() $\mathfrak {a}_\theta =\bigcap _{\alpha \in \Pi - \theta } \ker \alpha $
. For a linear form
$\mathfrak {a}_\theta =\bigcap _{\alpha \in \Pi - \theta } \ker \alpha $
. For a linear form
![]() $\psi \in \mathfrak a_\theta ^*$
, a Borel probability measure
$\psi \in \mathfrak a_\theta ^*$
, a Borel probability measure
![]() $\nu $
on
$\nu $
on
![]() $\mathcal {F}_\theta $
is called a
$\mathcal {F}_\theta $
is called a
![]() $(\Gamma , \psi )$
-conformal measure if
$(\Gamma , \psi )$
-conformal measure if
where
![]() $\gamma _* \nu (B) = \nu (\gamma ^{-1}B)$
for any Borel subset
$\gamma _* \nu (B) = \nu (\gamma ^{-1}B)$
for any Borel subset
![]() $B\subset \mathcal F_\theta $
and
$B\subset \mathcal F_\theta $
and
![]() $\beta _\xi ^\theta $
denotes the
$\beta _\xi ^\theta $
denotes the
![]() $\mathfrak a_\theta $
-valued Busemann map defined in equation (2.2). By a
$\mathfrak a_\theta $
-valued Busemann map defined in equation (2.2). By a
![]() $\Gamma $
-Patterson–Sullivan measure on
$\Gamma $
-Patterson–Sullivan measure on
![]() $\mathcal F_\theta $
, we mean a
$\mathcal F_\theta $
, we mean a
![]() $(\Gamma ,\psi )$
-conformal measure supported on
$(\Gamma ,\psi )$
-conformal measure supported on
![]() $\Lambda _\theta $
for some
$\Lambda _\theta $
for some
![]() $\psi \in \mathfrak a_{\theta }^*$
.
$\psi \in \mathfrak a_{\theta }^*$
.
Patterson–Sullivan measures play a fundamental role in the study of geometry and dynamics for
![]() $\Gamma $
-actions. For G of rank one, they were constructed by Patterson and Sullivan for any non-elementary discrete subgroup
$\Gamma $
-actions. For G of rank one, they were constructed by Patterson and Sullivan for any non-elementary discrete subgroup
![]() $\Gamma $
of G [Reference Patterson17, Reference Sullivan22], and hence the name. Their construction was generalized by Quint for any Zariski dense subgroup of a semisimple real algebraic group [Reference Quint19].
$\Gamma $
of G [Reference Patterson17, Reference Sullivan22], and hence the name. Their construction was generalized by Quint for any Zariski dense subgroup of a semisimple real algebraic group [Reference Quint19].
A finitely generated subgroup
![]() $\Gamma <G$
is called a
$\Gamma <G$
is called a
![]() $\theta $
-Anosov subgroup if there exist
$\theta $
-Anosov subgroup if there exist
![]() $C_1, C_2>0$
such that for all
$C_1, C_2>0$
such that for all
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $\alpha \in \theta $
,
$\alpha \in \theta $
,
where
![]() $|\gamma |$
denotes the word length of
$|\gamma |$
denotes the word length of
![]() $\gamma $
with respect to a fixed finite generating set of
$\gamma $
with respect to a fixed finite generating set of
![]() $\Gamma $
. A
$\Gamma $
. A
![]() $\theta $
-Anosov subgroup is necessarily a word hyperbolic group [Reference Kapovich, Leeb and Porti11, Theorem 1.5, Corollary 1.6]. The notion of Anosov subgroups was first introduced by Labourie for surface groups [Reference Labourie15], and was extended to general word hyperbolic groups by Guichard and Wienhard [Reference Guichard and Wienhard8]. Several equivalent characterizations have been established, one of which is the above definition (see [Reference Guéritaud, Guichard, Kassel and Wienhard7, Reference Kapovich and Leeb9–Reference Kapovich, Leeb and Porti11]). Anosov subgroups are regarded as natural generalizations of convex cocompact subgroups of rank one groups, and include the images of Hitchin representations and of maximal representations as well as higher rank Schottky subgroups; see [Reference Kassel12, Reference Wienhard23].
$\theta $
-Anosov subgroup is necessarily a word hyperbolic group [Reference Kapovich, Leeb and Porti11, Theorem 1.5, Corollary 1.6]. The notion of Anosov subgroups was first introduced by Labourie for surface groups [Reference Labourie15], and was extended to general word hyperbolic groups by Guichard and Wienhard [Reference Guichard and Wienhard8]. Several equivalent characterizations have been established, one of which is the above definition (see [Reference Guéritaud, Guichard, Kassel and Wienhard7, Reference Kapovich and Leeb9–Reference Kapovich, Leeb and Porti11]). Anosov subgroups are regarded as natural generalizations of convex cocompact subgroups of rank one groups, and include the images of Hitchin representations and of maximal representations as well as higher rank Schottky subgroups; see [Reference Kassel12, Reference Wienhard23].
A special case of our main theorem is the following non-concentration property of Patterson–Sullivan measures for
![]() $\theta $
-Anosov subgroups.
$\theta $
-Anosov subgroups.
Theorem 1.1. Let
![]() $\Gamma <G$
be a Zariski dense
$\Gamma <G$
be a Zariski dense
![]() $\theta $
-Anosov subgroup. For any
$\theta $
-Anosov subgroup. For any
![]() $\Gamma $
-Patterson–Sullivan measure
$\Gamma $
-Patterson–Sullivan measure
![]() $\nu $
on
$\nu $
on
![]() $\mathcal F_\theta $
, we have
$\mathcal F_\theta $
, we have
for any proper subvariety S of
![]() $ \mathcal F_\theta $
.
$ \mathcal F_\theta $
.
Remark 1.2. This was proved by Flaminio and Spatzier [Reference Flaminio and Spatzier6] for
![]() $G=\operatorname {SO}(n,1)$
,
$G=\operatorname {SO}(n,1)$
,
![]() $n\ge 2$
, and by Edwards, Lee, and Oh [Reference Edwards, Lee and Oh5] when
$n\ge 2$
, and by Edwards, Lee, and Oh [Reference Edwards, Lee and Oh5] when
![]() $\theta =\Pi $
and the opposition involution of G is trivial in equation (2.1).
$\theta =\Pi $
and the opposition involution of G is trivial in equation (2.1).
Indeed, we work with a more general class of discrete subgroups, called
![]() $\theta $
-transverse subgroups. Denote by
$\theta $
-transverse subgroups. Denote by
![]() $\operatorname {i}$
the opposition involution of G (see equation (2.1)).
$\operatorname {i}$
the opposition involution of G (see equation (2.1)).
Definition 1.3. A discrete subgroup
![]() $\Gamma < G$
is called
$\Gamma < G$
is called
![]() $\theta $
-transverse if:
$\theta $
-transverse if:
-
• it is
 $\theta $
-regular, that is,
$\theta $
-regular, that is,
 $ \liminf _{\gamma \in \Gamma } \alpha (\mu ({\gamma }))=\infty $
for all
$ \liminf _{\gamma \in \Gamma } \alpha (\mu ({\gamma }))=\infty $
for all
 $\alpha \in \theta $
; and
$\alpha \in \theta $
; and -
• it is
 $\theta $
-antipodal, that is, any two distinct
$\theta $
-antipodal, that is, any two distinct
 $\xi , \eta \in \Lambda _{\theta \cup \operatorname {i}(\theta )}$
are in general position.
$\xi , \eta \in \Lambda _{\theta \cup \operatorname {i}(\theta )}$
are in general position.
Since
![]() $\operatorname {i} (\mu ( g))=\mu (g^{-1}) $
for all
$\operatorname {i} (\mu ( g))=\mu (g^{-1}) $
for all
![]() $g\in G$
, it follows that
$g\in G$
, it follows that
![]() $\Gamma $
is
$\Gamma $
is
![]() $\theta $
-transverse if and only if
$\theta $
-transverse if and only if
![]() $\Gamma $
is
$\Gamma $
is
![]() $\operatorname {i}(\theta )$
-transverse. The class of
$\operatorname {i}(\theta )$
-transverse. The class of
![]() $\theta $
-transverse subgroups includes all discrete subgroups of rank one Lie groups,
$\theta $
-transverse subgroups includes all discrete subgroups of rank one Lie groups,
![]() $\theta $
-Anosov subgroups, and relatively
$\theta $
-Anosov subgroups, and relatively
![]() $\theta $
-Anosov subgroups.
$\theta $
-Anosov subgroups.
Let
![]() $p_{\theta } : \mathfrak a \to \mathfrak a_{\theta }$
be the projection which is invariant under all Weyl elements fixing
$p_{\theta } : \mathfrak a \to \mathfrak a_{\theta }$
be the projection which is invariant under all Weyl elements fixing
![]() $\mathfrak a_{\theta }$
pointwise, and set
$\mathfrak a_{\theta }$
pointwise, and set
![]() $\mu _\theta =p_\theta \circ \mu $
. A linear form
$\mu _\theta =p_\theta \circ \mu $
. A linear form
![]() $\psi \in \mathfrak a_{\theta }^*$
is said to be
$\psi \in \mathfrak a_{\theta }^*$
is said to be
![]() $(\Gamma , \theta )$
-proper if the composition
$(\Gamma , \theta )$
-proper if the composition
![]() $\psi \circ \mu _\theta : \Gamma \to [-\varepsilon , \infty )$
is a proper map for some
$\psi \circ \mu _\theta : \Gamma \to [-\varepsilon , \infty )$
is a proper map for some
![]() $\varepsilon> 0$
. The following is our main theorem from which Theorem 1.1 is deduced by applying Selberg’s lemma [Reference Selberg21].
$\varepsilon> 0$
. The following is our main theorem from which Theorem 1.1 is deduced by applying Selberg’s lemma [Reference Selberg21].
Theorem 1.4. Let
![]() $\Gamma <G$
be a Zariski dense virtually torsion-free
$\Gamma <G$
be a Zariski dense virtually torsion-free
![]() $\theta $
-transverse subgroup. Let
$\theta $
-transverse subgroup. Let
![]() $\psi \in \mathfrak a_{\theta }^*$
be a
$\psi \in \mathfrak a_{\theta }^*$
be a
![]() $(\Gamma , \theta )$
-proper linear form such that
$(\Gamma , \theta )$
-proper linear form such that
![]() $\sum _{\gamma \in \Gamma } e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
. For any
$\sum _{\gamma \in \Gamma } e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
. For any
![]() $(\Gamma , \psi )$
-Patterson–Sullivan measure
$(\Gamma , \psi )$
-Patterson–Sullivan measure
![]() $\nu $
on
$\nu $
on
![]() $\mathcal F_{\theta }$
, we have
$\mathcal F_{\theta }$
, we have
for any proper subvariety S of
![]() $ \mathcal F_\theta $
.
$ \mathcal F_\theta $
.
For a
![]() $\theta $
-Anosov
$\theta $
-Anosov
![]() $\Gamma $
, the existence of a
$\Gamma $
, the existence of a
![]() $(\Gamma , \psi )$
-Patterson–Sullivan measure implies that
$(\Gamma , \psi )$
-Patterson–Sullivan measure implies that
![]() $\psi $
is
$\psi $
is
![]() $(\Gamma , \theta )$
-proper and
$(\Gamma , \theta )$
-proper and
![]() $\sum _{\gamma \in \Gamma } e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
[Reference Lee and Oh16, Reference Sambarino20]. Therefore, Theorem 1.1 is a special case of Theorem 1.4.
$\sum _{\gamma \in \Gamma } e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
[Reference Lee and Oh16, Reference Sambarino20]. Therefore, Theorem 1.1 is a special case of Theorem 1.4.
The following is added to the proof. The growth indicator
![]() $\psi _\Gamma ^\theta $
is a higher rank version of the classical critical exponent of
$\psi _\Gamma ^\theta $
is a higher rank version of the classical critical exponent of
![]() $\Gamma $
[Reference Kim, Oh and Wang13, Reference Quint18]. For a Zariski dense
$\Gamma $
[Reference Kim, Oh and Wang13, Reference Quint18]. For a Zariski dense
![]() $\theta $
-transverse subgroup and a
$\theta $
-transverse subgroup and a
![]() $(\Gamma , \theta )$
-proper
$(\Gamma , \theta )$
-proper
![]() $\psi \in \mathfrak a_{\theta }^*$
, the existence of a
$\psi \in \mathfrak a_{\theta }^*$
, the existence of a
![]() $(\Gamma , \psi )$
-conformal measure implies that
$(\Gamma , \psi )$
-conformal measure implies that
![]() $\psi $
is bounded from below by
$\psi $
is bounded from below by
![]() $\psi _\Gamma ^\theta $
([Reference Quint19, Theorem 8.1] for
$\psi _\Gamma ^\theta $
([Reference Quint19, Theorem 8.1] for
![]() $\theta = \Pi $
, [Reference Kim, Oh and Wang13, Theorem 1.4] for a general
$\theta = \Pi $
, [Reference Kim, Oh and Wang13, Theorem 1.4] for a general
![]() $\theta $
). When
$\theta $
). When
![]() $\Gamma $
is relatively
$\Gamma $
is relatively
![]() $\theta $
-Anosov and
$\theta $
-Anosov and
![]() $\psi $
is tangent to
$\psi $
is tangent to
![]() $\psi _\Gamma ^\theta $
, the abscissa of convergence of the series
$\psi _\Gamma ^\theta $
, the abscissa of convergence of the series
![]() $s \mapsto \sum _{\gamma \in \Gamma } e^{-s\psi (\mu _{\theta }(\gamma ))}$
is equal to
$s \mapsto \sum _{\gamma \in \Gamma } e^{-s\psi (\mu _{\theta }(\gamma ))}$
is equal to
![]() $1$
, and a recent work [Reference Canary, Zhang and Zimmer3, Theorem 1.1] shows that
$1$
, and a recent work [Reference Canary, Zhang and Zimmer3, Theorem 1.1] shows that
![]() $\sum _{\gamma \in \Gamma } e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
. Therefore, Theorem 1.4 also applies in this setting.
$\sum _{\gamma \in \Gamma } e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
. Therefore, Theorem 1.4 also applies in this setting.
2. Ergodic properties of Patterson–Sullivan measures
Let G be a connected semisimple real algebraic group. Let
![]() $P < G$
be a minimal parabolic subgroup with a fixed Langlands decomposition
$P < G$
be a minimal parabolic subgroup with a fixed Langlands decomposition
![]() $P=MAN, $
where A is a maximal real split torus of G, M is a maximal compact subgroup commuting with A, and N is the unipotent radical of P. We fix a positive Weyl chamber
$P=MAN, $
where A is a maximal real split torus of G, M is a maximal compact subgroup commuting with A, and N is the unipotent radical of P. We fix a positive Weyl chamber
![]() $\mathfrak {a}^+\subset \mathfrak {a} = \operatorname {Lie}A$
so that
$\mathfrak {a}^+\subset \mathfrak {a} = \operatorname {Lie}A$
so that
![]() $\log N$
consists of positive root subspaces. Recall that
$\log N$
consists of positive root subspaces. Recall that
![]() $K< G$
denotes a maximal compact subgroup such that the Cartan decomposition
$K< G$
denotes a maximal compact subgroup such that the Cartan decomposition
![]() $G=K(\exp \mathfrak a^+) K$
holds and denote by
$G=K(\exp \mathfrak a^+) K$
holds and denote by
![]() $\mu :G\to \mathfrak {a}^+$
the Cartan projection, that is,
$\mu :G\to \mathfrak {a}^+$
the Cartan projection, that is,
![]() $\mu (g) \in \mathfrak {a}^+$
is the unique element such that
$\mu (g) \in \mathfrak {a}^+$
is the unique element such that
![]() $g\in K\exp (\mu (g))K$
for
$g\in K\exp (\mu (g))K$
for
![]() $g\in G$
. Let
$g\in G$
. Let
![]() $w_0\in K$
be an element of the normalizer of A such that
$w_0\in K$
be an element of the normalizer of A such that
![]() $\operatorname {Ad}_{w_0}\mathfrak a^+= -\mathfrak a^+$
. The opposition involution
$\operatorname {Ad}_{w_0}\mathfrak a^+= -\mathfrak a^+$
. The opposition involution
![]() $\operatorname {i}:\mathfrak a \to \mathfrak a$
is defined by
$\operatorname {i}:\mathfrak a \to \mathfrak a$
is defined by
Note that
![]() $\mu (g^{-1})=\operatorname {i} (\mu (g))$
for all
$\mu (g^{-1})=\operatorname {i} (\mu (g))$
for all
![]() $g\in G$
.
$g\in G$
.
Let
![]() $\Pi $
denote the set of all simple roots for
$\Pi $
denote the set of all simple roots for
![]() $(\mathfrak g, \mathfrak a^+)$
. Fix a non-empty subset
$(\mathfrak g, \mathfrak a^+)$
. Fix a non-empty subset
![]() $\theta \subset \Pi $
. Let
$\theta \subset \Pi $
. Let
![]() $ P_\theta ^-$
and
$ P_\theta ^-$
and
![]() $P_\theta ^+$
be a pair of opposite standard parabolic subgroups of G corresponding to
$P_\theta ^+$
be a pair of opposite standard parabolic subgroups of G corresponding to
![]() $\theta $
; here,
$\theta $
; here,
![]() $P_\theta :=P_\theta ^-$
is chosen to contain P. We set
$P_\theta :=P_\theta ^-$
is chosen to contain P. We set
We also write
![]() $\mathcal F_\theta =\mathcal F_\theta ^-$
for simplicity. We set
$\mathcal F_\theta =\mathcal F_\theta ^-$
for simplicity. We set
![]() $P=P_\Pi $
and
$P=P_\Pi $
and
![]() $\mathcal F=\mathcal F_\Pi $
. Since
$\mathcal F=\mathcal F_\Pi $
. Since
![]() $P_\theta ^+$
is conjugate to
$P_\theta ^+$
is conjugate to
![]() $P_{\operatorname {i}(\theta )}$
, we have
$P_{\operatorname {i}(\theta )}$
, we have
![]() $\mathcal F_{\operatorname {i}(\theta )}=\mathcal F_\theta ^+$
. We say
$\mathcal F_{\operatorname {i}(\theta )}=\mathcal F_\theta ^+$
. We say
![]() $\xi \in \mathcal F_\theta $
and
$\xi \in \mathcal F_\theta $
and
![]() $\eta \in \mathcal F_{\operatorname {i}(\theta )}$
are in general position if
$\eta \in \mathcal F_{\operatorname {i}(\theta )}$
are in general position if
![]() $(\xi , \eta )\in G (P_\theta ^-, P_\theta ^+)$
under the diagonal G-action on
$(\xi , \eta )\in G (P_\theta ^-, P_\theta ^+)$
under the diagonal G-action on
![]() $\mathcal F_\theta \times \mathcal F_{\operatorname {i}(\theta )}$
. We write
$\mathcal F_\theta \times \mathcal F_{\operatorname {i}(\theta )}$
. We write
which is the unique open G-orbit in
![]() $\mathcal F_\theta \times \mathcal F_{\operatorname {i}(\theta )}$
.
$\mathcal F_\theta \times \mathcal F_{\operatorname {i}(\theta )}$
.
Let
![]() $\mathfrak {a}_\theta =\bigcap _{\alpha \in \Pi - \theta } \ker \alpha $
and denote by
$\mathfrak {a}_\theta =\bigcap _{\alpha \in \Pi - \theta } \ker \alpha $
and denote by
![]() $\mathfrak a_{\theta }^*$
the space of all linear forms on
$\mathfrak a_{\theta }^*$
the space of all linear forms on
![]() $\mathfrak a_{\theta }$
. We set
$\mathfrak a_{\theta }$
. We set
![]() $p_\theta :\mathfrak {a}\to \mathfrak {a}_\theta $
as the unique projection invariant under the subgroup of the Weyl group fixing
$p_\theta :\mathfrak {a}\to \mathfrak {a}_\theta $
as the unique projection invariant under the subgroup of the Weyl group fixing
![]() $\mathfrak a_\theta $
pointwise. Set
$\mathfrak a_\theta $
pointwise. Set
![]() $\mu _{\theta } := p_{\theta } \circ \mu $
.
$\mu _{\theta } := p_{\theta } \circ \mu $
.
The
![]() $\mathfrak a$
-valued Busemann map
$\mathfrak a$
-valued Busemann map
![]() $\beta : \mathcal F\times G \times G \to \mathfrak a $
is defined as follows: for
$\beta : \mathcal F\times G \times G \to \mathfrak a $
is defined as follows: for
![]() $\xi \in \mathcal F$
and
$\xi \in \mathcal F$
and
![]() $g, h\in G$
,
$g, h\in G$
,
where
![]() $\sigma (g^{-1},\xi )\in \mathfrak a$
is the unique element such that
$\sigma (g^{-1},\xi )\in \mathfrak a$
is the unique element such that
![]() $g^{-1}k \in K \exp (\sigma (g^{-1}, \xi )) N$
for any
$g^{-1}k \in K \exp (\sigma (g^{-1}, \xi )) N$
for any
![]() $k\in K$
with
$k\in K$
with
![]() $\xi =kP$
. For
$\xi =kP$
. For
![]() $\xi =kP_\theta \in \mathcal F_\theta $
for
$\xi =kP_\theta \in \mathcal F_\theta $
for
![]() $k\in K$
, we define the
$k\in K$
, we define the
![]() $\mathfrak a_{\theta }$
-valued Busemann map
$\mathfrak a_{\theta }$
-valued Busemann map
![]() $\beta ^{\theta } : \mathcal F_{\theta } \times G \times G \to \mathfrak a_{\theta }$
as
$\beta ^{\theta } : \mathcal F_{\theta } \times G \times G \to \mathfrak a_{\theta }$
as
this is well defined [Reference Quint19, §6].
In the rest of this section, let
![]() $\Gamma < G$
be a Zariski dense
$\Gamma < G$
be a Zariski dense
![]() $\theta $
-transverse subgroup as in Definition 1.3. For a
$\theta $
-transverse subgroup as in Definition 1.3. For a
![]() $(\Gamma , \theta )$
-proper linear form
$(\Gamma , \theta )$
-proper linear form
![]() $\psi \in \mathfrak a_\theta ^*$
, we denote by
$\psi \in \mathfrak a_\theta ^*$
, we denote by
![]() $\delta _\psi \in (0, \infty ]$
the abscissa of convergence of the series
$\delta _\psi \in (0, \infty ]$
the abscissa of convergence of the series
![]() $\mathcal P_{\psi }(s) := \sum _{\gamma \in \Gamma }e^{-s \psi (\mu _{\theta }(\gamma ))}$
; this is well defined [Reference Kim, Oh and Wang13, Lemma 4.2]. We set
$\mathcal P_{\psi }(s) := \sum _{\gamma \in \Gamma }e^{-s \psi (\mu _{\theta }(\gamma ))}$
; this is well defined [Reference Kim, Oh and Wang13, Lemma 4.2]. We set
Note that
![]() $\psi \circ \operatorname {i}$
can be regarded as a linear form on
$\psi \circ \operatorname {i}$
can be regarded as a linear form on
![]() $\mathfrak a_{\operatorname {i}(\theta )}$
. Using the property that
$\mathfrak a_{\operatorname {i}(\theta )}$
. Using the property that
![]() $\operatorname {i} (\mu (g))=\mu (g^{-1})$
for all
$\operatorname {i} (\mu (g))=\mu (g^{-1})$
for all
![]() $g\in G$
, we deduce that
$g\in G$
, we deduce that
![]() $\mathcal P_{\psi } = \mathcal P_{\psi \circ \operatorname {i}}$
and hence
$\mathcal P_{\psi } = \mathcal P_{\psi \circ \operatorname {i}}$
and hence
![]() $\psi \in \mathcal D_{\Gamma }^{\theta }$
if and only if
$\psi \in \mathcal D_{\Gamma }^{\theta }$
if and only if
![]() ${\psi \circ \operatorname {i} \in \mathcal D_{\Gamma }^{\operatorname {i}(\theta )}}$
.
${\psi \circ \operatorname {i} \in \mathcal D_{\Gamma }^{\operatorname {i}(\theta )}}$
.
The
![]() $\theta $
-limit set
$\theta $
-limit set
![]() $\Lambda _{\theta }$
of
$\Lambda _{\theta }$
of
![]() $\Gamma $
is the unique
$\Gamma $
is the unique
![]() $\Gamma $
-minimal subset of
$\Gamma $
-minimal subset of
![]() $\mathcal F_{\theta }$
[Reference Benoist1]. We also write
$\mathcal F_{\theta }$
[Reference Benoist1]. We also write
The following ergodic property of Patterson–Sullivan measures was obtained by Canary, Zhang, and Zimmer [Reference Canary, Zhang and Zimmer4] (see also [Reference Kim, Oh and Wang13, Reference Kim, Oh and Wang14]).
Theorem 2.1. [Reference Canary, Zhang and Zimmer4, Proposition 9.1, Corollary 11.1]
Suppose that
![]() $\theta =\operatorname {i}(\theta )$
. Let
$\theta =\operatorname {i}(\theta )$
. Let
![]() $\Gamma <G$
be a Zariski dense
$\Gamma <G$
be a Zariski dense
![]() $\theta $
-transverse subgroup. For any
$\theta $
-transverse subgroup. For any
![]() $\psi \in \mathcal D_{\Gamma }^{\theta }$
, there exists a unique
$\psi \in \mathcal D_{\Gamma }^{\theta }$
, there exists a unique
![]() $(\Gamma , \psi )$
-Patterson–Sullivan measure
$(\Gamma , \psi )$
-Patterson–Sullivan measure
![]() $\nu _\psi $
on
$\nu _\psi $
on
![]() $\Lambda _{\theta }$
and
$\Lambda _{\theta }$
and
![]() $\nu _\psi $
is non-atomic. Moreover, the diagonal
$\nu _\psi $
is non-atomic. Moreover, the diagonal
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $(\Lambda _{\theta }^{(2)}, (\nu _\psi \times \nu _{\psi \circ \operatorname {i}})|_{\Lambda _{\theta }^{(2)}})$
is ergodic.
$(\Lambda _{\theta }^{(2)}, (\nu _\psi \times \nu _{\psi \circ \operatorname {i}})|_{\Lambda _{\theta }^{(2)}})$
is ergodic.
3. A property of convergence group actions
In this section, we prove a certain property of convergence group actions which we will need in the proof of our main theorem in the next section. We refer to [Reference Bowditch2] for basic properties of convergence group actions. Let
![]() $\Gamma $
be a countable group acting on a compact metrizable space X (with
$\Gamma $
be a countable group acting on a compact metrizable space X (with
![]() $\# X\ge 3$
) by homeomorphisms. This action is called a convergence group action if for any sequence of distinct elements
$\# X\ge 3$
) by homeomorphisms. This action is called a convergence group action if for any sequence of distinct elements
![]() $\gamma _n \in \Gamma $
, there exist a subsequence
$\gamma _n \in \Gamma $
, there exist a subsequence
![]() $\gamma _{n_k}$
and
$\gamma _{n_k}$
and
![]() $a, b \in X$
such that as
$a, b \in X$
such that as
![]() $k \to \infty $
,
$k \to \infty $
,
![]() $\gamma _{n_k}(x) $
converges to
$\gamma _{n_k}(x) $
converges to
![]() $ a $
for all
$ a $
for all
![]() $x\in X-\{b\}$
, uniformly on compact subsets. In this case, we say
$x\in X-\{b\}$
, uniformly on compact subsets. In this case, we say
![]() $\Gamma $
acts on X as a convergence group, which we suppose in the following. Any element
$\Gamma $
acts on X as a convergence group, which we suppose in the following. Any element
![]() $\gamma \in \Gamma $
of infinite order fixes precisely one or two points of X, and
$\gamma \in \Gamma $
of infinite order fixes precisely one or two points of X, and
![]() $\gamma $
is called parabolic or loxodromic accordingly. In that case, there exist
$\gamma $
is called parabolic or loxodromic accordingly. In that case, there exist
![]() $a_{\gamma }, b_{\gamma } \in X$
, fixed by
$a_{\gamma }, b_{\gamma } \in X$
, fixed by
![]() $\gamma $
, such that
$\gamma $
, such that
![]() $\gamma ^n|_{X- \{b_{\gamma }\}} \to a_\gamma $
uniformly on compact subsets as
$\gamma ^n|_{X- \{b_{\gamma }\}} \to a_\gamma $
uniformly on compact subsets as
![]() $n \to \infty $
. We have
$n \to \infty $
. We have
![]() $\gamma $
loxodromic if and only if
$\gamma $
loxodromic if and only if
![]() $a_{\gamma }\ne b_{\gamma }$
, in which case
$a_{\gamma }\ne b_{\gamma }$
, in which case
![]() $a_{\gamma }$
and
$a_{\gamma }$
and
![]() $b_\gamma $
are called the attracting and repelling fixed points of
$b_\gamma $
are called the attracting and repelling fixed points of
![]() $\gamma $
, respectively.
$\gamma $
, respectively.
We will use the following lemma in the next section.
Lemma 3.1. Let
![]() $\Gamma $
be a torsion-free countable group acting on a compact metric space X as a convergence group. For any compact subset W of X with at least two points, the subgroup
$\Gamma $
be a torsion-free countable group acting on a compact metric space X as a convergence group. For any compact subset W of X with at least two points, the subgroup
![]() $\Gamma _W = \{\gamma \in \Gamma : \gamma W = W\}$
acts on
$\Gamma _W = \{\gamma \in \Gamma : \gamma W = W\}$
acts on
![]() $X- W$
properly discontinuously, that is, for any
$X- W$
properly discontinuously, that is, for any
![]() $\eta \in X - W$
, there exists an open neighborhood U of
$\eta \in X - W$
, there exists an open neighborhood U of
![]() $\eta $
such that
$\eta $
such that
![]() $\gamma U \cap U \neq \emptyset $
for
$\gamma U \cap U \neq \emptyset $
for
![]() $\gamma \in \Gamma _W$
implies
$\gamma \in \Gamma _W$
implies
![]() $\gamma = e$
.
$\gamma = e$
.
Proof. Suppose not. Then there exist
![]() $\eta \in X - W$
, a decreasing sequence of open neighborhoods
$\eta \in X - W$
, a decreasing sequence of open neighborhoods
![]() $U_n$
of
$U_n$
of
![]() $\eta $
in X with
$\eta $
in X with
![]() $\bigcap _n U_n=\{\eta \}$
, and a sequence
$\bigcap _n U_n=\{\eta \}$
, and a sequence
![]() $e\ne \gamma _n\in \Gamma $
such that
$e\ne \gamma _n\in \Gamma $
such that
![]() $\gamma _n W=W$
and
$\gamma _n W=W$
and
![]() $\gamma _n U_n \cap U_n \neq \emptyset $
for each
$\gamma _n U_n \cap U_n \neq \emptyset $
for each
![]() $n\in \mathbb N$
. Hence, there exists a sequence
$n\in \mathbb N$
. Hence, there exists a sequence
![]() $\eta _n \in U_n\cap \gamma _n^{-1}U_n$
; so
$\eta _n \in U_n\cap \gamma _n^{-1}U_n$
; so
![]() $\eta _n \to \eta $
and
$\eta _n \to \eta $
and
![]() $\gamma _n \eta _n \to \eta $
as
$\gamma _n \eta _n \to \eta $
as
![]() $n \to \infty $
.
$n \to \infty $
.
We claim that the elements
![]() $\gamma _n$
are all pairwise distinct, possibly after passing to a subsequence. Otherwise, it would mean that, after passing to a subsequence,
$\gamma _n$
are all pairwise distinct, possibly after passing to a subsequence. Otherwise, it would mean that, after passing to a subsequence,
![]() $\gamma _n$
terms are a constant sequence, say
$\gamma _n$
terms are a constant sequence, say
![]() $\gamma _n = \gamma \ne e$
. Since
$\gamma _n = \gamma \ne e$
. Since
![]() $\gamma \eta = \lim _n \gamma _n \eta _n = \eta $
,
$\gamma \eta = \lim _n \gamma _n \eta _n = \eta $
,
![]() $\eta $
must be a fixed point of
$\eta $
must be a fixed point of
![]() $\gamma $
. Since
$\gamma $
. Since
![]() $\Gamma $
is torsion-free,
$\Gamma $
is torsion-free,
![]() $\gamma $
is either parabolic or loxodromic, and in particular it has at most two fixed points in X, including
$\gamma $
is either parabolic or loxodromic, and in particular it has at most two fixed points in X, including
![]() $\eta $
. Since
$\eta $
. Since
![]() $\eta \not \in W$
and W has at least two points, we can take
$\eta \not \in W$
and W has at least two points, we can take
![]() $w \in W$
which is not fixed by
$w \in W$
which is not fixed by
![]() $\gamma $
. Then, as
$\gamma $
. Then, as
![]() $n\to +\infty $
,
$n\to +\infty $
,
![]() $\gamma ^n w\to \eta $
or
$\gamma ^n w\to \eta $
or
![]() $\gamma ^{-n}w\to \eta $
. Since W is a compact subset such that
$\gamma ^{-n}w\to \eta $
. Since W is a compact subset such that
![]() $\gamma W=W$
and
$\gamma W=W$
and
![]() $\eta \notin W$
, this yields a contradiction.
$\eta \notin W$
, this yields a contradiction.
Therefore, we may assume that
![]() $\{\gamma _n\}$
is an infinite sequence of distinct elements. Since the action of
$\{\gamma _n\}$
is an infinite sequence of distinct elements. Since the action of
![]() $\Gamma $
on X is a convergence group action, there exist a subsequence
$\Gamma $
on X is a convergence group action, there exist a subsequence
![]() $\gamma _{n_k}$
and
$\gamma _{n_k}$
and
![]() $a, b \in X$
such that as
$a, b \in X$
such that as
![]() $k\to \infty $
,
$k\to \infty $
,
![]() $\gamma _{n_k}(x)$
converges to
$\gamma _{n_k}(x)$
converges to
![]() $ a$
for all
$ a$
for all
![]() $x\in X - \{b\}$
, uniformly on compact subsets. There are two cases to consider. Suppose that
$x\in X - \{b\}$
, uniformly on compact subsets. There are two cases to consider. Suppose that
![]() $b=\eta $
. Then
$b=\eta $
. Then
![]() $W \subset X - \{b\}$
, and hence
$W \subset X - \{b\}$
, and hence
![]() $\gamma _{n_k}W \to a$
uniformly as
$\gamma _{n_k}W \to a$
uniformly as
![]() $k \to \infty $
. Since
$k \to \infty $
. Since
![]() $\gamma _{n_k} W = W$
and W is a compact subset, it follows that
$\gamma _{n_k} W = W$
and W is a compact subset, it follows that
![]() $W=\{a\}$
, which contradicts the hypothesis that W consists of at least two elements. Now suppose that
$W=\{a\}$
, which contradicts the hypothesis that W consists of at least two elements. Now suppose that
![]() $b \neq \eta $
. Since
$b \neq \eta $
. Since
![]() $\eta _{n_k}$
converges to
$\eta _{n_k}$
converges to
![]() $ \eta $
, we may assume that
$ \eta $
, we may assume that
![]() $\eta _{n_k} \neq b$
for all k. Noting that
$\eta _{n_k} \neq b$
for all k. Noting that
![]() $\# W \ge 2$
, we can take
$\# W \ge 2$
, we can take
![]() $w_0 \in W - \{b\}$
. If we now consider the following compact subset:
$w_0 \in W - \{b\}$
. If we now consider the following compact subset:
we then have
![]() $\gamma _{n_k} W_0 \to a$
uniformly as
$\gamma _{n_k} W_0 \to a$
uniformly as
![]() $k \to \infty $
. Since
$k \to \infty $
. Since
![]() $\eta _{n_k} \in W_0$
for each k and
$\eta _{n_k} \in W_0$
for each k and
![]() ${\gamma _{n_k}\eta _{n_k} \to \eta} $
as
${\gamma _{n_k}\eta _{n_k} \to \eta} $
as
![]() $k \to \infty $
, we must have
$k \to \infty $
, we must have
However, since
![]() $w_0 \in W_0\cap W$
,
$w_0 \in W_0\cap W$
,
![]() $\gamma _{n_k} w_0 \to \eta $
as
$\gamma _{n_k} w_0 \to \eta $
as
![]() $k \to \infty $
. This implies
$k \to \infty $
. This implies
![]() $\eta \in W$
since W is compact and
$\eta \in W$
since W is compact and
![]() $\gamma _{n_k}w_0\in W$
, yielding a contradiction to the hypothesis
$\gamma _{n_k}w_0\in W$
, yielding a contradiction to the hypothesis
![]() $\eta \notin W$
. This completes the proof.
$\eta \notin W$
. This completes the proof.
We denote by
![]() $\Lambda _X$
the set of all accumulation points of a
$\Lambda _X$
the set of all accumulation points of a
![]() $\Gamma $
-orbit in X. If
$\Gamma $
-orbit in X. If
![]() $\#\Lambda _X\ge 3$
, the
$\#\Lambda _X\ge 3$
, the
![]() $\Gamma $
-action is called non-elementary and
$\Gamma $
-action is called non-elementary and
![]() $\Lambda _X$
is the unique
$\Lambda _X$
is the unique
![]() $\Gamma $
-minimal subset [Reference Bowditch2].
$\Gamma $
-minimal subset [Reference Bowditch2].
A well-known example of a convergence group action is given by a word hyperbolic group
![]() $\Gamma $
. Fix a finite symmetric generating subset
$\Gamma $
. Fix a finite symmetric generating subset
![]() $S_{\Gamma }$
of
$S_{\Gamma }$
of
![]() $\Gamma $
. A geodesic ray in
$\Gamma $
. A geodesic ray in
![]() $\Gamma $
is an infinite sequence
$\Gamma $
is an infinite sequence
![]() $(\gamma _i)_{i=0}^{\infty }$
of elements of
$(\gamma _i)_{i=0}^{\infty }$
of elements of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\gamma _i^{-1}\gamma _{i+1}\in S_{\Gamma }$
for all
$\gamma _i^{-1}\gamma _{i+1}\in S_{\Gamma }$
for all
![]() $i\ge 0$
. The Gromov boundary
$i\ge 0$
. The Gromov boundary
![]() $\partial \Gamma $
is the set of equivalence classes of geodesic rays, where two rays are equivalent to each other if and only if their Hausdorff distance is finite. The group
$\partial \Gamma $
is the set of equivalence classes of geodesic rays, where two rays are equivalent to each other if and only if their Hausdorff distance is finite. The group
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() $\partial \Gamma $
by
$\partial \Gamma $
by
![]() $\gamma \cdot [(\gamma _i)]=[(\gamma \gamma _i)]$
. This action is known to be a convergence group action [Reference Bowditch2, Lemma 1.11].
$\gamma \cdot [(\gamma _i)]=[(\gamma \gamma _i)]$
. This action is known to be a convergence group action [Reference Bowditch2, Lemma 1.11].
Another important example of a convergence group action is the action of a
![]() $\theta $
-transverse subgroup
$\theta $
-transverse subgroup
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda _{\theta \cup \operatorname {i}(\theta )}$
.
$\Lambda _{\theta \cup \operatorname {i}(\theta )}$
.
Proposition 3.2. [Reference Kapovich, Leeb and Porti10, Theorem 4.21]
For a
![]() $\theta $
-transverse subgroup
$\theta $
-transverse subgroup
![]() $\Gamma $
, the action of
$\Gamma $
, the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda _{\theta \cup \operatorname {i}(\theta )}$
is a convergence group action.
$\Lambda _{\theta \cup \operatorname {i}(\theta )}$
is a convergence group action.
4. Non-concentration property
We fix a non-empty subset
![]() $\theta \subset \Pi $
. We first prove the following proposition from which we will deduce Theorem 1.4.
$\theta \subset \Pi $
. We first prove the following proposition from which we will deduce Theorem 1.4.
Proposition 4.1. Let
![]() $\Gamma < G$
be a torsion-free Zariski dense discrete subgroup admitting a convergence group action on a compact metrizable space X. We assume that this action is
$\Gamma < G$
be a torsion-free Zariski dense discrete subgroup admitting a convergence group action on a compact metrizable space X. We assume that this action is
![]() $\theta $
-antipodal in the sense that there exist
$\theta $
-antipodal in the sense that there exist
![]() $\Gamma $
-equivariant homeomorphisms
$\Gamma $
-equivariant homeomorphisms
![]() $f_{\theta } : \Lambda _X \to \Lambda _{\theta }$
and
$f_{\theta } : \Lambda _X \to \Lambda _{\theta }$
and
![]() $f_{\operatorname {i}(\theta )} : \Lambda _X \to \Lambda _{\operatorname {i}(\theta )}$
such that for any
$f_{\operatorname {i}(\theta )} : \Lambda _X \to \Lambda _{\operatorname {i}(\theta )}$
such that for any
![]() $\xi \ne \eta $
in
$\xi \ne \eta $
in
![]() $\Lambda _X$
,
$\Lambda _X$
,
Let
![]() $\nu $
be a
$\nu $
be a
![]() $\Gamma $
-quasi-invariant measure on
$\Gamma $
-quasi-invariant measure on
![]() $\Lambda _{\theta }$
such that:
$\Lambda _{\theta }$
such that:
-
(1)
 $\nu $
is non-atomic;
$\nu $
is non-atomic; -
(2)
 $\Gamma $
acts ergodically on
$\Gamma $
acts ergodically on
 $(\Lambda _{\theta }^{(2)}, (\nu \times \nu _{\operatorname {i}})|_{\Lambda _\theta ^{(2)}})$
for some
$(\Lambda _{\theta }^{(2)}, (\nu \times \nu _{\operatorname {i}})|_{\Lambda _\theta ^{(2)}})$
for some
 $\Gamma $
-quasi-invariant measure
$\Gamma $
-quasi-invariant measure
 $\nu _{\operatorname {i}}$
on
$\nu _{\operatorname {i}}$
on
 $\Lambda _{\operatorname {i}(\theta )}$
.
$\Lambda _{\operatorname {i}(\theta )}$
.
Then, for any proper algebraic subset S of
![]() $\mathcal F_{\theta }$
, we have
$\mathcal F_{\theta }$
, we have
Proof. We first claim that the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $(\Lambda _\theta \times \Lambda _{\operatorname {i}(\theta )}, \nu \times \nu _{{\operatorname {i}}})$
is ergodic. Set
$(\Lambda _\theta \times \Lambda _{\operatorname {i}(\theta )}, \nu \times \nu _{{\operatorname {i}}})$
is ergodic. Set
![]() $R:=(\Lambda _\theta \times \Lambda _{\operatorname {i}(\theta )} ) - \Lambda _\theta ^{(2)}$
. Since the
$R:=(\Lambda _\theta \times \Lambda _{\operatorname {i}(\theta )} ) - \Lambda _\theta ^{(2)}$
. Since the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $(\Lambda _{\theta }^{(2)}, (\nu \times \nu _{\operatorname {i}})|_{\Lambda _\theta ^{(2)}})$
is ergodic, it suffices to show that
$(\Lambda _{\theta }^{(2)}, (\nu \times \nu _{\operatorname {i}})|_{\Lambda _\theta ^{(2)}})$
is ergodic, it suffices to show that
For
![]() $y\in \Lambda _{\operatorname {i}(\theta )}$
, let
$y\in \Lambda _{\operatorname {i}(\theta )}$
, let
![]() $R(y):=\{x\in \Lambda _{\theta } : (x,y) \in R\}$
. By the antipodal property of the pair
$R(y):=\{x\in \Lambda _{\theta } : (x,y) \in R\}$
. By the antipodal property of the pair
![]() $(f_\theta , f_{\operatorname {i}(\theta )})$
, we have that for each
$(f_\theta , f_{\operatorname {i}(\theta )})$
, we have that for each
![]() $y\in \Lambda _{\operatorname {i}(\theta )}$
, we have
$y\in \Lambda _{\operatorname {i}(\theta )}$
, we have
![]() $R(y)=\emptyset $
or
$R(y)=\emptyset $
or
![]() $R(y)= \{(f_{\theta } \circ f_{\operatorname {i}(\theta )}^{-1})(y)\}$
and hence
$R(y)= \{(f_{\theta } \circ f_{\operatorname {i}(\theta )}^{-1})(y)\}$
and hence
![]() $\nu ( R(y))=0$
by the non-atomicity of
$\nu ( R(y))=0$
by the non-atomicity of
![]() $\nu $
.
$\nu $
.
Therefore,
 $$ \begin{align} (\nu\times\nu_{{\operatorname{i}}})(R)=\int_{y\in \Lambda_{\operatorname{i}(\theta)}}\nu (R(y))\,d\nu_{\operatorname{i}}(y)=0, \end{align} $$
$$ \begin{align} (\nu\times\nu_{{\operatorname{i}}})(R)=\int_{y\in \Lambda_{\operatorname{i}(\theta)}}\nu (R(y))\,d\nu_{\operatorname{i}}(y)=0, \end{align} $$
proving the claim.
Now suppose that
![]() $\nu (S)> 0$
for some proper algebraic subset
$\nu (S)> 0$
for some proper algebraic subset
![]() $S \subset \mathcal F_{\theta }$
. We may assume that S is irreducible and of minimal dimension among all such algebraic subsets of
$S \subset \mathcal F_{\theta }$
. We may assume that S is irreducible and of minimal dimension among all such algebraic subsets of
![]() $\mathcal F_\theta $
. Let
$\mathcal F_\theta $
. Let
![]() $W = f_{\theta }^{-1}(S\cap \Lambda _\theta ) \subset \Lambda _X$
. Since
$W = f_{\theta }^{-1}(S\cap \Lambda _\theta ) \subset \Lambda _X$
. Since
![]() $\nu $
is non-atomic and
$\nu $
is non-atomic and
![]() $\nu (S)> 0$
, we have
$\nu (S)> 0$
, we have
![]() $\# W = \infty> 2$
. This implies
$\# W = \infty> 2$
. This implies
![]() $\#\Lambda _X\ge 3$
. By the property of a non-elementary convergence group action,
$\#\Lambda _X\ge 3$
. By the property of a non-elementary convergence group action,
![]() $\Lambda _X$
is the unique
$\Lambda _X$
is the unique
![]() $\Gamma $
-minimal subset of X and there always exists a loxodromic element of
$\Gamma $
-minimal subset of X and there always exists a loxodromic element of
![]() $\Gamma $
[Reference Bowditch2].
$\Gamma $
[Reference Bowditch2].
Since
![]() $\Gamma < G$
is Zariski dense,
$\Gamma < G$
is Zariski dense,
![]() $\Lambda _\theta $
is Zariski dense in
$\Lambda _\theta $
is Zariski dense in
![]() $\mathcal F_\theta $
as well, and hence
$\mathcal F_\theta $
as well, and hence
![]() $\Lambda _{\theta } \not \subset S$
. Therefore,
$\Lambda _{\theta } \not \subset S$
. Therefore,
![]() $X - W$
is a non-empty open subset intersecting
$X - W$
is a non-empty open subset intersecting
![]() $\Lambda _X$
. Since
$\Lambda _X$
. Since
![]() $\Gamma $
acts minimally on
$\Gamma $
acts minimally on
![]() $\Lambda _X$
and the set of attracting fixed points of loxodromic elements of
$\Lambda _X$
and the set of attracting fixed points of loxodromic elements of
![]() $\Gamma $
is a non-empty
$\Gamma $
is a non-empty
![]() $\Gamma $
-invariant subset, there exists a loxodromic element
$\Gamma $
-invariant subset, there exists a loxodromic element
![]() $\gamma _0 \in \Gamma $
whose attracting fixed point
$\gamma _0 \in \Gamma $
whose attracting fixed point
![]() $a_{\gamma _0}$
is contained in
$a_{\gamma _0}$
is contained in
![]() $\Lambda _X- W$
. Hence, applying Lemma 3.1 to
$\Lambda _X- W$
. Hence, applying Lemma 3.1 to
![]() $\eta =a_{\gamma _0}$
, we have an open neighborhood
$\eta =a_{\gamma _0}$
, we have an open neighborhood
![]() $U $
of
$U $
of
![]() $a_{\gamma _0}$
in
$a_{\gamma _0}$
in
![]() $\Lambda _X$
such that
$\Lambda _X$
such that
for all non-trivial
![]() $\gamma \in \Gamma $
with
$\gamma \in \Gamma $
with
![]() $\gamma W = W$
.
$\gamma W = W$
.
Since
![]() $\gamma _0^m|_{\Lambda _X - \{b_{\gamma _0} \}} \to a_{\gamma _0}$
uniformly on compact subsets as
$\gamma _0^m|_{\Lambda _X - \{b_{\gamma _0} \}} \to a_{\gamma _0}$
uniformly on compact subsets as
![]() $m \to +\infty $
and
$m \to +\infty $
and
![]() $\#\Lambda _X\ge 3$
, U contains a point
$\#\Lambda _X\ge 3$
, U contains a point
![]() $\xi \in \Lambda _X-\{a_{\gamma _0}, b_{\gamma _0}\}$
. By replacing
$\xi \in \Lambda _X-\{a_{\gamma _0}, b_{\gamma _0}\}$
. By replacing
![]() $\gamma _0$
by a large power
$\gamma _0$
by a large power
![]() $\gamma _0^m$
if necessary, we can find an open neighborhood V of
$\gamma _0^m$
if necessary, we can find an open neighborhood V of
![]() $\xi $
contained in
$\xi $
contained in
![]() $U-\{a_{\gamma _0}\}$
such that
$U-\{a_{\gamma _0}\}$
such that
![]() $\gamma _0 V \subset U$
and
$\gamma _0 V \subset U$
and
![]() $\gamma _0 V \cap V = \emptyset $
.
$\gamma _0 V \cap V = \emptyset $
.
We now consider the subset
of
![]() $\mathcal F_{\theta } \times \mathcal F_{\operatorname {i}(\theta )}$
. Since
$\mathcal F_{\theta } \times \mathcal F_{\operatorname {i}(\theta )}$
. Since
![]() $\nu (S)> 0$
and
$\nu (S)> 0$
and
![]() $\nu _{\operatorname {i}}(f_{\operatorname {i}(\theta )}(V))> 0$
, we have that
$\nu _{\operatorname {i}}(f_{\operatorname {i}(\theta )}(V))> 0$
, we have that
![]() $\Gamma (S \times f_{\operatorname {i}(\theta )}(V))$
has full
$\Gamma (S \times f_{\operatorname {i}(\theta )}(V))$
has full
![]() $\nu \times \nu _{\operatorname {i}}$
-measure by the ergodicity of the
$\nu \times \nu _{\operatorname {i}}$
-measure by the ergodicity of the
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $(\Lambda _{\theta } \times \Lambda _{\operatorname {i}(\theta )}, \nu \times \nu _{\operatorname {i}})$
. Since
$(\Lambda _{\theta } \times \Lambda _{\operatorname {i}(\theta )}, \nu \times \nu _{\operatorname {i}})$
. Since
![]() $(\nu \times \nu _{\operatorname {i}})(S \times \gamma _0 f_{\operatorname {i}(\theta )}(V))> 0$
, there exists
$(\nu \times \nu _{\operatorname {i}})(S \times \gamma _0 f_{\operatorname {i}(\theta )}(V))> 0$
, there exists
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
In particular, we have
Since S was chosen to be of minimal dimension and irreducible among proper algebraic sets with positive
![]() $\nu $
-measure, we must have
$\nu $
-measure, we must have
![]() $S = \gamma S$
. It follows from the
$S = \gamma S$
. It follows from the
![]() $\Gamma $
-invariance of
$\Gamma $
-invariance of
![]() $\Lambda _{\theta }$
that
$\Lambda _{\theta }$
that
![]() $W = \gamma W$
.
$W = \gamma W$
.
The
![]() $\Gamma $
-equivariance of
$\Gamma $
-equivariance of
![]() $f_{\operatorname {i}(\theta )}$
implies that
$f_{\operatorname {i}(\theta )}$
implies that
Since
![]() $\gamma _0 V \cap V = \emptyset $
, we have
$\gamma _0 V \cap V = \emptyset $
, we have
![]() $\gamma \neq e$
. Hence, it follows from
$\gamma \neq e$
. Hence, it follows from
![]() $V \subset U$
,
$V \subset U$
,
![]() $\gamma _0 V \subset U$
, and the choice in equation (4.2) of U that
$\gamma _0 V \subset U$
, and the choice in equation (4.2) of U that
which gives a contradiction to equation (4.3). This finishes the proof.
4.1. Proof of Theorem 1.4
Let
![]() $\Gamma < G$
be a Zariski dense
$\Gamma < G$
be a Zariski dense
![]() $\theta $
-transverse subgroup and
$\theta $
-transverse subgroup and
![]() $\nu $
a
$\nu $
a
![]() $(\Gamma , \psi )$
-Patterson–Sullivan measure for a
$(\Gamma , \psi )$
-Patterson–Sullivan measure for a
![]() $(\Gamma , \theta )$
-proper linear form
$(\Gamma , \theta )$
-proper linear form
![]() $\psi \in \mathfrak a_{\theta }^*$
such that
$\psi \in \mathfrak a_{\theta }^*$
such that
![]() $\sum _{\gamma \in \Gamma } e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
. We may assume without loss of generality that
$\sum _{\gamma \in \Gamma } e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
. We may assume without loss of generality that
![]() $\Gamma $
is torsion-free. Indeed, let
$\Gamma $
is torsion-free. Indeed, let
![]() $\Gamma _0 < \Gamma $
be a torsion-free subgroup of finite index. Then
$\Gamma _0 < \Gamma $
be a torsion-free subgroup of finite index. Then
![]() $\Gamma _0$
is also a Zariski dense
$\Gamma _0$
is also a Zariski dense
![]() $\theta $
-transverse subgroup of G. Moreover,
$\theta $
-transverse subgroup of G. Moreover,
![]() $\nu $
is a
$\nu $
is a
![]() $(\Gamma _0, \psi )$
-Patterson–Sullivan measure since the limit sets for
$(\Gamma _0, \psi )$
-Patterson–Sullivan measure since the limit sets for
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma _0$
are the same. Write
$\Gamma _0$
are the same. Write
![]() $\Gamma = \bigcup _{i = 1}^n \gamma _i \Gamma _0$
for some
$\Gamma = \bigcup _{i = 1}^n \gamma _i \Gamma _0$
for some
![]() $\gamma _1, \ldots , \gamma _n \in \Gamma $
. By [Reference Benoist1, Lemma 4.6], there exists
$\gamma _1, \ldots , \gamma _n \in \Gamma $
. By [Reference Benoist1, Lemma 4.6], there exists
![]() $C> 0$
such that
$C> 0$
such that
![]() $\| \mu (\gamma _i \gamma ) - \mu (\gamma )\| \le C$
for all
$\| \mu (\gamma _i \gamma ) - \mu (\gamma )\| \le C$
for all
![]() $\gamma \in \Gamma _0$
and
$\gamma \in \Gamma _0$
and
![]() $i = 1, \ldots , n$
. Hence, we have that
$i = 1, \ldots , n$
. Hence, we have that
![]() $\psi $
is
$\psi $
is
![]() $(\Gamma _0, \theta )$
-proper as well and
$(\Gamma _0, \theta )$
-proper as well and
 $$ \begin{align*}\infty = \sum_{\gamma \in \Gamma} e^{-\psi(\mu_{\theta}(\gamma))} = \sum_{i = 1}^n \sum_{\gamma \in \Gamma_0} e^{-\psi(\mu_{\theta}(\gamma_i \gamma))} \le n e^{\|\psi\| C} \sum_{\gamma \in \Gamma_0} e^{-\psi(\mu_{\theta}(\gamma))},\end{align*} $$
$$ \begin{align*}\infty = \sum_{\gamma \in \Gamma} e^{-\psi(\mu_{\theta}(\gamma))} = \sum_{i = 1}^n \sum_{\gamma \in \Gamma_0} e^{-\psi(\mu_{\theta}(\gamma_i \gamma))} \le n e^{\|\psi\| C} \sum_{\gamma \in \Gamma_0} e^{-\psi(\mu_{\theta}(\gamma))},\end{align*} $$
where
![]() $\|\psi \|$
denotes the operator norm of
$\|\psi \|$
denotes the operator norm of
![]() $\psi $
. In particular,
$\psi $
. In particular,
![]() $\sum _{\gamma \in \Gamma _0} e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
. Therefore, replacing
$\sum _{\gamma \in \Gamma _0} e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
. Therefore, replacing
![]() $\Gamma $
by
$\Gamma $
by
![]() $\Gamma _0$
, we assume that
$\Gamma _0$
, we assume that
![]() $\Gamma $
is torsion-free. By Proposition 3.2, the action of
$\Gamma $
is torsion-free. By Proposition 3.2, the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\Lambda _{\theta \cup \operatorname {i}(\theta )}$
is a convergence group action.
$\Lambda _{\theta \cup \operatorname {i}(\theta )}$
is a convergence group action.
Since there exists a
![]() $(\Gamma , \psi )$
-conformal measure, we have
$(\Gamma , \psi )$
-conformal measure, we have
![]() $\delta _{\psi } \le 1$
by [Reference Kim, Oh and Wang13, Lemma 7.3]. Therefore, the hypothesis
$\delta _{\psi } \le 1$
by [Reference Kim, Oh and Wang13, Lemma 7.3]. Therefore, the hypothesis
![]() $\sum _{\gamma \in \Gamma } e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
implies that
$\sum _{\gamma \in \Gamma } e^{-\psi (\mu _{\theta }(\gamma ))} = \infty $
implies that
![]() $\psi \in \mathcal D_{\Gamma }^{\theta }$
. Moreover, the
$\psi \in \mathcal D_{\Gamma }^{\theta }$
. Moreover, the
![]() $\theta $
-antipodality of
$\theta $
-antipodality of
![]() $\Gamma $
implies that the canonical projections
$\Gamma $
implies that the canonical projections
are
![]() $\Gamma $
-equivariant
$\Gamma $
-equivariant
![]() $\theta $
-antipodal homeomorphisms [Reference Kim, Oh and Wang13, Lemma 9.5]. This implies that Theorem 2.1 indeed holds for a general
$\theta $
-antipodal homeomorphisms [Reference Kim, Oh and Wang13, Lemma 9.5]. This implies that Theorem 2.1 indeed holds for a general
![]() $\theta $
without the hypothesis
$\theta $
without the hypothesis
![]() $\theta =\operatorname {i}(\theta )$
. Hence,
$\theta =\operatorname {i}(\theta )$
. Hence,
![]() $\nu =\nu _\psi $
,
$\nu =\nu _\psi $
,
![]() $\nu _\psi $
is non-atomic, and the diagonal
$\nu _\psi $
is non-atomic, and the diagonal
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $(\Lambda _{\theta }^{(2)}, (\nu _\psi \times \nu _{\psi \circ \operatorname {i}})|_{\Lambda _{\theta }^{(2)}})$
is ergodic. Since
$(\Lambda _{\theta }^{(2)}, (\nu _\psi \times \nu _{\psi \circ \operatorname {i}})|_{\Lambda _{\theta }^{(2)}})$
is ergodic. Since
![]() $\nu _{\psi \circ \operatorname {i}}$
is
$\nu _{\psi \circ \operatorname {i}}$
is
![]() $\Gamma $
-conformal, it is
$\Gamma $
-conformal, it is
![]() $\Gamma $
-quasi-invariant. Therefore, Theorem 1.4 follows from Proposition 4.1.
$\Gamma $
-quasi-invariant. Therefore, Theorem 1.4 follows from Proposition 4.1.
We emphasize again that Lemma 3.1 and Proposition 4.1 were introduced to deal with the case when
![]() $\operatorname {i}$
is non-trivial. Indeed, when
$\operatorname {i}$
is non-trivial. Indeed, when
![]() $\operatorname {i}$
is trivial, Theorem 1.4 follows from the following
$\operatorname {i}$
is trivial, Theorem 1.4 follows from the following
![]() $\theta $
-version of [Reference Edwards, Lee and Oh5, Theorem 9.3].
$\theta $
-version of [Reference Edwards, Lee and Oh5, Theorem 9.3].
Theorem 4.2. Let
![]() $\Gamma < G$
be a Zariski dense discrete subgroup. Let
$\Gamma < G$
be a Zariski dense discrete subgroup. Let
![]() $\nu $
be a
$\nu $
be a
![]() $\Gamma $
-quasi-invariant measure on
$\Gamma $
-quasi-invariant measure on
![]() $\Lambda _{\theta }$
. Suppose that the diagonal
$\Lambda _{\theta }$
. Suppose that the diagonal
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $(\Lambda _{\theta } \times \Lambda _{\theta }, {\nu \times \nu })$
is ergodic. Then, for any proper algebraic subset S of
$(\Lambda _{\theta } \times \Lambda _{\theta }, {\nu \times \nu })$
is ergodic. Then, for any proper algebraic subset S of
![]() $\mathcal F_{\theta }$
, we have
$\mathcal F_{\theta }$
, we have
Proof. The proof is identical to the proof of [Reference Edwards, Lee and Oh5, Theorem 9.3] except that we work with a general
![]() $\theta $
. We reproduce it here for the convenience of the readers. Let S be a proper irreducible subvariety of
$\theta $
. We reproduce it here for the convenience of the readers. Let S be a proper irreducible subvariety of
![]() $\mathcal F_\theta $
with
$\mathcal F_\theta $
with
![]() $\nu (S)>0$
and of minimal dimension. Since
$\nu (S)>0$
and of minimal dimension. Since
![]() ${(\nu \times \nu ) (S\times S)>0}$
, the
${(\nu \times \nu ) (S\times S)>0}$
, the
![]() $\Gamma $
-ergodicity of
$\Gamma $
-ergodicity of
![]() $\nu \times \nu $
implies that
$\nu \times \nu $
implies that
![]() $(\nu \times \nu )(\Gamma (S\times S))=1$
. It follows that for any
$(\nu \times \nu )(\Gamma (S\times S))=1$
. It follows that for any
![]() $\gamma _0\in \Gamma $
, there exists
$\gamma _0\in \Gamma $
, there exists
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
![]() $(S \times \gamma _0S)\cap (\gamma S\times \gamma S)$
has positive
$(S \times \gamma _0S)\cap (\gamma S\times \gamma S)$
has positive
![]() $\nu \times \nu $
-measure; hence,
$\nu \times \nu $
-measure; hence,
![]() $\nu (S\cap \gamma S)>0$
and
$\nu (S\cap \gamma S)>0$
and
![]() $\nu (\gamma _0 S\cap \gamma S)>0$
. Since S is irreducible and of minimal dimension, it follows that
$\nu (\gamma _0 S\cap \gamma S)>0$
. Since S is irreducible and of minimal dimension, it follows that
![]() $S=\gamma S=\gamma _0 S$
. Since
$S=\gamma S=\gamma _0 S$
. Since
![]() $\gamma _0\in \Gamma $
was arbitrary, we have
$\gamma _0\in \Gamma $
was arbitrary, we have
![]() $\Gamma S=S$
, which contradicts the Zariski density hypothesis on
$\Gamma S=S$
, which contradicts the Zariski density hypothesis on
![]() $\Gamma $
.
$\Gamma $
.
We finally mention that the proof of Proposition 4.1 implies the following when the second measure cannot be taken to be the same as the first measure.
Theorem 4.3. Let
![]() $\Gamma < G$
be a Zariski dense torsion-free discrete subgroup acting on
$\Gamma < G$
be a Zariski dense torsion-free discrete subgroup acting on
![]() $\Lambda _\theta $
as a convergence group. Let
$\Lambda _\theta $
as a convergence group. Let
![]() $\nu $
be a non-atomic
$\nu $
be a non-atomic
![]() $\Gamma $
-quasi-invariant measure on
$\Gamma $
-quasi-invariant measure on
![]() $\Lambda _{\theta }$
. Suppose that the diagonal
$\Lambda _{\theta }$
. Suppose that the diagonal
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $(\Lambda _{\theta } \times \Lambda _{\theta }, \nu \times \nu ')$
is ergodic for some
$(\Lambda _{\theta } \times \Lambda _{\theta }, \nu \times \nu ')$
is ergodic for some
![]() $\Gamma $
-quasi-invariant measure
$\Gamma $
-quasi-invariant measure
![]() $\nu '$
on
$\nu '$
on
![]() $\Lambda _\theta $
. Then, for any proper algebraic subset S of
$\Lambda _\theta $
. Then, for any proper algebraic subset S of
![]() $\mathcal F_{\theta }$
, we have
$\mathcal F_{\theta }$
, we have
Proof. Since
![]() $\Gamma $
acts ergodically on the entire product space
$\Gamma $
acts ergodically on the entire product space
![]() $(\Lambda _{\theta } \times \Lambda _{\theta }, \nu \times \nu ')$
, the first part of the proof of Proposition 4.1 is not relevant. Suppose that S is an irreducible proper subvariety of
$(\Lambda _{\theta } \times \Lambda _{\theta }, \nu \times \nu ')$
, the first part of the proof of Proposition 4.1 is not relevant. Suppose that S is an irreducible proper subvariety of
![]() $\mathcal F_\theta $
and of minimal dimension among all subvarieties with positive
$\mathcal F_\theta $
and of minimal dimension among all subvarieties with positive
![]() $\nu $
-measure. Then, setting
$\nu $
-measure. Then, setting
![]() $W = S \cap \Lambda _{\theta }$
, as in the proof of Proposition 4.1, we can find non-empty open subsets
$W = S \cap \Lambda _{\theta }$
, as in the proof of Proposition 4.1, we can find non-empty open subsets
![]() $V\subset U\subset \Lambda _\theta - W$
such that
$V\subset U\subset \Lambda _\theta - W$
such that
![]() $ \gamma U \cap U = \emptyset $
for all non-trivial
$ \gamma U \cap U = \emptyset $
for all non-trivial
![]() $\gamma \in \Gamma $
with
$\gamma \in \Gamma $
with
![]() $\gamma W = W$
, and
$\gamma W = W$
, and
![]() $\gamma _0V\subset U$
and
$\gamma _0V\subset U$
and
![]() $\gamma _0V\cap V=\emptyset $
for some
$\gamma _0V\cap V=\emptyset $
for some
![]() $\gamma _0\in \Gamma $
. Using
$\gamma _0\in \Gamma $
. Using
![]() $(\nu \times \nu ')(S\times V)>0$
, we then get a contradiction by the same argument as in Proposition 4.1.
$(\nu \times \nu ')(S\times V)>0$
, we then get a contradiction by the same argument as in Proposition 4.1.
Acknowledgements
We would like to thank Subhadip Dey for helpful conversations. H.O. is partially supported by the NSF grant No. DMS-1900101.