Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-31T12:04:33.261Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-singular 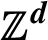$\mathbb {Z}^d$-actions: an ergodic theorem over rectangles with application to the critical dimensions

Part of: Ergodic theory

Published online by Cambridge University Press:  02 December 2020

ANTHONY H. DOOLEY  and
KIERAN JARRETT
ANTHONY H. DOOLEY
Affiliation:
School of Mathematical and Physical Sciences, University of Technology Sydney, NSW 2007, Australia (e-mail: Anthony.Dooley@uts.edu.au)
KIERAN JARRETT*
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath, BA2 7AY, UK
*
e-mail: K.Jarrett@bath.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We adapt techniques developed by Hochman to prove a non-singular ergodic theorem for 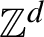$\mathbb {Z}^d$-actions where the sums are over rectangles with side lengths increasing at arbitrary rates, and in particular are not necessarily balls of a norm. This result is applied to show that the critical dimensions with respect to sequences of such rectangles are invariants of metric isomorphism. These invariants are calculated for the natural action of 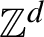$\mathbb {Z}^d$ on a product of d measure spaces.

Keywords

classical ergodic theorygroup actionscritical dimensions

MSC classification

Primary: 37A40: Nonsingular (and infinite-measure preserving) transformations
Secondary: 37A35: Entropy and other invariants, isomorphism, classification 37A15: General groups of measure-preserving transformations

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 12 , December 2021 , pp. 3722 - 3739
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory ( Mathematical Surveys and Monographs , 50). American Mathematical Society, Providence, RI, 1997.10.1090/surv/050CrossRefGoogle Scholar
de Guzmán, M.. Differentiation of integrals in ${R}^n$ ( Lecture Notes in Mathematics , 481). Springer, Berlin, 1975. With appendices by A. Córdoba and R. Fefferman, and two by R. Moriyón.Google Scholar
Dooley, A. H. and Mortiss, G.. On the critical dimension and AC entropy for Markov odometers. Monatsh. Math. 149(3) (2006), 193–213.CrossRefGoogle Scholar
Dooley, A. H. and Mortiss, G.. The critical dimensions of Hamachi shifts. Tohoku Math. J. (2) 59(1) (2007), 57–66.CrossRefGoogle Scholar
Dooley, A. H. and Mortiss, G.. On the critical dimensions of product odometers. Ergod. Th. & Dynam. Sys. 29(2) (2009), 475–485.10.1017/S0143385708000606CrossRefGoogle Scholar
Feldman, J.. A ratio ergodic theorem for commuting, conservative, invertible transformations with quasi-invariant measure summed over symmetric hypercubes. Ergod. Th. & Dynam. Sys. 27(4) (2007), 1135–1142.10.1017/S0143385707000119CrossRefGoogle Scholar
Hochman, M.. A ratio ergodic theorem for multiparameter non-singular actions. J. Eur. Math. Soc. (JEMS) 12(2) (2010), 365–383.10.4171/JEMS/201CrossRefGoogle Scholar
Krengel, U.. Ergodic Theorems ( de Gruyter Studies in Mathematics , 6). Walter de Gruyter & Co., Berlin, 1985. With a supplement by A. Brunel.10.1515/9783110844641CrossRefGoogle Scholar
Mortiss, G.. An invariant for non-singular isomorphism. Ergod. Th. & Dynam. Sys. 23(3) (2003), 885–893.CrossRefGoogle Scholar