No CrossRef data available.
Article contents
A non-singular version of the Oseledeč ergodic theorem
Part of:
Ergodic theory
Published online by Cambridge University Press: 24 February 2022
Abstract
Kingman’s subadditive ergodic theorem is traditionally proved in the setting of a measure-preserving invertible transformation T of a measure space 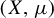 $(X, \mu )$. We use a theorem of Silva and Thieullen to extend the theorem to the setting of a not necessarily invertible transformation, which is non-singular under the assumption that
$(X, \mu )$. We use a theorem of Silva and Thieullen to extend the theorem to the setting of a not necessarily invertible transformation, which is non-singular under the assumption that 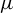 $\mu $ and
$\mu $ and 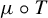 $\mu \circ T$ have the same null sets. Using this, we are able to produce versions of the Furstenberg–Kesten theorem and the Oseledeč ergodic theorem for products of random matrices without the assumption that the transformation is either invertible or measure-preserving.
$\mu \circ T$ have the same null sets. Using this, we are able to produce versions of the Furstenberg–Kesten theorem and the Oseledeč ergodic theorem for products of random matrices without the assumption that the transformation is either invertible or measure-preserving.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
Aaronson, J.. An Introduction to Infinite Ergodic Theory. American Mathematical Society, Providence, RI, 1997.CrossRefGoogle Scholar
Avila, A. and Bochi, J.. On the subadditive ergodic theorem. Preprint, 2009, http://www.mat.uc.cl/~jairo.bochi/docs/kingbirk.pdf.Google Scholar
Birkhoff, G. D.. Proof of the ergodic theorem. Proc. Natl. Acad. Sci. USA 17 (1931), 656–660.CrossRefGoogle ScholarPubMed
Dooley, A. H. and Mortiss, G.. On the critical dimension of product odometers. Ergod. Th. & Dynam. Sys. 29 (2008), 475–485.CrossRefGoogle Scholar
Furstenberg, H. and Kesten, H.. Products of random matrices. Ann. Math. Stat. 31 (1960), 457–469.CrossRefGoogle Scholar
Hurewicz, W.. Ergodic theorem without invariant measure. Ann. of Math. (2) 45 (1944), 192–206.CrossRefGoogle Scholar
Jones, R. L.. New proofs for the maximal ergodic theorem and the Hardy–Littlewood maximal theorem. Proc. Amer. Math. Soc. 87 (1983), 681–684.CrossRefGoogle Scholar
Katznelson, Y. and Weiss, B.. A simple proof of some ergodic theorems. Israel J. Math. 42 (1982), 291–296.CrossRefGoogle Scholar
Kingman, J. F. C.. The ergodic theory of subadditive stochastic processes. J. R. Stat. Soc. Ser. B. 30 (1968), 499–510.Google Scholar
Oseledets, I.. A multiplicative ergodic theorem: Lyapunov characteristic numbers for dynamical systems. Trans. Moscow Math. Soc. 19 (1968), 197–231.Google Scholar
Raghunathan, M. S.. A proof of Oseledec’s multiplicative ergodic theorem. Israel J. Math. 32 (1979), 356–362.CrossRefGoogle Scholar
Schmidt, K.. Algebraic Ideas in Ergodic Theory (CBMS Regional Conference Series in Mathematics, 76). American Mathematical Society, Providence, RI, 1990.CrossRefGoogle Scholar
Silva, C. E. and Thieullen, P.. The subadditive ergodic theorem and recurrence properties of Markovian transformations. J. Math. Anal. Appl. 154 (1991), 83–99.CrossRefGoogle Scholar
Steel, J. M.. Kingman’s subadditive ergodic theorem. Ann. Inst. Henri Poincaré Probab. Stat. 25 (1989), 93–98.Google Scholar


