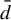 ${\bar d}$-approachability, entropy density and
${\bar d}$-approachability, entropy density and 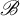 $\mathscr {B}$-free shifts
$\mathscr {B}$-free shiftsPublished online by Cambridge University Press: 15 February 2022
We study approximation schemes for shift spaces over a finite alphabet using (pseudo)metrics connected to Ornstein’s
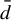 ${\bar d}$
metric. This leads to a class of shift spaces we call
${\bar d}$
metric. This leads to a class of shift spaces we call
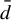 ${\bar d}$
-approachable. A shift space is
${\bar d}$
-approachable. A shift space is
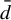 ${\bar d}$
-approachable when its canonical sequence of Markov approximations converges to it also in the
${\bar d}$
-approachable when its canonical sequence of Markov approximations converges to it also in the
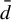 ${\bar d}$
sense. We give a topological characterization of chain-mixing
${\bar d}$
sense. We give a topological characterization of chain-mixing
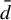 ${\bar d}$
-approachable shift spaces. As an application we provide a new criterion for entropy density of ergodic measures. Entropy density of a shift space means that every invariant measure
${\bar d}$
-approachable shift spaces. As an application we provide a new criterion for entropy density of ergodic measures. Entropy density of a shift space means that every invariant measure
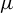 $\mu $
of such a shift space is the weak
$\mu $
of such a shift space is the weak
 $^*$
limit of a sequence
$^*$
limit of a sequence
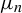 $\mu _n$
of ergodic measures with the corresponding sequence of entropies
$\mu _n$
of ergodic measures with the corresponding sequence of entropies
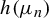 $h(\mu _n)$
converging to
$h(\mu _n)$
converging to
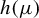 $h(\mu )$
. We prove ergodic measures are entropy-dense for every shift space that can be approximated in the
$h(\mu )$
. We prove ergodic measures are entropy-dense for every shift space that can be approximated in the
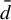 ${\bar d}$
pseudometric by a sequence of transitive sofic shifts. This criterion can be applied to many examples that were beyond the reach of previously known techniques including hereditary
${\bar d}$
pseudometric by a sequence of transitive sofic shifts. This criterion can be applied to many examples that were beyond the reach of previously known techniques including hereditary
 $\mathscr {B}$
-free shifts and some minimal or proximal systems. The class of symbolic dynamical systems covered by our results includes also shift spaces where entropy density was established previously using the (almost) specification property.
$\mathscr {B}$
-free shifts and some minimal or proximal systems. The class of symbolic dynamical systems covered by our results includes also shift spaces where entropy density was established previously using the (almost) specification property.