Article contents
On equicontinuous factors of flows on locally path-connected compact spaces
Published online by Cambridge University Press: 13 November 2020
Abstract
We consider a locally path-connected compact metric space K with finite first Betti number 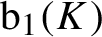 $\textrm {b}_1(K)$ and a flow
$\textrm {b}_1(K)$ and a flow 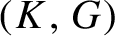 $(K, G)$ on K such that G is abelian and all G-invariant functions
$(K, G)$ on K such that G is abelian and all G-invariant functions 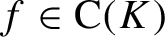 $f\,{\in}\, \textrm{C}(K)$ are constant. We prove that every equicontinuous factor of the flow
$f\,{\in}\, \textrm{C}(K)$ are constant. We prove that every equicontinuous factor of the flow 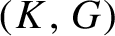 $(K, G)$ is isomorphic to a flow on a compact abelian Lie group of dimension less than
$(K, G)$ is isomorphic to a flow on a compact abelian Lie group of dimension less than 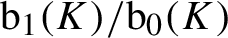 ${\textrm {b}_1(K)}/{\textrm {b}_0(K)}$. For this purpose, we use and provide a new proof for Theorem 2.12 of Hauser and Jäger [Monotonicity of maximal equicontinuous factors and an application to toral flows. Proc. Amer. Math. Soc. 147 (2019), 4539–4554], which states that for a flow on a locally connected compact space the quotient map onto the maximal equicontinuous factor is monotone, i.e., has connected fibers. Our alternative proof is a simple consequence of a new characterization of the monotonicity of a quotient map
${\textrm {b}_1(K)}/{\textrm {b}_0(K)}$. For this purpose, we use and provide a new proof for Theorem 2.12 of Hauser and Jäger [Monotonicity of maximal equicontinuous factors and an application to toral flows. Proc. Amer. Math. Soc. 147 (2019), 4539–4554], which states that for a flow on a locally connected compact space the quotient map onto the maximal equicontinuous factor is monotone, i.e., has connected fibers. Our alternative proof is a simple consequence of a new characterization of the monotonicity of a quotient map 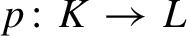 $p\colon K\to L$ between locally connected compact spaces K and L that we obtain by characterizing the local connectedness of K in terms of the Banach lattice
$p\colon K\to L$ between locally connected compact spaces K and L that we obtain by characterizing the local connectedness of K in terms of the Banach lattice 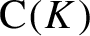 $\textrm {C}(K)$.
$\textrm {C}(K)$.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 2
- Cited by


