No CrossRef data available.
Article contents
On sofic approximations of 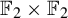 ${\mathbb F}_2\times {\mathbb F}_2$
${\mathbb F}_2\times {\mathbb F}_2$
Published online by Cambridge University Press: 04 May 2021
Abstract
We construct a sofic approximation of 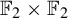 ${\mathbb F}_2\times {\mathbb F}_2$ that is not essentially a ‘branched cover’ of a sofic approximation by homomorphisms. This answers a question of L. Bowen.
${\mathbb F}_2\times {\mathbb F}_2$ that is not essentially a ‘branched cover’ of a sofic approximation by homomorphisms. This answers a question of L. Bowen.
MSC classification
Secondary:
20F69: Asymptotic properties of groups
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
Alon, N., Lubotzky, A. and Widgerson, A.. Semi-direct product in groups and zig-zag product in graphs: connections and applications (extended abstract). Proc. 42nd IEEE Symp. on Foundations of Computer Science (Las Vegas, NV, 2001). IEEE Computer Society, Los Alamitos, CA, 2001, pp. 630–637.Google Scholar
Arzhantseva, G. and Paunescu, L.. Almost commuting permutations are near commuting permutations. J. Funct. Anal. 269(3) (2015), 745–757.CrossRefGoogle Scholar
Bowen, L.. Examples in the entropy theory of countable group actions. Ergod. Th. & Dynam. Sys. 40(10) (2020), 2593–2680.CrossRefGoogle Scholar
Bowen, L.. A brief introduction to sofic entropy theory. Proc. Int. Congress of Mathematicians (Rio de Janeiro, 2018). Vol. 2. World Scientific, Hackensack, NJ, 2019, pp. 1847–1866.CrossRefGoogle Scholar
Bourgain, J. and Varjú, P.. Expansion in SLd
(ℤ/qℤ), q arbitrary. Invent. Math. 188(1) (2012), 151–173.CrossRefGoogle Scholar
Elek, G. and Szabó, E.. Sofic representations of amenable groups. Proc. Amer. Math. Soc. 139 (2011), 4285–4291.CrossRefGoogle Scholar
Ioana, A.. Compact actions whose orbit equivalence relations are not profinite. Adv. Math. 354 (2019), 106753, 19 pp.CrossRefGoogle Scholar
Ioana, A.. Stability for product groups and propert (τ). J. Funct. Anal. 279(9) (2020), 108729.CrossRefGoogle Scholar
Lazarovich, N., Levit, A. and Minsky, Y.. Surface groups are flexibly stable. Preprint, 2019, arXiv:1901.07182.Google Scholar
Lubotzky, A. and Segal, D.. Subgroup Growth (Progress in Mathematics, 212). Birkhäuser, Basel, 2003.CrossRefGoogle Scholar
Lubotzky, A.. Discrete Groups, Expanding Graphs and Invariant Measures (Progress in Mathematics, 125). Birkhäuser, Basel, 1994. With an Appendix by Jonathan D. Rogawski.CrossRefGoogle Scholar
Arzhantseva, G., Thom, A. and Valette, A.. Finite-dimensional approximation of discrete groups. Oberwolfach Rep. 8(2) (2011), 1429–1467 (English summary). Abstracts from the workshop held on May 15–21, 2011.CrossRefGoogle Scholar
Thom, A.. Finitary approximations of groups and their applications. Proc. Int. Congress of Mathematics (Rio de Janeiro, 2018). Vol. 2. World Scientific, Hackensack, NJ, 2019, pp. 1775–1796.Google Scholar


