Article contents
On some generalizations of skew-shifts on 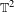 $\mathbb{T}^{2}$
$\mathbb{T}^{2}$
Published online by Cambridge University Press: 04 May 2017
Abstract
In this paper we investigate maps of the two-torus 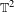 $\mathbb{T}^{2}$ of the form
$\mathbb{T}^{2}$ of the form 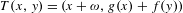 $T(x,y)=(x+\unicode[STIX]{x1D714},g(x)+f(y))$ for Diophantine
$T(x,y)=(x+\unicode[STIX]{x1D714},g(x)+f(y))$ for Diophantine 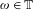 $\unicode[STIX]{x1D714}\in \mathbb{T}$ and for a class of maps
$\unicode[STIX]{x1D714}\in \mathbb{T}$ and for a class of maps 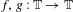 $f,g:\mathbb{T}\rightarrow \mathbb{T}$, where each
$f,g:\mathbb{T}\rightarrow \mathbb{T}$, where each  $g$ is strictly monotone and of degree 2 and each
$g$ is strictly monotone and of degree 2 and each 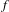 $f$ is an orientation-preserving circle homeomorphism. For our class of
$f$ is an orientation-preserving circle homeomorphism. For our class of 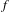 $f$ and
$f$ and  $g$, we show that
$g$, we show that  $T$ is minimal and has exactly two invariant and ergodic Borel probability measures. Moreover, these measures are supported on two
$T$ is minimal and has exactly two invariant and ergodic Borel probability measures. Moreover, these measures are supported on two  $T$-invariant graphs. One of the graphs is a strange non-chaotic attractor whose basin of attraction consists of (Lebesgue) almost all points in
$T$-invariant graphs. One of the graphs is a strange non-chaotic attractor whose basin of attraction consists of (Lebesgue) almost all points in 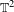 $\mathbb{T}^{2}$. Only a low-regularity assumption (Lipschitz) is needed on the maps
$\mathbb{T}^{2}$. Only a low-regularity assumption (Lipschitz) is needed on the maps 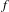 $f$ and
$f$ and  $g$, and the results are robust with respect to Lipschitz-small perturbations of
$g$, and the results are robust with respect to Lipschitz-small perturbations of 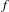 $f$ and
$f$ and  $g$.
$g$.
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 1
- Cited by

