Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ward, Thomas
1994.
Automorphisms ofZd-subshifts of finite type.
Indagationes Mathematicae,
Vol. 5,
Issue. 4,
p.
495.
Ward, Thomas
1998.
A Family of Markov Shifts (Almost) Classified by Periodic Points.
Journal of Number Theory,
Vol. 71,
Issue. 1,
p.
1.
Bhattacharya, Siddhartha
2003.
Zero-entropy algebraic $\mathbb {Z}\sp d$-actions that do not exhibit rigidity.
Duke Mathematical Journal,
Vol. 116,
Issue. 3,
Roettger, C.G.J.
2005.
Periodic points classify a family of Markov shifts.
Journal of Number Theory,
Vol. 113,
Issue. 1,
p.
69.

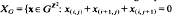 for all
for all 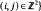 . Let μ
. Let μ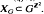 . The group ℤ
. The group ℤ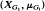 and
and 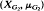 are not measure-theoretically isomorphic. For any finite Abelian groups
are not measure-theoretically isomorphic. For any finite Abelian groups 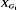 and
and 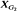 are topologically conjugate if and only if
are topologically conjugate if and only if 