Article contents
On the existence of maximizing measures for irreducible countable Markov shifts: a dynamical proof
Published online by Cambridge University Press: 18 March 2013
Abstract
We prove that if 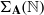 ${\Sigma }_{\mathbf{A} } ( \mathbb{N} )$ is an irreducible Markov shift space over
${\Sigma }_{\mathbf{A} } ( \mathbb{N} )$ is an irreducible Markov shift space over 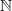 $ \mathbb{N} $ and
$ \mathbb{N} $ and 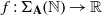 $f: {\Sigma }_{\mathbf{A} } ( \mathbb{N} )\rightarrow \mathbb{R} $ is coercive with bounded variation then there exists a maximizing probability measure for
$f: {\Sigma }_{\mathbf{A} } ( \mathbb{N} )\rightarrow \mathbb{R} $ is coercive with bounded variation then there exists a maximizing probability measure for 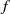 $f$, whose support lies on a Markov subshift over a finite alphabet. Furthermore, the support of any maximizing measure is contained in this same compact subshift. To the best of our knowledge, this is the first proof beyond the finitely primitive case in the general irreducible non-compact setting. It is also noteworthy that our technique works for the full shift over positive real sequences.
$f$, whose support lies on a Markov subshift over a finite alphabet. Furthermore, the support of any maximizing measure is contained in this same compact subshift. To the best of our knowledge, this is the first proof beyond the finitely primitive case in the general irreducible non-compact setting. It is also noteworthy that our technique works for the full shift over positive real sequences.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright ©2013 Cambridge University Press
References
Atkinson, G.. Recurrence of co-cycles and random walks. J. Lond. Math. Soc. 2 (1976), 486–488.Google Scholar
Bissacot, R. and Garibaldi, E.. Weak KAM methods and ergodic optimal problems for countable Markov shifts. Bull. Braz. Math. Soc. 41 (2010), 321–338.Google Scholar
Iommi, G.. Ergodic optimization for renewal type shifts. Monatsh. Math. 150 (2007), 91–95.CrossRefGoogle Scholar
Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. Ser. A 15 (2006), 197–224.Google Scholar
Jenkinson, O., Mauldin, R. D. and Urbański, M.. Zero temperature limits of Gibbs-equilibrium states for countable alphabet subshifts of finite type. J. Stat. Phys. 119 (2005), 765–776.Google Scholar
Jenkinson, O., Mauldin, R. D. and Urbański, M.. Ergodic optimization for countable alphabet subshifts of finite type. Ergod. Th. & Dynam. Sys. 26 (2006), 1791–1803.Google Scholar
Jenkinson, O., Mauldin, R. D. and Urbański, M.. Ergodic optimization for non-compact dynamical systems. Dyn. Syst. 22 (2007), 379–388.Google Scholar
Morris, I. D.. Entropy for zero-temperature limits of Gibbs-equilibrium states for countable-alphabet subshifts of finite type. J. Stat. Phys. 126 (2007), 315–324.Google Scholar
Morris, I. D.. A sufficient condition for the subordination principle in ergodic optimization. Bull. Lond. Math. Soc. 39 (2007), 214–220.Google Scholar
Parthasarathy, K. R.. On the category of ergodic measures. Illinois J. Math. 5 (1961), 648–656.Google Scholar
- 7
- Cited by

