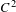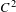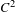Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nakamura, Fumihiko
Nakano, Yushi
Toyokawa, Hisayoshi
and
Yano, Kouji
2023.
Arcsine law for random dynamics with a core.
Nonlinearity,
Vol. 36,
Issue. 3,
p.
1491.