Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T02:20:48.552Z Has data issue: false hasContentIssue false
  • English
  • Français

Period doubling in area-preserving maps: an associated one-dimensional problem

Published online by Cambridge University Press:  02 September 2010

DENIS GAIDASHEV  and
HANS KOCH
DENIS GAIDASHEV
Affiliation:
Department of Mathematics, University of Uppsala, Uppsala, Sweden (email: gaidash@math.uu.se)
HANS KOCH
Affiliation:
Department of Mathematics, University of Texas at Austin, Austin, Texas, USA (email: koch@math.utexas.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

It has been observed that the famous Feigenbaum–Coullet–Tresser period-doubling universality has a counterpart for area-preserving maps of ℝ2. A renormalization approach has been used in a computer-assisted proof of existence of an area-preserving map with orbits of all binary periods in Eckmann et al [Existence of a fixed point of the doubling transformation for area-preserving maps of the plane. Phys. Rev. A 26(1) (1982), 720–722; A computer-assisted proof of universality for area-preserving maps. Mem. Amer. Math. Soc. 47 (1984), 1–121]. As is the case with all non-trivial universality problems in non-dissipative systems in dimensions more than one, no analytic proof of this period-doubling universality exists to date. We argue that the period-doubling renormalization fixed point for area-preserving maps is almost one dimensional, in the sense that it is close to the following Hénon-like (after a coordinate change) map: 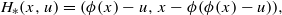where ϕ solves 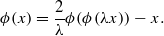We then give a ‘proof’ of existence of solutions of small analytic perturbations of this one-dimensional problem, and describe some of the properties of this solution. The ‘proof’ consists of an analytic argument for factorized inverse branches of ϕ together with verification of several inequalities and inclusions of subsets of ℂ numerically. Finally, we suggest an analytic approach to the full period-doubling problem for area-preserving maps based on its proximity to the one-dimensional case. In this respect, the paper is an exploration of possible analytic machinery for a non-trivial renormalization problem in a conservative two-dimensional system.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 31 , Issue 4 , August 2011 , pp. 1193 - 1228
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[AK]Abad, J. J. and Koch, H.. Renormalization and periodic orbits for Hamiltonian flows. Comm. Math. Phys. 212(2) (2000), 371–394.CrossRefGoogle Scholar
[AKW]Abad, J. J., Koch, H. and Wittwer, P.. A renormalization group for Hamiltonians: numerical results. Nonlinearity 11 (1998), 1185–1194.CrossRefGoogle Scholar
[BCGG]Benettin, G.et al. Universal properties in conservative dynamical systems. Lettere al Nuovo Cimento 28 (1980), 1–4.CrossRefGoogle Scholar
[Bou]Bountis, T.. Period doubling bifurcations and universality in conservative systems. Phys. D 3 (1981), 577–589.CrossRefGoogle Scholar
[CEK1]Collet, P., Eckmann, J.-P. and Koch, H.. Period doubling bifurcations for families of maps on ℝn. J. Stat. Phys. 25(1) (1981), 1–14.CrossRefGoogle Scholar
[CEK2]Collet, P., Eckmann, J.-P. and Koch, H.. On universality for area-preserving maps of the plane. Phys. D 3 (1981), 457–467.CrossRefGoogle Scholar
[dCLM]de Carvalho, A., Lyubich, M. and Martens, M.. Renormalization in the Hénon family, I: universality but non-rigidity. Nonlinearity 11 (1998), 1185–1194.Google Scholar
[dF1]de Faria, E.. Proof of universality for critical circle mappings. Thesis, CUNY, 1992.Google Scholar
[dF2]de Faria, E.. Asymptotic rigidity of scaling ratios for critical circle mappings. Ergod. Th. & Dynam. Sys. 19(4) (1999), 995–1035.CrossRefGoogle Scholar
[DP]Derrida, B. and Pomeau, Y.. Feigenbaum’s ratios of two-dimensional area preserving maps. Phys. Lett. A 80 (1980), 217–219.CrossRefGoogle Scholar
[ED]Escande, D. F. and Doveil, F.. Renormalization method for computing the threshold of the large scale stochastic instability in two degree of freedom Hamiltonian systems. J. Stat. Phys. 26 (1981), 257–284.CrossRefGoogle Scholar
[EKW1]Eckmann, J.-P., Koch, H. and Wittwer, P.. Existence of a fixed point of the doubling transformation for area-preserving maps of the plane. Phys. Rev. A 26(1) (1982), 720–722.CrossRefGoogle Scholar
[EKW2]Eckmann, J.-P., Koch, H. and Wittwer, P.. A computer-assisted proof of universality for area-preserving maps. Mem. Amer. Math. Soc. 47 (1984), 1–121.Google Scholar
[Eps1]Epstein, H.. New proofs of the existence of the Feigenbaum functions. Comm. Math. Phys. 106 (1986), 395–426.CrossRefGoogle Scholar
[Eps2]Epstein, H.. Fixed points of composition operators II. Nonlinearity 2 (1989), 305–310.CrossRefGoogle Scholar
[Fei1]Feigenbaum, M. J.. Quantitative universality for a class of nonlinear transformations. J. Stat. Phys. 19 (1978), 25–52.CrossRefGoogle Scholar
[Fei2]Feigenbaum, M. J.. Universal metric properties of non-linear transformations. J. Stat. Phys. 21 (1979), 669–706.CrossRefGoogle Scholar
[Gai1]Gaidashev, D.. Renormalization of isoenergetically degenerate Hamiltonian flows and associated bifurcations of invariant tori. Discrete Contin. Dyn. Syst. 13(1) (2005), 63–102.CrossRefGoogle Scholar
[GaiYa]Gaidashev, D. and Yampolsky, M.. Cylinder renormalization of Siegel disks. Exp. Math. 16(2) (2007), 215–226.CrossRefGoogle Scholar
[GJ1]Gaidashev, D. and Johnson, T.. Dynamics of the universal area-preserving map associated with period doubling: hyperbolic sets. Nonlinearity 22 (2009), 2487–2520.CrossRefGoogle Scholar
[GJ2]Gaidashev, D. and Johnson, T.. Dynamics of the universal area-preserving map associated with period doubling: stable sets. J. Mod. Dyn. 3(4) (2009), 555–587.CrossRefGoogle Scholar
[GK]Gaidashev, D. and Koch, H.. Renormalization and shearless invariant tori: numerical results. Nonlinearity 17(5) (2004), 1713–1722.CrossRefGoogle Scholar
[Hel]Helleman, R. H. G.. Self-generated chaotic behavior in nonlinear mechanics. Fundamental Problems in Statistical Mechanics. Ed. Cohen, E. G. D.. North-Holland, Amsterdam, 1980, p. 165.Google Scholar
[KLDM]Khanin, K., Lopes Dias, J. and Marklof, J.. Multidimensional continued fractions, dynamic renormalization and KAM theory. Comm. Math. Phys. 270(1) (2007), 197–231.CrossRefGoogle Scholar
[Koch1]Koch, H.. On the renormalization of Hamiltonian flows, and critical invariant tori. Discrete Contin. Dyn. Syst. 8 (2002), 633–646.CrossRefGoogle Scholar
[Koch2]Koch, H.. A renormalization group fixed point associated with the breakup of golden invariant tori. Discrete Contin. Dyn. Syst. 11(4) (2004), 881–909.CrossRefGoogle Scholar
[Koch3]Koch, H.. Existence of critical invariant tori. Ergod. Th. & Dynam. Sys. 28 (2008), 1879–1894.CrossRefGoogle Scholar
[Kocić]Kocić, S.. Renormalization of Hamiltonians for Diophantine frequency vectors and KAM tori. Nonlinearity 18 (2005), 2513–2544.Google Scholar
[Lyu]Lyubich, M.. Feigenbaum–Coullet–Tresser universality and Milnor’s hairness conjecture. Ann. of Math. (2) 149 (1999), 319–420.CrossRefGoogle Scholar
[LY]Lyubich, M. and Yampolsky, M.. Dynamics of quadratic polynomials: complex bounds for real maps. Ann. Inst. Fourier 47(4) (1997), 1219–1255.CrossRefGoogle Scholar
[McK1]MacKay, R. S.. Renormalization approach to invariant circles in area-preserving maps. Phys. D 7 (1983), 283–300.CrossRefGoogle Scholar
[McK2]MacKay, R. S.. Renormalisation in area preserving maps. Thesis, Princeton, NJ, 1982. World Scientific, London, 1993.Google Scholar
[McM]McMullen, C.. Self-similarity of Siegel disks and Hausdorff dimension of Julia sets. Acta Math. 180 (1998), 247–292.CrossRefGoogle Scholar
[ME]Mehr, A. and Escande, D. F.. Destruction of KAM tori in Hamiltonian systems: link with the destabilization of nearby cycles and calculation of residues. Phys. D 13(3) (1984), 302–338.CrossRefGoogle Scholar
[Prog] Programs available at http://math.uu.se/∼gaidash/Programs/doubling.tar.gz.Google Scholar
[SK]Shenker, S. J. and Kadanoff, L. P.. Critical behaviour of KAM surfaces. I. Empirical results. J. Stat. Phys. 27 (1982), 631–656.CrossRefGoogle Scholar
[Spa]Sparrow, C.. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors. Springer, New York, 1982.CrossRefGoogle Scholar
[Sul]Sullivan, D.. Bounds, quadratic differentials and renormalization conjectures. Mathematics into the Twenty-first Century, AMS Centennial Publications, Vol. II. American Mathematical Society, Providence, RI, 1992, pp. 417–466.Google Scholar
[TC]Tresser, C. and Coullet, P.. Itérations d’endomorphismes et groupe de renormalisation. C. R. Acad. Sci. Paris 287A (1978), 577–580.Google Scholar
[Val]Valiron, G.. Fonctions Analytiques. Presses Universitaires de France, Paris, 1954.Google Scholar
[Ya1]Yampolsky, M.. Hyperbolicity of renormalization of critical circle maps. Publ. Math. Inst. Hautes Études Sci. 96 (2002), 1–41.Google Scholar
[Ya2]Yampolsky, M.. Renormalization horseshoe for critical circle maps. Comm. Math. Phys. 240 (2003), 75–96.CrossRefGoogle Scholar
[Ya3]Yampolsky, M.. Siegel disks and renormalization fixed points. Holomorphic Dynamics and Renormalization (Fields Institute Communications, 53). American Mathematical Society, Providence, RI, 2008, pp. 377–393.Google Scholar