Hostname: page-component-76c49bb84f-h2dfl Total loading time: 0 Render date: 2025-07-13T21:51:58.454Z Has data issue: false hasContentIssue false
  • English
  • Français

Periodic expansion of one by Salem numbers

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Low-dimensional dynamical systems Topological dynamics

Published online by Cambridge University Press:  14 October 2022

SHIGEKI AKIYAMA Open the ORCID record for SHIGEKI AKIYAMA [Opens in a new window]  and
HACHEM HICHRI
SHIGEKI AKIYAMA*
Affiliation:
Institute of Mathematics, University of Tsukuba, 1-1-1 Tennodai, Tsukuba, Ibaraki 305-8571, Japan
HACHEM HICHRI
Affiliation:
Département de Mathématiques (UR18ES15), Faculté des sciences de Monastir, Université de Monastir, Monastir 5019, Tunisie (e-mail: hichemhichri@yahoo.fr)
*
e-mail: akiyama@math.tsukuba.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for a Salem number 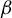$\beta $ of degree d, there exists a positive constant 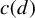$c(d)$ where 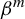$\beta ^m$ is a Parry number for integers m of natural density 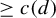$\ge c(d)$. Further, we show 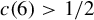$c(6)>1/2$ and discuss a relation to the discretized rotation in dimension 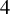$4$.

Keywords

beta expansionperiodicitySalem numberdiscretized rotation

MSC classification

Primary: 37E05: Maps of the interval (piecewise continuous, continuous, smooth) 37B10: Symbolic dynamics 11K16: Normal numbers, radix expansions, Pisot numbers, Salem numbers, good lattice points, etc.

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 9 , September 2023 , pp. 2841 - 2862
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Akiyama, S.. Pisot numbers and greedy algorithm. Number Theory (Eger, 1996). Eds. Győry, K., Pethő, A. and Sós, V.. de Gruyter, Berlin, 1998, pp. 9–21.Google Scholar
Akiyama, S.. Pisot number system and its dual tiling. Physics and Theoretical Computer Science (Amsterdam) (NATO Security through Science Series - D: Information and Communication Security, 7). Eds. Gazeau, J.-P., Nešetřil, J. and Rovan, B.. IOS Press, Amsterdam, 2007, pp. 133–154.Google Scholar
Akiyama, S.. A family of non-sofic beta expansions. Ergod. Th. & Dynam. Sys. 36(2) (2016), 343–354.CrossRefGoogle Scholar
Akiyama, S., Borbély, T., Brunotte, H., Pethő, A. and Thuswaldner, J. M.. Generalized radix representations and dynamical systems I. Acta Math. Hungar. 108(3) (2005), 207–238.10.1007/s10474-005-0221-zCrossRefGoogle Scholar
Akiyama, S., Brunotte, H., Pethő, A. and Steiner, W.. Periodicity of certain piecewise affine planar maps. Tsukuba J. Math. 32(1) (2008), 1–55.CrossRefGoogle Scholar
Akiyama, S. and Kwon, D. Y.. Constructions of Pisot and Salem numbers with flat palindromes. Monatsh. Math. 155(3–4) (2008), 265–275.CrossRefGoogle Scholar
Bertin, M.-J., Decomps-Guilloux, A., Grandet-Hugot, M., Pathiaux-Delefosse, M. and Schreiber, J.-P.. Pisot and Salem Numbers. Birkhäuser, Basel. 1992.10.1007/978-3-0348-8632-1CrossRefGoogle Scholar
Bertrand, A.. Développement en base de Pisot et répartition modulo 1. C. R. Acad. Sci. Paris Sér. I Math. 285 (1977), 419–421.Google Scholar
Blanchard, F.. $\beta$ -expansion and symbolic dynamics. Theoret. Comput. Sci. 65 (1989), 131–141.CrossRefGoogle Scholar
Boyarsky, A. and Góra, P.. Laws of Chaos (Probability and Its Applications). Birkhäuser Boston, Inc., Boston, MA, 1997.CrossRefGoogle Scholar
Boyd, D. W.. Salem numbers of degree four have periodic expansions. Number Theory. Walter de Gruyter, Berlin, 1989, pp. 57–64.Google Scholar
Boyd, D. W.. On the beta expansion for Salem numbers of degree 6. Math. Comp. 65 (1996), 861–875.10.1090/S0025-5718-96-00700-4CrossRefGoogle Scholar
Dubickas, A. and Jankauskas, J.. Linear relations with conjugates of a Salem number. J. Théor. Nombres Bordeaux 32(1) (2020), 179–191.CrossRefGoogle Scholar
Frougny, C.. Numeration systems. Algebraic Combinatorics on Words. Ed. Lothaire, M.. Cambridge University Press, Cambridge, 1970, Ch. 7.Google Scholar
Hichri, H.. Beta expansion for some particular sequences of Salem numbers. Int. J. Number Theory 10(08) (2014), 2135–2149.CrossRefGoogle Scholar
Hichri, H.. On the beta expansion of Salem numbers of degree 8. LMS J. Comput. Math. 17(01) (2014), 289–301.10.1112/S1461157014000035CrossRefGoogle Scholar
Hichri, H.. Beta expansion of Salem numbers approaching Pisot numbers with the finiteness property. Acta Arith. 168 (2015), 107–119.CrossRefGoogle Scholar
Ito, S. and Takahashi, Y.. Markov subshifts and realization of $\beta$ -expansions. J. Math. Soc. Japan 26(1) (1974), 33–55.10.2969/jmsj/02610033CrossRefGoogle Scholar
Kouptsov, K. L., Lowenstein, J. H. and Vivaldi, F.. Quadratic rational rotations of the torus and dual lattice maps. Nonlinearity 15(6) (2002), 1795–1842.10.1088/0951-7715/15/6/306CrossRefGoogle Scholar
Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences. Wiley, New York, 1974.Google Scholar
Lowenstein, J., Hatjispyros, S. and Vivaldi, F.. Quasi-periodicity, global stability and scaling in a model of Hamiltonian round-off. Chaos 7(1) (1997), 49–66.CrossRefGoogle Scholar
McKee, J. F. and Smyth, C. J.. There are Salem numbers of every trace. Bull. Lond. Math. Soc. 37(1) (2005), 25–36.CrossRefGoogle Scholar
Parry, W.. On the beta-expansions of real numbers. Acta Math. Acad. Sci. Hungary 11 (1960), 401–416.CrossRefGoogle Scholar
Pollicott, M. and Yuri, M.. Dynamical Systems and Ergodic Theory (London Mathematical Society Student Texts, 40). Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
Rényi, A.. Representations for real numbers and their ergodic properties. Acta Math. Hungar. 8 (1957), 477–493.10.1007/BF02020331CrossRefGoogle Scholar
Schmidt, K.. On periodic expansions of Pisot numbers and Salem numbers. Bull. Lond. Math. Soc. 12 (1980), 269–278.CrossRefGoogle Scholar
Smyth, C. J.. Salem numbers of negative trace. Math. Comp. 69 (2000), 827–838.CrossRefGoogle Scholar
Smyth, C. J.. Seventy years of Salem numbers. Bull. Lond. Math. Soc. 47(3) (2015), 379–395.CrossRefGoogle Scholar
Verger-Gaugry, J.-L.. On the dichotomy of Perron numbers and beta-conjugates. Monatsh. Math. 155(3–4) (2008), 277–299.10.1007/s00605-008-0002-1CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer-Verlag, New York, 1982.CrossRefGoogle Scholar