No CrossRef data available.
Article contents
Pointwise convergence in nilmanifolds along smooth functions of polynomial growth
Published online by Cambridge University Press: 25 September 2023
Abstract
We study the equidistribution of orbits of the form 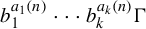 $b_1^{a_1(n)}\cdots b_k^{a_k(n)}\Gamma $ in a nilmanifold X, where the sequences
$b_1^{a_1(n)}\cdots b_k^{a_k(n)}\Gamma $ in a nilmanifold X, where the sequences  $a_i(n)$ arise from smooth functions of polynomial growth belonging to a Hardy field. We show that under certain assumptions on the growth rates of the functions
$a_i(n)$ arise from smooth functions of polynomial growth belonging to a Hardy field. We show that under certain assumptions on the growth rates of the functions  $a_1,\ldots ,a_k$, these orbits are equidistributed on some subnilmanifold of the space X. As an application of these results and in combination with the Host–Kra structure theorem for measure-preserving systems, as well as some recent seminorm estimates of the author for ergodic averages concerning Hardy field functions, we deduce a norm convergence result for multiple ergodic averages. Our method mainly relies on an equidistribution result of Green and Tao on finite segments of polynomial orbits on a nilmanifold [The quantitative behaviour of polynomial orbits on nilmanifolds. Ann. of Math. (2) 175 (2012), 465–540].
$a_1,\ldots ,a_k$, these orbits are equidistributed on some subnilmanifold of the space X. As an application of these results and in combination with the Host–Kra structure theorem for measure-preserving systems, as well as some recent seminorm estimates of the author for ergodic averages concerning Hardy field functions, we deduce a norm convergence result for multiple ergodic averages. Our method mainly relies on an equidistribution result of Green and Tao on finite segments of polynomial orbits on a nilmanifold [The quantitative behaviour of polynomial orbits on nilmanifolds. Ann. of Math. (2) 175 (2012), 465–540].
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press


