Article contents
Polynomial beta functions
Published online by Cambridge University Press: 19 September 2008
Abstract
The pointwise spectral radii of irreducible matrices whose entries are polynomials with positive, integral coefficients are studied in this paper. Most results are derived in the case that the resulting algebraic function, the beta function of S. Tuncel, is in fact a polynomial. We show that the set of beta functions forms a semiring, and the spectral radius of a matrix of beta functions is again a beta function. We also show that the coefficients of a polynomial beta function p must be real algebraic integers, and p satisfies (after a change of variables if necessary) the inequality 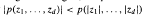 for non-zero (and not all positive) complex numbers z1,…,zd. If
for non-zero (and not all positive) complex numbers z1,…,zd. If 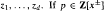 and the ordered sequence of exponents appearing in p is of the form (m,m+1,…,M−,1,M) for some integers m and M, the same inequality is necessary and sufficient for p to be a beta function.
and the ordered sequence of exponents appearing in p is of the form (m,m+1,…,M−,1,M) for some integers m and M, the same inequality is necessary and sufficient for p to be a beta function.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1994
References
REFERENCES
- 3
- Cited by

