Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ledrappier, Fran¸ois
and
Strelcyn, Jean-Marie
1982.
A proof of the estimation from below in Pesin's entropy formula.
Ergodic Theory and Dynamical Systems,
Vol. 2,
Issue. 2,
p.
203.
Young, Lai-Sang
1982.
Dimension, entropy and Lyapunov exponents.
Ergodic Theory and Dynamical Systems,
Vol. 2,
Issue. 1,
p.
109.
Mañé, Ricardo
1983.
On the uniqueness of the maximizing measure for rational maps.
Boletim da Sociedade Brasileira de Matemática,
Vol. 14,
Issue. 1,
p.
27.
Newhouse, S. E.
1983.
Dynamical System and Chaos.
Vol. 179,
Issue. ,
p.
165.
Ledrappier, F.
1984.
Propriétés Ergodiques Des Mesures De Sinaï.
Publications mathématiques de l'IHÉS,
Vol. 59,
Issue. 1,
p.
163.
Kifer, Yuri
1984.
Entropy via random perturbations.
Transactions of the American Mathematical Society,
Vol. 282,
Issue. 2,
p.
589.
Ledrappier, F.
1984.
École d'Été de Probabilités de Saint-Flour XII - 1982.
Vol. 1097,
Issue. ,
p.
305.
Mendoza, Leonardo
1985.
The entropy of C2 surface diffeomorphisms in terms of Hausdorff dimension and a Lyapunov exponent.
Ergodic Theory and Dynamical Systems,
Vol. 5,
Issue. 2,
p.
273.
Przytycki, Feliks
1985.
Hausdorff dimension of harmonic measure on the boundary of an attractive basin for a holomorphic map.
Inventiones Mathematicae,
Vol. 80,
Issue. 1,
p.
161.
Kovachev, Valery
1988.
Smoothness of the billiard ball map for strictly convex domains near the boundary.
Proceedings of the American Mathematical Society,
Vol. 103,
Issue. 3,
p.
856.
Ledrappier, F.
and
Young, L. -S.
1988.
Entropy formula for random transformations.
Probability Theory and Related Fields,
Vol. 80,
Issue. 2,
p.
217.
Mañé, Ricardo
1988.
Dynamical Systems Valparaiso 1986.
Vol. 1331,
Issue. ,
p.
86.
Przytycki, Feliks
1990.
On the Perron-Frobenius-ruelle operator for rational maps on the riemann sphere and for Hölder continuous functions.
Boletim da Sociedade Brasileira de Matemática,
Vol. 20,
Issue. 2,
p.
95.
Hazewinkel, M.
1990.
Encyclopaedia of Mathematics.
p.
67.
Thieullen, P.
1991.
Lyapunov Exponents.
Vol. 1486,
Issue. ,
p.
232.
Thieullen, P.
1992.
Fibres dynamiques. Entropie et dimension.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 9,
Issue. 2,
p.
119.
Hu, Huyi
1993.
Some ergodic properties of commuting diffeomorphisms.
Ergodic Theory and Dynamical Systems,
Vol. 13,
Issue. 1,
p.
73.
Carvalho, Maria
1993.
Sinai–Ruelle–Bowen measures for N-dimensional derived from Anosov diffeomorphisms.
Ergodic Theory and Dynamical Systems,
Vol. 13,
Issue. 1,
p.
21.
Young, L.-S.
1993.
From Topology to Computation: Proceedings of the Smalefest.
p.
201.
Margulis, G. A.
and
Tomanov, G. M.
1994.
Invariant measures for actions of unipotent groups over local fields on homogeneous spaces.
Inventiones Mathematicae,
Vol. 116,
Issue. 1,
p.
347.

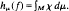 We prove this formula without using the theory of stable manifolds.
We prove this formula without using the theory of stable manifolds.