Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T16:50:26.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Rates in almost sure invariance principle for slowly mixing dynamical systems

Part of: Limit theorems Low-dimensional dynamical systems

Published online by Cambridge University Press:  26 February 2019

C. CUNY ,
J. DEDECKER ,
A. KOREPANOV  and
F. MERLEVÈDE
C. CUNY
Affiliation:
Université de Brest, LMBA, UMR CNRS 6205, France email christophe.cuny@univ-brest.fr
J. DEDECKER
Affiliation:
Université Paris Descartes, Sorbonne Paris Cité, Laboratoire MAP5 (UMR 8145), France email jerome.dedecker@parisdescartes.fr
A. KOREPANOV
Affiliation:
Mathematics Institute, University of Warwick, Coventry, CV4 7AL, UK email a.korepanov@warwick.ac.uk
F. MERLEVÈDE
Affiliation:
Université Paris-Est, LAMA (UMR 8050), UPEM, CNRS, UPEC, France email florence.merlevede@u-pem.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

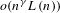We prove the one-dimensional almost sure invariance principle with essentially optimal rates for slowly (polynomially) mixing deterministic dynamical systems, such as Pomeau–Manneville intermittent maps, with Hölder continuous observables. Our rates have form $o(n^{\unicode[STIX]{x1D6FE}}L(n))$, where 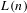$L(n)$ is a slowly varying function and $\unicode[STIX]{x1D6FE}$ is determined by the speed of mixing. We strongly improve previous results where the best available rates did not exceed $O(n^{1/4})$. 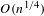To break the $O(n^{1/4})$ barrier, we represent the dynamics as a Young-tower-like Markov chain and adapt the methods of Berkes–Liu–Wu and Cuny–Dedecker–Merlevède on the Komlós–Major–Tusnády approximation for dependent processes.

Keywords

strong invariance principleKMT approximationnon-uniformly expanding dynamical systemsMarkov chain

MSC classification

Primary: 37E05: Maps of the interval (piecewise continuous, continuous, smooth)
Secondary: 60F17: Functional limit theorems; invariance principles
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 9 , September 2020 , pp. 2317 - 2348
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J. and Denker, M.. Local limit theorems for partial sums of stationary sequences generated by Gibbs-Markov maps. Stoch. Dyn. 1(2) (2001), 193–237.10.1142/S0219493701000114Google Scholar
Bennett, G.. Probability inequalities for the sum of independent random variables. J. Amer. Statist. Assoc. 57 (1962), 33–45.10.1080/01621459.1962.10482149Google Scholar
Berkes, I., Liu, W. and Wu, W.. Komlós–Major–Tusnády approximation under dependence. Ann. Probab. 42 (2014), 794–817.10.1214/13-AOP850Google Scholar
Cuny, C., Dedecker, J. and Merlevède, F.. On the Komlós, Major and Tusnády strong approximation for some classes of random iterates. Stochastic Process. Appl. 128(4) (2018), 1347–1385.10.1016/j.spa.2017.07.011Google Scholar
Cuny, C. and Merlevède, F.. Strong invariance principles with rate for ‘reverse’ martingales and applications. J. Theoret. Probab. 28(1) (2015), 137–183.10.1007/s10959-013-0506-zGoogle Scholar
Erdős, P. and Rényi, A.. On Cantor’s series with convergent ∑1/q n. Ann. Univ. Sci. Budapest. Eötvös. Sect. Math. 2 (1959), 93–109.Google Scholar
Gouëzel, S.. Sharp polynomial estimates for the decay of correlations. Israel J. Math. 139 (2004), 29–65.10.1007/BF02787541Google Scholar
Gouëzel, S.. Vitesse de décorrélation et théorèmes limites pour les applications non uniformément dilatantes. PhD Thesis, Orsay, 2004.Google Scholar
Gouëzel, S.. A Borel–Cantelli lemma for intermittent interval maps. Nonlinearity 20 (2007), 1491–1497.10.1088/0951-7715/20/6/010Google Scholar
Hanson, D. L. and Russo, R. P.. Some results on increments of the Wiener process with applications to lag sums of i.i.d. random variables. Ann. Probab. 11(3) (1983), 609–623.10.1214/aop/1176993505Google Scholar
Holland, M.. Slowly mixing systems and intermittency maps. Ergod. Th. & Dynam. Sys. 25 (2005), 133–159.10.1017/S0143385704000343Google Scholar
Hu, H.. Decay of correlations for piecewise smooth maps with indifferent fixed points. Ergod. Th. & Dynam. Sys. 24 (2004), 495–524.10.1017/S0143385703000671Google Scholar
Komlós, J., Major, P. and Tusnády, G.. An approximation of partial sums of independent RV’-s and the sample DF. I. Z. Wahrscheinlichkeitstheor. verw. Geb. 32 (1975), 111–131.10.1007/BF00533093Google Scholar
Komlós, J., Major, P. and Tusnády, G.. An approximation of partial sums of independent RV’-s and the sample DF. II. Z. Wahrscheinlichkeitstheor. verw. Geb. 34 (1976), 34–58.10.1007/BF00532688Google Scholar
Korepanov, A.. Equidistribution for nonuniformly expanding systems. Comm. Math. Phys. 359 (2018), 1123–1138.10.1007/s00220-017-3062-zGoogle Scholar
Korepanov, A.. Rates in almost sure invariance principle for dynamical systems with some hyperbolicity. Comm. Math. Phys. 363 (2018), 173–190.10.1007/s00220-018-3234-5Google Scholar
Korepanov, A., Kosloff, Z. and Melbourne, I.. Martingale-coboundary decomposition for families of dynamical systems. Ann. Inst. H. Poincaré Anal. Non Linéaire 35 (2018), 859–885.10.1016/j.anihpc.2017.08.005Google Scholar
Lindvall, T.. On coupling of discrete renewal processes. Z. Wahrscheinlichkeitstheor. verw. Geb. 48 (1979), 57–70.10.1007/BF00534882Google Scholar
Liverani, C., Saussol, B. and Vaienti, S.. A probabilistic approach to intermittency. Ergod. Th. & Dynam. Sys. 19 (1999), 671–685.10.1017/S0143385799133856Google Scholar
Melbourne, I. and Nicol, M.. Almost sure invariance principle for nonuniformly hyperbolic systems. Comm. Math. Phys. 260 (2005), 131–146.10.1007/s00220-005-1407-5Google Scholar
Melbourne, I. and Nicol, M.. A vector-valued almost sure invariance principle for hyperbolic dynamical systems. Ann. Probab. 37(2) (2009), 478–505.10.1214/08-AOP410Google Scholar
Merlevède, F. and Rio, E.. Strong approximation of partial sums under dependence conditions with application to dynamical systems. Stochastic Process. Appl. 122 (2012), 386–417.10.1016/j.spa.2011.08.012Google Scholar
Merlevède, F. and Rio, E.. Strong approximation for additive functionals of geometrically ergodic Markov chains. Electron. J. Probab. 20 (2015), 1–27.10.1214/EJP.v20-3746Google Scholar
Nummelin, E.. General Irreducible Markov Chains and Nonnegative Operators (Cambridge Tracts in Mathematics, 83). Cambridge University Press, Cambridge, 1984.10.1017/CBO9780511526237Google Scholar
Pomeau, Y. and Manneville, P.. Intermittent transition to turbulence in dissipative dynamical systems. Comm. Math. Phys. 74 (1980), 189–197.10.1007/BF01197757Google Scholar
Philipp, W. and Stout, W. F.. Almost sure invariance principle for partial sums of weakly dependent random variables. Mem. Amer. Math. Soc. 161 (1975), iv+140pp.Google Scholar
Pitman, J. W.. Uniform rates of convergence for Markov chain transition probabilities. Z. Wahrscheinlichkeitstheor. verw. Geb. 29 (1974), 193–227.10.1007/BF00536280Google Scholar
Rio, E.. Théorie asymptotique des processus aléatoires faiblement dépendants. Math. Appl. (Berlin) 31 (2000), x+169pp.Google Scholar
Sakhanenko, A. I.. Estimates in the invariance principle in terms of truncated power moments. Sib. Math. J. 47 (2006), 1355–1371.10.1007/s11202-006-0119-1Google Scholar
Sarig, O.. Subexponential decay of correlations. Invent. Math. 150 (2002), 629–653.10.1007/s00222-002-0248-5Google Scholar
Young, L.-S.. Statistical properties of dynamical systems with some hyperbolicity. Ann. of Math. (2) 147 (1998), 585–650.10.2307/120960Google Scholar
Young, L.-S.. Recurrence times and rates of mixing. Israel J. Math. 110 (1999), 153–188.Google Scholar
Zaitsev, A. Yu.. Multidimensional version of the results of Komlós, Major and Tusnády for vectors with finite exponential moments. ESAIM Probab. Stat. 2 (1998), 41–108.10.1051/ps:1998103Google Scholar
Zweimüller, R.. Ergodic structure and invariant densities of non-Markovian interval maps with indifferent fixed points. Nonlinearity 11 (1998), 1263–1276.Google Scholar
Zweimüller, R.. Measure preserving transformations similar to Markov shifts. Israel J. Math. 173 (2009), 421–443.Google Scholar