Article contents
Rationality of dynamical canonical height
Published online by Cambridge University Press: 18 January 2018
Abstract
We present a dynamical proof of the well-known fact that the Néron–Tate canonical height (and its local counterpart) takes rational values at points of an elliptic curve over a function field 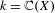 $k=\mathbb{C}(X)$, where
$k=\mathbb{C}(X)$, where 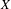 $X$ is a curve. More generally, we investigate the mechanism by which the local canonical height for a map
$X$ is a curve. More generally, we investigate the mechanism by which the local canonical height for a map 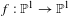 $f:\mathbb{P}^{1}\rightarrow \mathbb{P}^{1}$ defined over a function field
$f:\mathbb{P}^{1}\rightarrow \mathbb{P}^{1}$ defined over a function field 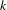 $k$ can take irrational values (at points in a local completion of
$k$ can take irrational values (at points in a local completion of  $k$), providing examples in all degrees
$k$), providing examples in all degrees 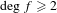 $\deg f\geq 2$. Building on Kiwi’s classification of non-archimedean Julia sets for quadratic maps [Puiseux series dynamics of quadratic rational maps. Israel J. Math.201 (2014), 631–700], we give a complete answer in degree 2 characterizing the existence of points with irrational local canonical heights. As an application we prove that if the heights
$\deg f\geq 2$. Building on Kiwi’s classification of non-archimedean Julia sets for quadratic maps [Puiseux series dynamics of quadratic rational maps. Israel J. Math.201 (2014), 631–700], we give a complete answer in degree 2 characterizing the existence of points with irrational local canonical heights. As an application we prove that if the heights 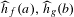 $\widehat{h}_{f}(a),\widehat{h}_{g}(b)$ are rational and positive, for maps
$\widehat{h}_{f}(a),\widehat{h}_{g}(b)$ are rational and positive, for maps 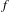 $f$ and
$f$ and  $g$ of multiplicatively independent degrees and points
$g$ of multiplicatively independent degrees and points 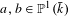 $a,b\in \mathbb{P}^{1}(\bar{k})$, then the orbits
$a,b\in \mathbb{P}^{1}(\bar{k})$, then the orbits  $\{f^{n}(a)\}_{n\geq 0}$ and
$\{f^{n}(a)\}_{n\geq 0}$ and 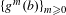 $\{g^{m}(b)\}_{m\geq 0}$ intersect in at most finitely many points, complementing the results of Ghioca et al [Intersections of polynomials orbits, and a dynamical Mordell–Lang conjecture. Invent. Math.171 (2) (2008), 463–483].
$\{g^{m}(b)\}_{m\geq 0}$ intersect in at most finitely many points, complementing the results of Ghioca et al [Intersections of polynomials orbits, and a dynamical Mordell–Lang conjecture. Invent. Math.171 (2) (2008), 463–483].
Information
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2018
References
- 5
- Cited by

