Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-31T05:20:03.664Z Has data issue: false hasContentIssue false
  • English
  • Français

Ratner’s property and mild mixing for smooth flows on surfaces

Published online by Cambridge University Press:  25 August 2015

ADAM KANIGOWSKI  and
JOANNA KUŁAGA-PRZYMUS
ADAM KANIGOWSKI
Affiliation:
Institute of Mathematics, Polish Acadamy of Sciences, Śniadeckich 8, 00-956 Warszawa, Poland email adkanigowski@gmail.com
JOANNA KUŁAGA-PRZYMUS
Affiliation:
Institute of Mathematics, Polish Acadamy of Sciences, Śniadeckich 8, 00-956 Warszawa, Poland email adkanigowski@gmail.com Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, Chopina 12/18, 87-100 Toruń, Poland email joanna.kulaga@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 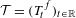${\mathcal{T}}=(T_{t}^{f})_{t\in \mathbb{R}}$ be a special flow built over an IET 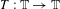$T:\mathbb{T}\rightarrow \mathbb{T}$ of bounded type, under a roof function 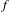$f$ with symmetric logarithmic singularities at a subset of discontinuities of $T$ . We show that 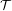${\mathcal{T}}$ satisfies the so-called switchable Ratner’s property which was introduced in Fayad and Kanigowski [On multiple mixing for a class of conservative surface flows. Invent. Math. to appear]. A consequence of this fact is that such flows are mildly mixing (before, they were only known to be weakly mixing [Ulcigrai. Weak mixing for logarithmic flows over interval exchange transformations.J. Mod. Dynam.3 (2009), 35–49] and not mixing [Ulcigrai. Absence of mixing in area-preserving flows on surfaces. Ann. of Math. (2) 173 (2011), 1743–1778]). Thus, on each compact, connected, orientable surface of genus greater than one there exist flows that are mildly mixing and not mixing.

Information

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 8 , December 2016 , pp. 2512 - 2537
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arnol′d, V. I.. Topological and ergodic properties of closed 1-forms with incommensurable periods. Funktsional. Anal. Prilozhen. 25 (1991), 81–90.Google Scholar
Boshernitzan, M. D.. Rank two interval exchange transformations. Ergod. Th. & Dynam. Sys. 8 (1988), 379–394.CrossRefGoogle Scholar
Conze, J.-P. and Fra̧czek, K.. Cocycles over interval exchange transformations and multivalued Hamiltonian flows. Adv. Math. 226 (2011), 4373–4428.CrossRefGoogle Scholar
Fayad, B. and Kanigowski, A.. On multiple mixing for a class of conservative surface flows. Invent. Math. to appear.Google Scholar
Frączek, K. and Lemańczyk, M.. A class of special flows over irrational rotations which is disjoint from mixing flows. Ergod. Th. & Dynam. Sys. 24 (2004), 1083–1095.CrossRefGoogle Scholar
Frączek, K. and Lemańczyk, M.. On mild mixing of special flows over irrational rotations under piecewise smooth functions. Ergod. Th. & Dynam. Sys. 26 (2006), 719–738.CrossRefGoogle Scholar
Frączek, K. and Lemańczyk, M.. Ratner’s property and mild mixing for special flows over two-dimensional rotations. J. Mod. Dynam. 4 (2010), 609–635.Google Scholar
Frączek, K., Lemańczyk, M. and Lesigne, E.. Mild mixing property for special flows under piecewise constant functions. Discrete Contin. Dynam. Sys. 19 (2007), 691–710.CrossRefGoogle Scholar
Frączek, K. and Ulcigrai, C.. Ergodic properties of infinite extensions of area-preserving flows. Math. Ann. 354 (2012), 1289–1367.Google Scholar
Furstenberg, H. and Weiss, B.. The finite multipliers of infinite ergodic transformations. The Structure of Attractors in Dynamical Systems (Proc. Conf., North Dakota State University, Fargo, ND, 1977) (Lecture Notes in Mathematics, 668) . Springer, Berlin, 1978, pp. 127–132.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Hubert, P., Marchese, L. and Ulcigrai, C.. Lagrange Spectra in Teichmüller Dynamics via renormalization. Geom. Funct. Anal. 25(1) (2015), 180–225.Google Scholar
Kanigowski, A.. Ratner’s property for special flows over irrational rotations under functions of bounded variation. Ergod. Th. & Dynam. Sys. 35(3) (2015), 915–934.Google Scholar
Kanigowski, A.. Ratner’s property for special flows over irrational rotations under functions of bounded variation. ii. Colloq. Math. 136(1) (2014), 125–147.Google Scholar
Katok, A. and Thouvenot, J.-P.. Spectral properties and combinatorial constructions in ergodic theory. Handbook of Dynamical Systems, Vol. 1B. Elsevier, Amsterdam, 2006, pp. 649–743.Google Scholar
Keane, M.. Interval exchange transformations. Math. Z. 141 (1975), 25–31.Google Scholar
Kim, D. H. and Marmi, S.. Bounded type interval exchange maps. Nonlinearity 27 (2014), 637–645.Google Scholar
Kochergin, A. V.. The absence of mixing in special flows over a rotation of the circle and in flows on a two-dimensional torus. Dokl. Akad. Nauk SSSR 205 (1972), 515–518.Google Scholar
Kochergin, A. V.. Mixing in special flows over a rearrangement of segments and in smooth flows on surfaces. Mat. Sb. (N.S.) 96(138) (1975), 471–502, 504.Google Scholar
Kochergin, A. V.. Nondegenerate saddles, and the absence of mixing. Mat. Zametki 19 (1976), 453–468.Google Scholar
Kułaga, J.. On the self-similarity problem for smooth flows on orientable surfaces. Ergod. Th. & Dynam. Sys. 32 (2012), 1615–1660.Google Scholar
Levitt, G.. Pantalons et feuilletages des surfaces. Topology 21 (1982), 9–33.Google Scholar
Marmi, S., Moussa, P. and Yoccoz, J.-C.. The cohomological equation for Roth-type interval exchange maps. J. Amer. Math. Soc. 18 (2005), 823–872 (electronic).Google Scholar
Mayer, A.. Trajectories on the closed orientable surfaces. Rec. Math. [Mat. Sbornik] N.S. 12(54) (1943), 71–84.Google Scholar
von Neumann, J.. Zur Operatorenmethode in der klassischen Mechanik. Ann. of Math. (2) 33 (1932), 587–642.CrossRefGoogle Scholar
Novikov, S. P.. The Hamiltonian formalism and a multivalued analogue of Morse theory. Uspekhi Mat. Nauk 37 (1982), 3–49, 248.Google Scholar
Ratner, M.. Horocycle flows, joinings and rigidity of products. Ann. of Math. (2) 118 (1983), 277–313.Google Scholar
Rauzy, G.. Échanges d’intervalles et transformations induites. Acta Arith. 34 (1979), 315–328.Google Scholar
Sinaĭ, Y. G. and Khanin, K. M.. Mixing of some classes of special flows over rotations of the circle. Funktsional. Anal. Prilozhen. 26 (1992), 1–21.Google Scholar
Sinaĭ, Y. G. and Ulcigrai, C.. Weak mixing in interval exchange transformations of periodic type. Lett. Math. Phys. 74 (2005), 111–133.Google Scholar
Thouvenot, J.-P.. Some properties and applications of joinings in ergodic theory. Ergodic Theory and its Connections with Harmonic Analysis (Alexandria, 1993) (London Mathematical Society Lecture Notes Series, 205) . Cambridge University Press, Cambridge, 1995, pp. 207–235.Google Scholar
Ulcigrai, C.. Weak mixing for logarithmic flows over interval exchange transformations. J. Mod. Dynam. 3 (2009), 35–49.CrossRefGoogle Scholar
Ulcigrai, C.. Absence of mixing in area-preserving flows on surfaces. Ann. of Math. (2) 173 (2011), 1743–1778.Google Scholar
Veech, W. A.. Projective Swiss cheeses and uniquely ergodic interval exchange transformations. Ergodic Theory and Dynamical Systems, I (College Park, MD, 1979–80) (Progress in Mathematics, 10) . Birkhäuser, Boston, MA, 1981, pp. 113–193.Google Scholar
Viana, M.. Dynamics of interval exchange transformations and teichmüller flows. Lecture Notes. Available from http://w3.impa.br/viana.Google Scholar
Witte, D.. Rigidity of some translations on homogeneous spaces. Invent. Math. 81 (1985), 1–27.Google Scholar
Yoccoz, J.-C.. Continued fraction algorithms for interval exchange maps: an introduction. Frontiers in Number Theory, Physics, and Geometry. I. Springer, Berlin, 2006, pp. 401–435.Google Scholar
Yoccoz, J.-C.. Interval exchange maps and translation surfaces. Homogeneous Flows, Moduli Spaces and Arithmetic (Clay Mathematics Monographs, 10) . American Mathematical Society, Providence, RI, 2010, pp. 1–69.Google Scholar
Zorich, A.. Hamiltonian flows of multivalued hamiltonians on closed orientable surfaces. 1994, unpublished.Google Scholar
Zorich, A.. Finite Gauss measure on the space of interval exchange transformations. Lyapunov exponents. Ann. Inst. Fourier (Grenoble) 46 (1996), 325–370.Google Scholar
Zorich, A.. How do the leaves of a closed 1-form wind around a surface? Pseudoperiodic Topology (American Mathematical Society Translations, Series 2, 197) . American Mathematical Society, Providence, RI, 1999, pp. 135–178.Google Scholar