Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T05:38:03.865Z Has data issue: false hasContentIssue false
  • English
  • Français

Relativization of sensitivity in minimal systems

Part of: Topological dynamics Connections with other structures, applications Ergodic theory

Published online by Cambridge University Press:  27 December 2018

TAO YU  and
XIAOMIN ZHOU Open the ORCID record for XIAOMIN ZHOU [Opens in a new window]
TAO YU
Affiliation:
Shanghai Center for Mathematical Sciences, Fudan University, Shanghai, 200433, PR China email ytnuo@mail.ustc.edu.cn
XIAOMIN ZHOU
Affiliation:
Department of Mathematics, Huazhong University of Science and Technology, Wuhan, Hubei, 430074, PR China email zxm12@mail.ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 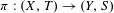$\unicode[STIX]{x1D70B}:(X,T)\rightarrow (Y,S)$ be an extension between minimal systems; we consider its relative sensitivity. We obtain that $\unicode[STIX]{x1D70B}$ is relatively $n$-sensitive if and only if the relative $n$-regionally proximal relation contains a point whose coordinates are distinct; and the structure of $\unicode[STIX]{x1D70B}$ which is relatively $n$-sensitive but not relatively 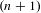$(n+1)$-sensitive is determined. Let 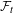${\mathcal{F}}_{t}$ be the families consisting of thick sets. We introduce notions of relative block 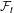${\mathcal{F}}_{t}$-sensitivity and relatively strong 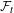${\mathcal{F}}_{t}$-sensitivity. Let 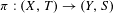$\unicode[STIX]{x1D70B}:(X,T)\rightarrow (Y,S)$ be an extension between minimal systems. Then the following Auslander–Yorke type dichotomy theorems are obtained: (1) $\unicode[STIX]{x1D70B}$ is either relatively block 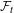${\mathcal{F}}_{t}$-sensitive or 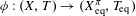$\unicode[STIX]{x1D719}:(X,T)\rightarrow (X_{\text{eq}}^{\unicode[STIX]{x1D70B}},T_{\text{eq}})$ is a proximal extension where 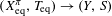$(X_{\text{eq}}^{\unicode[STIX]{x1D70B}},T_{\text{eq}})\rightarrow (Y,S)$ is the maximal equicontinuous factor of $\unicode[STIX]{x1D70B}$. (2) $\unicode[STIX]{x1D70B}$ is either relatively strongly 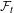${\mathcal{F}}_{t}$-sensitive or 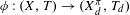$\unicode[STIX]{x1D719}:(X,T)\rightarrow (X_{d}^{\unicode[STIX]{x1D70B}},T_{d})$ is a proximal extension where 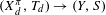$(X_{d}^{\unicode[STIX]{x1D70B}},T_{d})\rightarrow (Y,S)$ is the maximal distal factor of $\unicode[STIX]{x1D70B}$.

Keywords

relative sensitivityminimalityequicontinuous factordistal factor

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Secondary: 37A05: Measure-preserving transformations 54H20: Topological dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 6 , June 2020 , pp. 1715 - 1728
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, J.. Minimal Flows and Their Extensions (North-Holland Mathematics Studies 153). Elsevier, Amsterdam, 1988.Google Scholar
Auslander, J. and Horelick, B.. Regular minimal sets. II. The proximally equicontinuous case. Compos. Math. 22 (1970), 203–214.Google Scholar
Auslander, J. and Yorke, J. A.. Interval maps, factors of maps, and chaos. Tôhoku Math. J. (2) 32(2) (1980), 177–188.Google Scholar
Ellis, R., Glasner, S. and Shapiro, L.. Proximal-isometric flows. Adv. Math. 17 (1975), 213–260.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (M. B. Porter Lectures). Princeton University Press, Princeton, NJ, 1981.Google Scholar
García-Ramos, F., Li, J. and Zhang, R.. When is a dynamical system mean sensitive. Preprint, 2017,arXiv:1708.01987. Ergod. Th. & Dynam. Sys. to appear.Google Scholar
Glasner, E. and Weiss, B.. Sensitive dependence on initial conditions. Nonlinearity 6(6) (1993), 1067–1075.Google Scholar
Huang, W., Khilko, D., Kolyada, S. and Zhang, G.. Dynamical compactness and sensitivity. J. Differential Equation 260(9) (2016), 6800–6827.Google Scholar
Huang, W., Kolyada, S. and Zhang, G.. Analogues of Auslander-Yorke theorems for multi-sensitivity. Ergod. Th. & Dynam. Sys. 38(2) (2018), 651–665.Google Scholar
Huang, W., Lu, P. and Ye, X.. Measure-theoretical sensitivity and equicontinuity. Israel J. Math. 183 (2011), 233–283.Google Scholar
Li, J.. Measure-theoretic sensitivity via finite partitions. Nonlinearity 29(7) (2016), 2133–2144.Google Scholar
Li, J., Tu, S. and Ye, X.. Mean equicontinuity and mean sensitivity. Ergod. Th. & Dynam. Sys. 35(8) (2015), 2587–2612.Google Scholar
Liu, K. and Zhou, X.. Auslander-Yorkes type dichotomy theorems for stronger version $r$-sensitivity, preprint.Google Scholar
Maass, A. and Shao, S.. Structure of bounded topological-sequence-entropy minimal systems. J. Lond. Math. Soc. (2) 76(3) (2007), 702–718.Google Scholar
McMahon, D. C.. Relativized weak disjointness and relatively invariant measures. Trans. Amer. Math. Soc. 236 (1978), 225–237.Google Scholar
Subrahmonian Moothathu, T. K.. Stronger forms of sensitivity for dynamical systems. Nonlinearity 20(9) (2007), 2115–2126.Google Scholar
Ruelle, D.. Dynamical Systems with Turbulent Behavior, Mathematical Problems in Theoretical Physics (Proc. Internat. Conf., Univ. Rome, Rome, 1977) (Lecture Notes in Physics, 80). Springer, Berlin, 1978, pp. 341–360.Google Scholar
Shao, S., Ye, X. and Zhang, R.. Sensitivity and regionally proximal relation in minimal systems. Sci. China 51(6) (2008), 987–994.Google Scholar
de Vries, J.. Elements of Topological Dynamics. Kluwer Academic Publishers, Dordrecht, 1993.Google Scholar
Xiong, J.. Chaos in topological transitive systems. Sci. China 48(7) (2005), 929–939.Google Scholar
Ye, X. and Yu, T.. Sensitivity, proximal extension and high order almost automorphy. Trans. Amer. Math. Soc. 370(5) (2018), 3639–3662.Google Scholar
Ye, X. and Zhang, R.. On sensitive sets in topological dynamics. Nonlinearity 21(7) (2008), 1601–1620.Google Scholar
Yu, T.. Measurable sensitivity via Furstenberg families. Discrete Contin. Dyn. Syst. 37(8) (2017), 4543–4563.Google Scholar
Zhang, G.. Relativization of complexity and sensitivity. Ergod. Th. & Dynam. Sys. 27(4) (2007), 1349–1371.Google Scholar
Zou, Y.. Stronger version sensitivity, almost finite to one extension and maximal pattern entropy. Commun. Math. Stat. 5(2) (2017), 123–139.Google Scholar