Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T01:37:06.029Z Has data issue: false hasContentIssue false
  • English
  • Français

Schmidt’s game, fractals, and orbits of toral endomorphisms

Published online by Cambridge University Press:  05 August 2010

RYAN BRODERICK ,
LIOR FISHMAN  and
DMITRY KLEINBOCK
RYAN BRODERICK
Affiliation:
Department of Mathematics, Brandeis University, Waltham, MA 02454-9110, USA (email: ryanb@brandeis.edu, lfishman@brandeis.edu, kleinboc@brandeis.edu)
LIOR FISHMAN
Affiliation:
Department of Mathematics, Brandeis University, Waltham, MA 02454-9110, USA (email: ryanb@brandeis.edu, lfishman@brandeis.edu, kleinboc@brandeis.edu)
DMITRY KLEINBOCK
Affiliation:
Department of Mathematics, Brandeis University, Waltham, MA 02454-9110, USA (email: ryanb@brandeis.edu, lfishman@brandeis.edu, kleinboc@brandeis.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

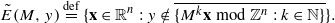Given an integer matrix M∈GLn(ℝ) and a point y∈ℝn/ℤn, consider the set S. G. Dani showed in 1988 that whenever M is semisimple and y∈ℚn/ℤn, the set 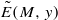has full Hausdorff dimension. In this paper we strengthen this result, extending it to arbitrary M∈GLn(ℝ)∩Mn×n(ℤ) and y∈ℝn/ℤn, and in fact replacing the sequence of powers of M by any lacunary sequence of (not necessarily integer) m×n matrices. Furthermore, we show that sets of the form 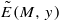and their generalizations always intersect with ‘sufficiently regular’ fractal subsets of ℝn. As an application, we give an alternative proof of a recent result [M. Einsiedler and J. Tseng. Badly approximable systems of affine forms, fractals, and Schmidt games. Preprint, arXiv:0912.2445] on badly approximable systems of affine forms.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 31 , Issue 4 , August 2011 , pp. 1095 - 1107
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Broderick, R., Bugeaud, Y., Fishman, L., Kleinbock, D. and Weiss, B.. Schmidt’s game, fractals, and numbers normal to no base. Math. Res. Lett. 17(2) (2010), 309–323.CrossRefGoogle Scholar
[2]Bugeaud, Y., Harrap, S., Kristensen, S. and Velani, S.. On shrinking targets for ℤm actions on tori. Mathematika, to appear.Google Scholar
[3]Bugeaud, Y. and Laurent, M.. On exponents of homogeneous and inhomogeneous Diophantine approximation. Moscow Math. J. 5(4) (2005), 747–766, 972.CrossRefGoogle Scholar
[4]Cassels, J. W. S.. An Introduction to Diophantine Approximation. Cambridge University Press, Cambridge, UK, 1957.Google Scholar
[5]Dani, S. G.. On orbits of endomorphisms of tori and the Schmidt game. Ergod. Th. & Dynam. Sys. 8 (1988), 523–529.Google Scholar
[6]de Mathan, B.. Numbers contravening a condition in density modulo 1. Acta Math. Acad. Sci. Hungar. 36 (1980), 237–241.CrossRefGoogle Scholar
[7]Einsiedler, M. and Tseng, J.. Badly approximable systems of affine forms, fractals, and Schmidt games. Preprint, arXiv:0912.2445.Google Scholar
[8]Esdahl-Schou, R. and Kristensen, S.. On badly approximable complex numbers. Glasg. Math. J. 52 (2010), 349–355.CrossRefGoogle Scholar
[9]Falconer, K.. Fractal Geometry. Mathematical Foundations and Applications. John Wiley, Hoboken, NJ, 2003.CrossRefGoogle Scholar
[10]Färm, D.. Simultaneously non-dense orbits under different expanding maps. Preprint, arXiv:0904.4365v1.Google Scholar
[11]Färm, D., Persson, T. and Schmeling, J.. Dimension of countable intersections of some sets arising in expansions in non-integer bases. Fund. Math., to appear.Google Scholar
[12]Fishman, L.. Schmidt’s game on fractals. Israel J. Math. 171(1) (2009), 77–92.CrossRefGoogle Scholar
[13]Fishman, L.. Schmidt’s game, badly approximable matrices and fractals. J. Number Theory 129(9) (2009), 2133–2153.CrossRefGoogle Scholar
[14]Kleinbock, D.. Nondense orbits of flows on homogeneous spaces. Ergod. Th. & Dynam. Sys. 18 (1998), 373–396.Google Scholar
[15]Kleinbock, D.. Badly approximable systems of affine forms. J. Number Theory 79(1) (1999), 83–102.CrossRefGoogle Scholar
[16]Kleinbock, D., Lindenstrauss, E. and Weiss, B.. On fractal measures and Diophantine approximation. Selecta Math. 10 (2004), 479–523.CrossRefGoogle Scholar
[17]Kleinbock, D. and Weiss, B.. Badly approximable vectors on fractals. Israel J. Math. 149 (2005), 137–170.CrossRefGoogle Scholar
[18]Kleinbock, D. and Weiss, B.. Modified Schmidt games and Diophantine approximation with weights. Adv. Math. 223(4) (2010), 1276–1298.CrossRefGoogle Scholar
[19]Kristensen, S., Thorn, R. and Velani, S. L.. Diophantine approximation and badly approximable sets. Adv. Math. 203 (2006), 132–169.CrossRefGoogle Scholar
[20]Kronecker, L.. Zwei Sätze über Gleichungen mit ganzzahligen Coefficienten. J. Reine Angew. Math. 53 (1857), 173–175; see also L. Kronecker. Werke, Vol. 1. Chelsea Publishing Co., New York, 1968, pp. 103–108.Google Scholar
[21]McMullen, C.. Winning sets, quasiconformal maps and Diophantine approximation, Geom. Funct. Anal., to appear.Google Scholar
[22]Moshchevitin, N. G.. A note on badly approximable affine forms and winning sets. Preprint, arXiv:0812.3998v2.Google Scholar
[23]Pollington, A. D.. On nowhere dense ∂-sets. Groupe de travail d’analyse ultramétrique 10(2) (1982–1983), Exp. No. 22, 2 pp.Google Scholar
[24]Pollington, A. D.. On the density of the sequence {η kξ}. Illinois J. Math. 23(4) (1979), 511–515.Google Scholar
[25]Pollington, A. D. and Velani, S. L.. Metric Diophantine approximation and ‘absolutely friendly’ measures. Selecta Math. 11 (2005), 297–307.CrossRefGoogle Scholar
[26]Schmidt, W. M.. On badly approximable numbers and certain games. Trans. Amer. Math. Soc. 123 (1966), 27–50.CrossRefGoogle Scholar
[27]Schmidt, W. M.. Badly approximable systems of linear forms. J. Number Theory 1 (1969), 139–154.CrossRefGoogle Scholar
[28]Schmidt, W. M.. Diophantine Approximation (Lecture Notes in Mathematics, 785). Springer, Berlin, 1980.Google Scholar
[29]Stratmann, B. and Urbanski, M.. Diophantine extremality of the Patterson measure. Math. Proc. Cambridge Philos. Soc. 140 (2006), 297–304.CrossRefGoogle Scholar
[30]Tseng, J.. Schmidt games and Markov partitions. Nonlinearity 22(3) (2009), 525–543.Google Scholar
[31]Tseng, J.. Badly approximable affine forms and Schmidt games. J. Number Theory 129 (2009), 3020–3025.CrossRefGoogle Scholar
[32]Urbanski, M.. Diophantine approximation of self-conformal measures. J. Number Theory 110 (2005), 219–235.CrossRefGoogle Scholar