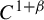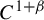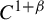Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Obata, Davi
2023.
Open sets of partially hyperbolic skew products having a unique SRB measure.
Advances in Mathematics,
Vol. 427,
Issue. ,
p.
109136.
Brown, Aaron
Hertz, Federico Rodriguez
and
Wang, Zhiren
2023.
Smooth ergodic theory of $ \mathbb {Z}^d $-actions.
Journal of Modern Dynamics,
Vol. 19,
Issue. 0,
p.
455.
Gogolev, Andrey
and
Shi, Yi
2023.
Joint integrability and spectral rigidity for Anosov diffeomorphisms.
Proceedings of the London Mathematical Society,
Vol. 127,
Issue. 6,
p.
1693.
Crovisier, Sylvain
Obata, Davi
and
Poletti, Mauricio
2024.
Uniqueness of u-Gibbs Measures for Hyperbolic Skew Products on $$\mathbb {T}^4$$.
Communications in Mathematical Physics,
Vol. 405,
Issue. 9,
Mongez, Juan
and
Pacifico, Maria
2024.
Finite measures of maximal entropy for an open set of partially hyperbolic diffeomorphisms.
Transactions of the American Mathematical Society,
Mongez, Juan Carlos
and
Pacifico, Maria José
2025.
Robustness and uniqueness of equilibrium states for certain partially hyperbolic systems*
.
Nonlinearity,
Vol. 38,
Issue. 3,
p.
035020.
Yongluo, Cao
and
Yun, Zhao
2025.
Dimension theory in non-conformal smooth systems.
SCIENTIA SINICA Mathematica,
Zhang, Jinhua
2025.
Entropy properties of mostly expanding partially hyperbolic diffeomorphisms.
Mathematische Annalen,
Vol. 393,
Issue. 1,
p.
953.
Liao, Gang
and
Wang, Shirou
2025.
Entropy Formula of Folding Type for $$C^{1+\alpha }$$ Maps.
Communications in Mathematical Physics,
Vol. 406,
Issue. 12,
Micena, Fernando
Moore, Ryo
Rodriguez Hertz, Jana
and
Ures, Raul
2025.
Measures of maximal entropy that are SRB.
Advances in Mathematics,
Vol. 482,
Issue. ,
p.
110630.
LIANG, CHAO
SAGHIN, RADU
YANG, FAN
and
YANG, JIAGANG
2025.
Shub’s example revisited.
Ergodic Theory and Dynamical Systems,
Vol. 45,
Issue. 3,
p.
894.
Burguet, David
and
Yang, Dawei
2025.
SRB Measures for Mostly Expanding Partially Hyperbolic Diffeomorphisms via the Variational Approach.
International Mathematics Research Notices,
Vol. 2025,
Issue. 6,
SAGHIN, RADU
2025.
On invariant holonomies between centers.
Ergodic Theory and Dynamical Systems,
Vol. 45,
Issue. 1,
p.
274.