Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lind, Douglas
1992.
Matrices of Perron numbers.
Journal of Number Theory,
Vol. 40,
Issue. 2,
p.
211.
Angelis, Valerio De
1994.
Polynomial beta functions.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 3,
p.
453.

 ⊂
⊂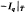 equals that of
equals that of 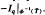 . Applying this to Bernoulli shifts and using finiteness conditions on Perron numbers, we have the following. If the probability vector
. Applying this to Bernoulli shifts and using finiteness conditions on Perron numbers, we have the following. If the probability vector 