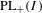Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Elliott, L.
Jonušas, J.
Mitchell, J.D.
Péresse, Y.
and
Pinsker, M.
2023.
Polish topologies on endomorphism monoids of relational structures.
Advances in Mathematics,
Vol. 431,
Issue. ,
p.
109214.
Elliott, L.
Jonušas, J.
Mesyan, Z.
Mitchell, J.
Morayne, M.
and
Péresse, Y.
2023.
Automatic continuity, unique Polish topologies, and Zariski topologies on monoids and clones.
Transactions of the American Mathematical Society,